Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

7005

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.15 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 156 7 8 9 10 11 12 13 14 15 > Следующая >>>

система:

1		1
	2	4

	1	5

	A B 2
		1
2 A 4B C
		9
A 5B 5C
0	2	1
	1
1			0
5	9		0

решим еѐ методом Гаусса.

1	0	2	1		1	0	2
6		5			6		5
6	1	5		0	6	1	5	.
6	5	11		0 0		6	6

Здесь от 2-й строки отняли удвоенную 1-ю и от 3-й 1-ю, а затем от 3-й строки 2-ю. Основная матрица системы стала треугольной, и С находится сразу же: С 1. Тогда 6B 1 5 и тогда B 1. Из 1-го уравнения тогда уже получается A 1.

Значит, исходный интеграл распадается на сумму 3 интегралов:

1	1	1	1	1		1					10 ln				10			1		1
1		1		1																1
		dx		dx				dx = ln		x 5		x 1								=


	x 5		x 1		(x	1)	2										x 1
																				0

0		0		0
0		0		0		1							1			8			1
						1							1			8			1
(ln 4 ln 5)			(ln 2 ln 1)				1		= ln 4 ln 5 ln 2					= ln						.
(ln 4 ln 5)			(ln 2 ln 1)				1		= ln 4 ln 5 ln 2					= ln						.
						2							2			5			2

Ответ. ln 85 12 .

1 1 4 x

Задача 3. Вычислить интеграл dx .

0 x

При этом осуществляется повторение темы «интегрирование иррациональностей».

Решение. НОК(2,4) = 4, поэтому замена t 4 x . При такой замене


x t 4 ,				dx 4t 3dt ,							x t 2 .			x (0,1) t (0,1) .
1 1 4				1				1 t						1	1	4		1	4		1
			x
			x
					dx =					4t 3dt		= 4 (1 t)tdt			= 4 (t t 2 )dt =		t 2			t 3	=
								t	2							2			3
		x							2
0				0										0	0			0			0
0				0										0	0			0			0
2	4		=			10	.		Ответ.			10	.
2	3		=	3			.		Ответ.			3	.
	3			3								3

cos4 x

Задача 4. Вычислить интеграл 3 sin 2 x dx .

При этом осуществляется повторение темы «интегрирование тригонометрических функций».

Решение. Суммарная степень чѐтна, поэтому применяется замена

, cos x

t tgx , тогда

dt ,

sin x

t 2 1

1 t 2

t tg0 0

t tg

Пересчитаем границы. x 0

, x

3 .

Итак, подставим всѐ это в интеграл.

										t 2
	3	2					3												3		t	2	(t	2	1)	2			1
	3	2					3			2 1									3			2		2		2
		sin x		dx =					t	2 1					1		dt =													dt =
		4		dx =						1				2		1	dt =			t	2	1			1		t	2	1	dt =
0		cos	x				0			1			t						0	t		1			1		t		1
0		cos	x				0	(t 2 1)2					t						0
								(t 2 1)2
		3					3				3
		3			1		3			3	3					3 3
= t 2 dt =					1	t 3		=		3		=				3 3		= 3 .
= t 2 dt =						t 3		=				=						= 3 .
		0	3				0			3					3
		0					0

Ответ.			3 .

Контрольная работа: 45 минут

1.Подведение под знак дифференциала, преобразования.

2.Интегрирование по частям.

3.Интегрирование рациональных дробей.

4.Интегрирование иррациональностей и тригонометрических функций.

ПРАКТИКА № 8.

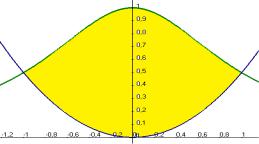
Задача 1. Найти площадь фигуры, ограниченной линиями:

y	x 2	и y		1	.
			2
1	2			x 2 1

Решение. Рассмотрим чертѐж, найдѐм точки пересечения графиков и увидим, какую часть плоскости они ограничивают.

График				y2			1	имеет максимум в точке 0 и проходит выше, чем

						x 2 1
						x 2 1
y			x 2	, у	которой, напротив, там				минимум. Точки перечечения
y				, у	которой, напротив, там				минимум. Точки перечечения
1		2
		2
	1					1
1,		,		1,			. Все функции в		интеграле чѐтные, фигура
1,		,		1,			. Все функции в		интеграле чѐтные, фигура
	2					2

симметрична, можно вычислить площадь правой половины и удвоить:

1	1		x2			1	1		x2			1	x3	1


					=									=
S	2	1	2	dx		2	2	1	2	dx	= 2arctgx	0 2	6

1 x						0 x								0

			1				1			1
2		0	2		0 =			. Ответ.			.
2		0	2		0 =			. Ответ.			.
	4			6		2	3		2	3

Задача 2. Найти площадь области, ограниченной линиями

y x 2 , y x, x 1

Решение.

1	1		3	1			2	1
1	1		3	1			2	1
x 2 (x) dx = x 2 x dx =		x				x		=	1	1	=	5	.
x 2 (x) dx = x 2 x dx =								=			=		.
0	0	3		0	2			0	3	2		6
0	0			0				0

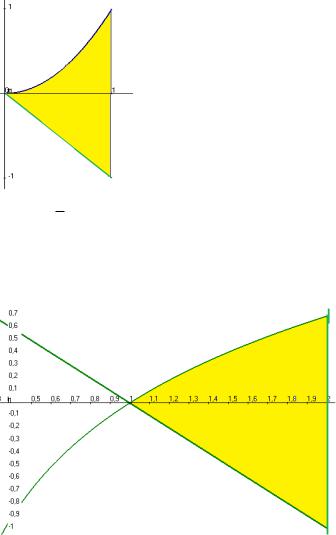
Чертѐж:

Ответ. 56 .

Задача 3. Найти площадь фигуры, ограниченной линиями:x 2, y ln x, y 1 x .

Решение. Чертѐж:

2	2	2	x 2	2


ln x (1 x) dx	= ln x x 1 dx = ln xdx +			x	12

			2

1	1	1		1

для раскрытия 1-го слагаемого, вспомним пример из лекйиц на интегрирование по частям, там делали именно этим методом.

Если u ln x						, u						1	,		v 1,			v x то:
Если u ln x						, u							,		v 1,			v x то:
												x
2			x 2			2					12							2	x 2	2		12
						2														2

ln xdx +							x					=			x ln x		12 dx +			x			=

			2																2


1						1												1		1
1						1	x 2			2								1		1
	2	x		2										2							4		1


x ln x	1			1 +							x			1		= 2 ln 2 2(2 1)								=
x ln x											x					= 2 ln 2 2(2 1)								=
						2				1											2		2
						2															2		2
					3										1
2 ln 2 2					3	= 2 ln 2									1	.
2 ln 2 2						= 2 ln 2										.
			2												2
Ответ.		2 ln 2						1	.
Ответ.		2 ln 2							.
						2

Задача 4. Найти объѐм, получающийся при вращении кривой y x ,

при условии что

x [0, a] .

Решение. V

f 2 (x)dx =

2 dx = xdx

Ответ. a 2 .

Замечание. Эта задача может быть интерпретирована физическим примером: сколько воды может поместиться в эллиптический параболоид. Ведь если график корня повернуть на 90 градусов, это парабола.

Задача 5. С помощью основной формулы объѐмов тел вращения,

доказать формулу объѐма конуса V 13 R 2 h .

Решение. Для удобства применения основной формулы, повернѐм конус на 90 градусов, так, чтобы высота лежала на оси 0x .

На чертеже видно, что два катета имеют длины R и h . Тогда отрезок, вращением которого образована боковая поверхность конуса,

находится на прямой y f (x)

x .

(x)dx =

x dx

R 2 h = 1 R 2 h . 1 3 3

Ответ: формула доказана.


Задача 6. Найти длину явно заданной кривой:																													y					x3 , x (0,1) .
												b
Решение. Формула L															1 ( f (x))2 dx .
												a
									3				3													1
	f x 32									x 12																1				9
					f											x . Тогда							L				1			9		xdx =
					f				2			2				x . Тогда							L				1		4			xdx =
									2			2														0			4
																										0
		1																	3		1												3
																			3		1												3
4				9			9					4 2					9								8						9
4				9			9					4 2				1	9								8						9
			1			xd		x 1			=							x						=				1						1	=
			1			xd		x 1			=							x						=				1						1	=
9				4			4					9 3					4				0				27						4
		0																			0
					3									3								3		8
	8 13				3				8		13			3				13				3
	8 13								8		13							13
						1	=								1 =											.
	27		4						27		8									27

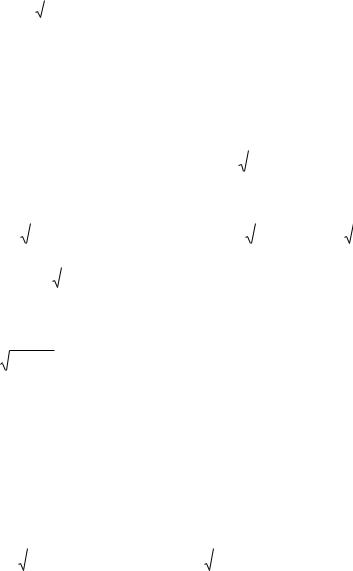
		3 8	.
Ответ.	13
	27

Задача 7. Найти длину 1 витка винтовой линии в пространстве

x R cost, y R sin t, z at t (0,2 )

Решение. В данном случае кривая параметрически задана, в 3-

мерном пространстве. Формула L

(x (t))2 ( y (t))2 (z (t))2 dt .

Производные:

x R sin t, y R cost, z a .

R2 sin 2 t R2 cos2 t a 2 dt

R 2 a 2 dt =

R 2 a 2

1dt

Ответ. 2 R2

a2 .

Замечание. Если была бы не винтовая линия, а окружность, а это было бы при параметре a 0 , то как раз бы и получалось

2	R2 0 2 R длина окружности.
Задача 8. Найти длину дуги х = cos3(2t), y =sin3(2t), 0 t		.
		2

Решение. Производные: x 6 cos2 (2t) sin(2t), y 6 sin 2 (2t) cos(2t).

Для удобства вычислений, сразу вынесем за скобки произведение:

2sin(2t) cos(2t) sin(4t) .
Тогда:	x 3cos(2t) sin(4t) ,	y 3sin(2t) sin(4t).

2		2
2		2
L	(x'(t)) 2 ( y'(t)2 )dt =	3	sin 2 4t(sin 2 2t cos2 2t)dt
0		0


2									2					4			2
2									2					4			2
3				sin 2 4t dt				3		sin 4t		dt	=	3 sin 4tdt 3 ( sin 4t)dt						=
				sin 2 4t dt									=							=

0									0					0
																	4
																4				4		4
3		( cos 4t)			4			3	(cos 4t)		2		=	3	(cos	4	cos0)	3	(cos	4	cos	4	) =
4		( cos 4t)			0		4		(cos 4t)				=	4	(cos	4	cos0)	4	(cos	2	cos	4	) =
4							4							4		4		4		2		4
											4
											4
		3	( 1 1)			3	(1 ( 1))= 3.
	4		( 1 1)			4	(1 ( 1))= 3.
	4					4

Ответ. 3.

Замечание. Если бы не учли знак модуля и не разбили на 2 части, тогда получилось бы неверно, ведь эти части бы не складывались, а взаимно уничтожались:


2						4
	3		2	3
3 sin 4tdt		( cos4t)			(cos		cos0) 0
	4			4		2
0			0

Задача 9. Найти длину кривой, заданной в полярных координатах: r a(1 cos) , (0,2 ) .

Решение. Формула: L (r ( ))2

(r( ))2 d .

r a(1 cos) , r a sin .

a 2 sin 2 a 2 (1 cos)2 d

= a

sin 2 cos2 1 2 cos d

= a

2 2 cos d =

1 cos d

= 2

1 cos d .

дальше будем делать

замену t cos , но

чтобы она задавалась

монотонной функцией и не возникло противоречие в том, что пределы интегрирования (c, c) и 0 в ответе, заранее разбиваем на 2 части и удваиваем интеграл.

t cos , arccost ,

dt , (0, )

t (1, 1) .

1 t 2

1 t

2 2a

1 cos d = 2

1 t

= 2

dt =

1 t 2

1 t

d (1 t

)

d (1 t)

= 4

1 =

dt = 2

= 4

1 t

2 1 t

0 8a .

Ответ. 8a .

Домашнее задание.

Найти длину кривой x 5cos3 t, y 5sin 3 t t (0, ) . Ответ.15.

ПРАКТИКА № 9.

Несобственный интеграл.

Задача 1. Вычислить несобственный интеграл 1 рода e 5 x dx .

5 x

Решение. e

dx =

lim

dx = lim

lim

5 b

lim e 5b 1 =

0 1

5 b

Для краткости в будущем можно не использовать знак lim а просто

записывать так: e 0 подразумевая при этом, что промежуточным действием был вычислен данный предел.

Ответ. 15 .

Задача 2. Вычислить несобственный интеграл 1 рода xe x dx .

Решение. На этом примере мы ещѐ раз вспомним метод интегрирования по частям.

xe x dx =

lim

xe x dx . Интегрируем по частям.

Обозначим u x,

v e x . Тогда u 1,

v e x .

Тогда далее lim

lim e

			xe		x		b						x	b	= lim be				b	0 lim e	b	1 =
					x		b						x	b					b		b
	lim								lim e
b							0			b				0		b				b
b							0			b				0		b				b
0 0						0 1 = 1.
Ответ. 1.
																									dx
Задача 3. Вычислить несобственный интеграл 1 рода																									dx
																											.
																							x2			4	.
																					0
									dx			1			x		1	arctg( ) arctg(0) =
									dx			1			x		1
Решение.											=		arctg			=
Решение.								x	2	4	=	2	arctg		2	=	2
						0		x		4		2			2	0	2
	1					0										0
	1									Здесь символом arctg( ) фактически обозначается
				0		=			.
				0		=			.
	2	2						4
такой предел:									lim arctg(t) .
									t
Ответ.				.
				4
																										1
Задача 4.						Вычислить несобственный интеграл 1 рода																				1		dx .

																								x	2	4x 8
																						0		x		4x 8
																						0

Решение. Кстати, на этом примере мы ещѐ раз повторим алгоритм

							1							1
выделения полного квадрата.							1	dx		=				1					dx =

					x	2	4x 8					(x		2)	2	2		2
				0	x		4x 8				0	(x		2)		2
				0							0
1	x 2		1	arctg( ) arctg(1) =					1
1	x 2		1						1
	arctg	=											=				.
	arctg	=											=				.
2	2	0	2						2		2		4			8
		0

<<< < Предыдущая 1 2 3 4 56 / 156 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023625.95 Кб06899.pdf
#
13.02.202149.22 Кб2690.pdf
#
05.02.2023505.3 Кб06905.pdf
#
05.02.2023475.83 Кб06990.pdf
#
13.02.2021815.65 Кб06OMkzBKrZ3.pdf
#
05.02.20232.15 Mб07005.pdf
#
05.02.2023618.28 Кб07014.pdf
#
05.02.2023225.21 Кб07046.pdf
#
05.02.20231.01 Mб47067.pdf
#
05.02.2023266.87 Кб17089.pdf
#
05.02.2023288.25 Кб07090.pdf