Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

6044

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.2 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

ТЕМА: Интегрирование по частям № 3. Вычислить xe3x dx .

Решение. Пусть u x , так надо, чтобы понизилась степень на

следующем шаге. Составим таблицу:

u x

e3x

u 1

v e3x

Тогда xe3x dx =

xe3x

e3x dx =

xe3x

e3x

C .

№ 4. Вычислить x cos5xdx .

Решение.

u x

sin 5x

u 1

v cos5x

x cos5xdx =

x sin 5x

sin 5xdx

x sin 5x

cos5x C .

ТЕМА: Рациональные дроби.

№ 5. Вычислить интеграл	x2 x 3
		dx .
	(x 1)2 (x 2)

Решение. Как видим, здесь корень 1 имеет кратность 2. Разложение на простейшие дроби нельзя проводить так, как будто бы здесь три

независимых

множителя

(x 1) ,

(x 2) ,

т.е.

, иначе

получится

противоречие,

ведь

общий

x 1

знаменатель будет содержать всего лишь 1-ю степень (x 1) но никак не вторую. Надо степени знаменателя учитывать по возрастающей, до

кратности корня, а именно, так:	A	B	C		.

	x 1	(x 1)2	x	2

Приведём к общему знаменателю:

A(x 1)(x 2) B(x 2) C(x 1)2 . (x 1)2 (x 2)

Числитель этой дроби равен числителю исходной, той, которая была в интеграле:

A(x 2 x 2) B(x 2) C(x 2 2x 1) x 2 x 3 .

( A C)x 2 ( A B 2C)x ( 2 A 2B C) x 2 x 3 , система:

	A C 1
	A B 2C 1 . Построим расширенную матрицу и решим
	A B 2C 1 . Построим расширенную матрицу и решим

2 A 2B C 3

систему уравнений:

1	0	1	1	1	0

1	1	2 1		0	1
2	2	1		0	2
2	2	1	3	0	2

Система приведена к виду:

Тогда B 53 , C 95 , A 94

1	1	1	0	1	1

3	0	0	1	3	0	.
3	5	0	3	0	5
3	5	0	3	0	5

A C 1B 3C 0

3B 5

. И теперь интеграл распадается на сумму

трёх интегралов:	4	1	dx	5	1		dx	5	1	dx .
	9	x 1		3	(x 1)	2		9	x 2

В 1 и 3 слагаемых - как раньше, а вот во 2-м логарифм в ответе не получится, ведь тут уже 2-я а не 1-я степень в знаменателе.

	1	1
Полезно вспомнить, что			.
		x2
x

То есть, интеграл от -2 степени будет содержать -1 степень, и меняется знак.

Ответ:	4	ln	x 1	5 1	5	ln	x 2	C .


	9			3 x 1	9

ТЕМА: Иррациональности.

№ 6. Вычислить интеграл	x		x	1	dx .
№ 6. Вычислить интеграл					dx .
	3	x 1

Решение. Здесь есть корни порядка 2 и 3. Наименьшее общее кратное, НОК(2,3) = 6. Поэтому замена t 6 x 1 . При этом,

x 1 t 6 ,

x t 6 1 , dx 6t 5 dt ,

x 1 13 x 1 26 6

2 t 2 ,

x 1

x 1 12 x 1 36 6

3 t 3 .

x 1

t 6

1 t 3

Тогда

x x 1

6t 5 dt = 6 (t 6 1 t 3 )t 3dt =

t 2

x 1

6 (t 9 t 3 t 6 )dt

t10

t 4

t 7 C .

Сделаем обратную замену и получим ответ:

7 C .

x 1

ТЕМА: Тригонометрические функции. № 7. Вычислить интеграл sin3 x cos8 xdx .

Решение. Здесь нечётная степень синуса, применяем замену t cosx .

Тогда sin3 x cos8 xdx = 1 t 2

= 1

t 8

t 2 t 8 dt =

1 t 2

(1 t 2 )t8dt = (t10 t8 )dt =

t11

t 9

cos11 x

cos9 x

C .

№ 8. Вычислить интеграл

dx .

sin 3 x cos5 x

Решение. Здесь тоже суммарная степень чётная, замена t tgx .

dt . sin x

, cos x

t 2 1

1 t 2

																																										8
				1						dx =											1										1			dt =					1 t 2			8			1	dt =
	sin		3				5		x	dx =						t	3								1				t	2				dt =						t	3		t	2		dt =
	sin			x cos					x							t									1				t			1								t			t		1
																				3							5
															1 t 2					3			1 t 2				5
	t 2		1 4					1			dt =				t 2 1 3							dt =						t 6		3t 4 3t 2 1										dt
																																			3
		t		3		t	2		1								t	3																t	3
		t				t			1								t																	t
здесь мы воспользовались формулой (a b)3 a3																																						3a 2b 3ab2								b3 .
		3	3t		3				1			1				1			4			3			2	3ln							1 1				C .
		3							1			1				1			4			3			2								1 1
	t													dt	=			t						t							t
	t												3	dt	=			t						t							t					2
									t			t	3			4						2												2 t		2
									t			t				4						2												2 t

После обратной замены получаем ответ:

14 tg 4 x 32 tg 2 x 3ln tgx 12 ctg 2 x C .

445 ПРАКТИКА № 5 21.03.2016

1 xdx

Задача 1. Вычислить интеграл 0 (x 2 1)2 .

				1			xdx					1	1		2xdx						1	1
Решение.											=								=
Решение.					(x	2		1)	2		=	2		(x		2	1)	2	=		2
				0	(x			1)				2	0	(x			1)				2	0
				0									0									0
	1		1				1					1		1					1
										=						1 =				.
	2	12	1		02			1				2		2					4

3 xdx

Задача 2. Вычислить интеграл 0 1 x .

d (x2 1)		=	1 1		1	=


(x2	1)2
			2 x 2	1	0


Решение. При замене												x t , если x [0,3] то t [0, 3] .

3					3		t					3		t 2				3	(t 2 1) 1
3		xdx			3		t					3		t 2				3	(t 2 1) 1
			=						2tdt		= 2						dt	= 2						dt =
	1	x	=			1 t		2	2tdt		= 2		t	2			dt	= 2		t	2	1		dt =
0	1	x			0	1 t						0	t		1			0		t		1
0					0							0						0

	3				1															2
	3										3					3
2											3					3
		1					dt	= 2t				2arctgt						= 2 3					.
		1		2	1		dt	= 2t		0		2arctgt				0		= 2 3					.
			t	2						0						0					3
	0		t																		3

3		x 2
Задача 3. Вычислить интеграл		x 2	dx .


	x 2 1
2	x 2 1

Решение. Сделаем замену x 2 t , тогда t [0,1] .

3						1							1		2				1		2	1)	1
3		x 2				1	t						1	t	2				1	(t	2
		x 2		dx =			t		2tdt		=		2	t			dt =		2	(t				dt =
				dx =					2tdt		=		2				dt =		2					dt =
2	x 2 1					0	t 1						0	t		1			0			t 1
2						0							0						0
1			1					2	1			1						1
			1					2	1			1						1
2 t 1					dt	= t				2t		0	2ln(t 1)					0	= 2ln 2 1.
2 t 1					dt	= t				2t		0	2ln(t 1)					0	= 2ln 2 1.
0			t 1						0
									0

													2
Задача 4. Вычислить интеграл													xe x dx .
													0

Решение. Применим метод интегрирования по частям,

u x ,

xe x dx

Задача

v e x ,		тогда u 1,	v e x .
	2	2		2 = 2e2 (e2 e0 ) = e2 1 .
= xe x		e x dx = 2e2 e x
	0	0		0

5. Вычислить интеграл x cos xdx .

Решение. Тоже решается интегрированием по частям,

u x ,	v cosx ,	тогда u 1,			v sin x .
			0			0 =
x cos xdx = x sin x				sin xdx = sin 0 cosx


0				0

0 0 cos cos0 = 1 1 2 .

Из строения графика видно, что ответ и должен был получиться отрицательным: изначально cos x имеет две одинаковые части площади над и под осью, и его интеграл был бы 0, а если мы умножаем на x , то сильнее увеличится по модулю именно та часть, которая дальше от 0, то есть отрицательная. Вот графики, зелёным показан cos x , красным x cos x .

								2	1		1
Задача 6.	Вычислить интеграл e									x	1	dx .
Задача 6.	Вычислить интеграл e									x	2	dx .
								1			x
								1
	2 1	1			2	1	1					2	1	1


Решение.	e x				dx = e x			2	dx = e x d
Решение.	e x		x	2	dx = e x			2	dx = e x d
	1		x		1		x					1		x
	1				1							1

используя известное выражение et dt et C , получим:

	1	2		1

e x			= e 2		e1	= e e .

		1

Повторение к контрольной. Контрольная работа (4 задачи).

45 минут: контрольная работа.

1.Подведение под знак дифференциала, преобразования.

2.Интегрирование по частям.

3.Интегрирование рациональных дробей.

4.Интегрирование иррациональностей и тригонометрических функций.

445 ПРАКТИКА № 6 01.04.2016 Задача 1.

Найти площадь фигуры, ограниченной линиями:

y	x 2	и y		1	.
			2
1	2			x 2 1

Решение. Рассмотрим чертёж, найдём точки пересечения графиков и увидим, какую часть плоскости они ограничивают. График

y					1				имеет макстмум в точке 0 и проходит выше, чем																														y				x 2		,
	2			x 2 1																																				1	2
				x 2 1																																					2
																																					1				1,			1
у которой, напротив, там минимум. Точки перечечения 1,																																							,
у которой, напротив, там минимум. Точки перечечения 1,																																							,
																																					2							2
		1					1					x2						1				x3			1											1						1
		1

S														dx	= arctgx												=																=
S														dx	= arctgx												=																=
						2													1
				x				1 2													6							4					4		6							6
		1																							1
			1	. Замечание. Мы могли воспользоваться тем фактом, что обе
2		3		. Замечание. Мы могли воспользоваться тем фактом, что обе
2		3
функции чётные, и фигура симметрична, вычислить площадь правой
																1		1					x2								1		1			x2

половины и удвоить: S																	2		1					2		dx			=	2			2	1		2		dx			=
																1 x			1					2							0 x			1		2
					1						x3		1							1										1


2arctgx					0				2					= 2		0		2				0				=						. Так даже легче,
2arctgx									2					= 2		0		2				0				=						. Так даже легче,
										6			0		4					6								2		3
										6					4					6								2		3

потому что на нижнем пределе подставлять 0, из-за этого меньше вычислений.

Задача 2. Найти площадь области, ограниченной линиями

y x 2 , y x, x 1

Здесь чертёж не представляет особых сложностей, парабола проходит выше, а линейная функция ниже, поэтому:

1				1			3	1			2
1				1			3	1			2
	x 2 (x) dx = x 2 x dx =					x				x
	x 2 (x) dx = x 2 x dx =
0				0		3		0	2
0				0				0
1		1	=	5	.
3		2	=	6	.
3		2		6

Ответ: 56 .

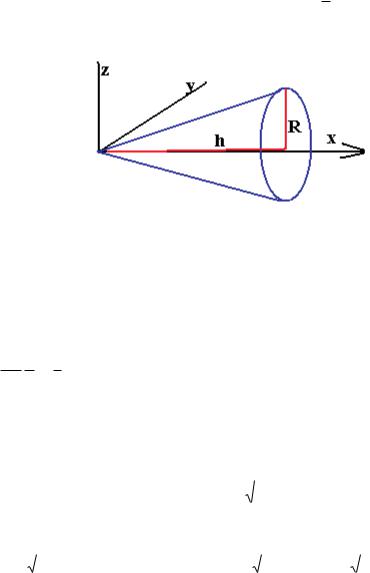
Задача 3. С помощью основной формулы вычисления объёмов тел вращения, доказать формулу объёма конуса V 13 R 2 h .

Решение. Для удобства применения основной формулы, повернём конус на 90 градусов, так, чтобы высота лежала на оси 0x .

На чертеже видно, что два катета имеют длины R и h . Тогда отрезок, вращением которого образована боковая поверхность конуса,

находится на прямой y f (x)

x .

(x)dx =

x dx

R 2 h = 1 R 2 h . 1 3 3

Задача 4. Найти длину 1 витка винтовой линии в пространстве

x R cost, y R sin t, z at t (0,2 )

Решение. В данном случае кривая параметрически задана, в 3-

		b
мерном пространстве. Формула L			(x (t))2 ( y (t))2 (z (t))2 dt .
		a
Производные: x R sin t, y R cost, z a .
2		2				2
L	R2 sin 2 t R2 cos2 t a 2 dt	=		R 2 a 2 dt =	R 2 a 2	1dt
0		0				0

Ответ: 2 R2 a2 .

Замечание. Если была бы не винтовая линия, а окружность, а это было бы при параметре a 0 , то как раз бы и получалось

2 R2 0 2 R длина окружности.

Несобственный интеграл.

Задача 5. Найти несобственный интеграл

					1						1
Решение.					1	dx =					1

			x	2	4x 8				(x 2)			2		2	2
	0		x		4x 8			0	(x 2)					2
	0							0
1	arctg( )	arctg(1)					1
						=					=			.
						=					=			.
2							2	2		4			8

			1
			1		dx .

	x2	4x 8
0
			1		x 2
			1		x 2
dx =				arctg		=
dx =				arctg		=
			2		2	0
					2	0

Здесь под символом arctg( ) понимается предел lim arctg(t) .

Задача 6. Выяснить сходимость по признакам сравнения:

sin x

dx .

x3 1

Решение. Так как

sin x 1, то заменив функцию

sin x

на

x3 1

sin x

получим

dx причём, по признаку сравнения в

x3 1

не предельной форме, если второй интеграл сходится (обозначим его (II)), то и исходный тоже сходится. А теперь заменим на ещё более простую функцию, но уже по признаку сравнения в предельной форме.

Бесконечно малая величина	1	при x эквивалентна	1	.


	x3 1		x3

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.02.2021280.15 Кб16036.pdf
#
05.02.2023540.2 Кб06038.pdf
#
05.02.2023617.72 Кб16040.pdf
#
05.02.2023540.44 Кб06041.pdf
#
05.02.2023305.26 Кб06042.pdf
#
05.02.20231.2 Mб16044.pdf
#
13.02.2021517.85 Кб06045.pdf
#
13.02.2021177.86 Кб06060.pdf
#
13.02.2021938.68 Кб26077.PDF
#
13.02.2021344.02 Кб06079.pdf
#
05.02.2023757.12 Кб266082.pdf