Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

6691

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

594.07 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

2 семестр

Контрольная работа № 1.

1.Подведение под знак дифференциала, преобразования.

2.Интегрирование по частям.

3.Интегрирование рациональных дробей.

4.Интегрирование иррациональностей и тригонометрических функций.

Варианты для самостоятельного решения:

Вариант 1. Найти неопределѐнные интегралы:

x 5

2x2 10x 13

dx 2. x sin 2xdx

1 x

(x 2)(x

Вариант 2. Найти неопределѐнные интегралы:

4x 6

dx 2). x cos3xdx

2x2 2x 1

cos5 x

(x 4)(x 1)

sin

Аналогичные задачи из практических занятий:

Задача 1.1. Вычислить x cos(x2 )dx .

Решение. x cos(x2 )dx

cos(x2 )(2xdx)

cos(x2 )d (x2 ) =

costdt =

sin t C

sin(x2 ) C .

Ответ.

sin(x2 ) C .

Задача 1.2. Вычислить

dx .

4x 20

Решение. Дискриминант знаменателя отрицательный, поэтому здесь невозможно сделать как в прошлой задаче, так как нет корней

знаменателя и дробь невозможно свести к виду																												1		.

																											(x a)( x b)
Но при D < 0 можно выделить полный квадрат:
				1						dx				=					1				dx =	1					dx .

	x		2	4x					20							(x 2)				2				(x 2)	2	4		2
	x			4x					20							(x 2)					16			(x 2)		4
С помощью замены t x 2 сводится к интегралу:
				1						1							t		C
							dt		=				arctg									, и далее с помощью обратной замены
		2		4	2		dt		=				arctg									, и далее с помощью обратной замены
	t			4						4								4
												1						x 2
получаем ответ:															arctg							C .
получаем ответ:															arctg							C .
												4							4
						1					x 2							C .
Ответ.								arctg
Ответ.								arctg
						4									4

Задача 2.1. Вычислить xe3x dx .

Решение. Пусть u x , так надо, чтобы понизилась степень на следующем шаге. Составим таблицу:

u x	v		1		e3x
			1
			3
			3
u 1	v e3x
Тогда xe3x dx =							1		xe3x	1	e3x dx =	1	xe3x	1	e3x C .
Тогда xe3x dx =									xe3x		e3x dx =		xe3x		e3x C .
			3							3		3		9
Ответ.	1	xe3x				1		e3x C .
Ответ.		xe3x						e3x C .
	3		9
Задача 2.2. Вычислить x cos5xdx .
Решение.
u x	v		1	sin 5x
			1
			5
			5
u 1	v cos5x

x cos5xdx =

x sin 5x

sin 5xdx =

x sin 5x

cos5x C .

Ответ.

x sin 5x

cos5x C .

Задача 3. Вычислить интеграл

x2 x 3

dx .

(x 1)2 (x 2)

Решение. Как видим, здесь корень 1 имеет кратность 2. Разложение на простейшие дроби нельзя проводить так, как будто бы здесь три

независимых

множителя

(x 1) ,

(x 2) ,

т.е.

, иначе

получится

противоречие,

ведь

общий

x 1

знаменатель будет содержать всего лишь 1-ю степень (x 1) но никак не вторую. Надо степени знаменателя учитывать по возрастающей, до

кратности корня, а именно, так:	A	B	C		.

	x 1	(x 1)2	x	2

Приведѐм к общему знаменателю:

A(x 1)(x 2) B(x 2) C(x 1)2 . (x 1)2 (x 2)

Числитель этой дроби равен числителю исходной, той, которая была в интеграле:

A(x 2 x 2) B(x 2) C(x 2 2x 1) x 2 x 3 .

( A C)x 2			( A B 2C)x ( 2 A 2B C) x 2					x 3 , система:
		A C 1
	A B 2C 1 .			Построим расширенную матрицу и решим
	A B 2C 1 .			Построим расширенную матрицу и решим

2 A 2B C 3
систему уравнений:
	1	0	1 1		1 0	1 1	1 0	1 1

	1	1	2 1		0 1	3 0	0 1	3 0	.
		2			0 2	3 5	0 3	0 5
2		2	1 3		0 2	3 5	0 3	0 5

Система приведена к виду:

Тогда B 53 , C 95 , A 94

A C 1B 3C 0

3B 5

. И теперь интеграл распадается на сумму

трѐх интегралов:	4	1	dx	5	1		dx	5	1	dx .
	9	x 1		3	(x 1)	2		9	x 2

В 1 и 3 слагаемых - как раньше, а вот во 2-м логарифм в ответе не получится, ведь тут уже 2-я а не 1-я степень в знаменателе.

	1	1
Полезно вспомнить, что			.
		x2
x

То есть, интеграл от -2 степени будет содержать -1 степень, и меняется знак.

Ответ.

x 1

5 1

x 2

C .

3 x 1

Задача 4.1. Вычислить интеграл

dx .

x 1

Решение. Здесь есть корни порядка 2 и 3. Наименьшее общее кратное,

НОК(2,3) = 6. Поэтому замена

t 6 x 1 . При этом,

x 1 t 6 , x t 6 1 , dx 6t 5 dt ,

x 1 13 x 1 26 6

2 t 2 ,

x 1

x 1 12 x 1 36 6

3 t 3 .

x 1

t 6

1 t 3

x x 1

Тогда

6t 5 dt = 6 (t 6 1 t 3 )t 3dt =

t 2

3 x 1

6 (t 9 t 3 t 6 )dt

t10

t 4

t 7 C .

Сделаем обратную замену и получим ответ:

7 C .

Ответ.

x 1

Задача 4.2. Вычислить интеграл																																										1								dx .

																																				sin 3 x cos5 x
Решение. Здесь тоже суммарная степень чѐтная, замена t tgx .
dx							1				dt . sin x												t					,		cos x												1					.

				t 2			1
				t 2			1														1 t 2																				1 t 2
																																																								8
							1								dx =													1														1			dt					=			1 t 2			8			1	dt =
	sin		3									5		x	dx =								t	3									1							t	2				dt					=				t	3		t	2		dt =
	sin					x cos								x									t										1							t			1											t			t		1
																											3											5
																						1 t 2					3				1 t 2							5
	t 2		1 4										1			dt =					t 2 1 3									dt =									t 6		3t 4 3t 2 1													dt
		t			3					t		2				dt =								t	3					dt =															t	3								dt
		t								t				1										t																					t
здесь мы воспользовались формулой (a b)3																																																a3				3a 2b 3ab2								b3 .
		3	3t 3											1			1						1			4				3			2		3ln									1 1							C .
		3												1			1						1			4				3			2											1 1
	t																			dt	=				t							t										t
	t																	3		dt	=				t							t										t							2
														t			t	3					4							2															2 t				2
														t			t						4							2															2 t
После обратной замены получаем ответ:
Ответ.								1	tg				4 x					3	tg 2 x 3ln										tgx					1			ctg 2 x C .
								1										3																1

							4											2															2
							4											2															2

Контрольная работа № 2.

1.Определѐнный интеграл и его приложения.

2.Несобственный интеграл.

3.Двойной интеграл.

4.Дифф. уравнения 1 порядка с разделяющимися переменными.

Варианты для самостоятельного решения: Вариант 1.

1.Вычислить площадь области, ограниченной кривыми: y x3 , y x , x 1.

cosx dx 1 sin 2 x

2.Найти несобственный интеграл 1 x 2 1 dx .

3.Найти двойной интеграл (x y)dxdy , где D - треугольник с

вершинами (0,0), (1,1), (1,3).

4. Решить дифф. уравнение y 4x3 y .

Вариант 2.

1.Вычислить площадь области, ограниченной кривыми: y x 2 , y 2x , x 1.

2. Найти несобственный интеграл e 6 x dx .

3.Вычислить в полярных координатах интеграл от функции f x3 y по 1-й четверти круга радиуса 1.

4.Дифф. уравнение 1 порядка y 3x 2 y .

Аналогичные задачи из практических занятий:

Задача 1.1. Вычислить

					0
2		cosx			2	d (sin x)
Решение.					dx =
Решение.	1	sin	2	x	dx =	1 sin	2	x
0	1	sin		x	0	1 sin		x
0					0

здесь мы можем заменить sin x на t , но тогда нужно сделать пересчѐт верхнего и нижнего пределов. Если x [0, 2] то t [sin(0), sin( 2)] ,

т.е. t [0,1] .

1		dt			10						.
				= arctg(t)		= arctg(1) arctg(0)	=		0	=

		t	2					4
	1		2								4
0	1										4
0

А можно было сначала вычислять интеграл как неопределѐнный, тогда надо было бы вернуться к исходной переменной x (то есть сделать обратную замену), но пределы можно не пересчитывать.

d (sin x)

= arctg(t) C = arctg(sin x) C

1 sin

1 t

arctg(sin x)

= arctg sin

arctg sin 0 = arctg(1)

arctg(0) = .

Ответ.

Задача 1.2. Найти площадь области, ограниченной линиями

y x 2 , y x, x 1

Решение.

1	1		3	1			2	1
1	1		3	1			2	1
x 2 (x) dx = x 2 x dx =		x				x
x 2 (x) dx = x 2 x dx =
0	0	3		0	2			0
0	0			0				0

Ответ. 56 .

Задача 2. Найти несобственный интеграл

			1		1
Решение.			1	dx =	1

	x	2	4x 8		(x 2)	2	2	2
0	x		4x 8	0	(x 2)		2
0				0

= 13 12 = 56 .

			1
			1		dx .

	x2	4x 8
0
			1		x 2
			1		x 2
dx =				arctg		=
dx =				arctg		=
			2		2	0
					2	0

1	arctg( ) arctg(1) =	1
					=		.
					=		.
2		2	2	4		8

Здесь под символом arctg( ) понимается предел lim arctg(t) .

Ответ. 8 .

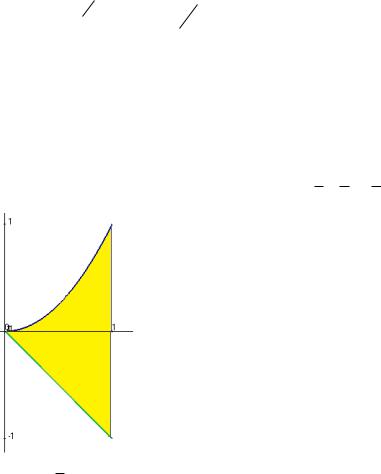
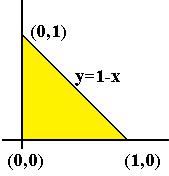
Задача 3.1. Вычислить интеграл (x y)dxdy по треугольнику D,

вершины которого: (0,0),(1,0),(0,1).

Решение. Строение треугольника понятно (см. чертѐж). Наклонная линия задаѐтся уравнением y 1 x .

1	1 x	1		y	2	1 x
1	1 x	1			2	1 x
Вычисление: dx (x y)dy			1 x
			1 x
		= xy	0
		= xy	0	2
0	0	0		2		0
		0				0

dx =

	1						(1 x)			2					1	2			1 2x x 2		1	1	x 2

x(1 x)								2			dx			=	x x				2	dx =		2		dx	=
	0							2							0				2		0	2	2
	x	1		x3	1	=	1		1			1	.		Ответ.		1	.



2		0	6		0		2	6				3					3
2		0	6				2	6				3					3
															x9 ydxdy , где D - четверть круга радиуса 1
Задача 3.2. Вычислить															x9 ydxdy , где D - четверть круга радиуса 1

(в первой координатной четверти).

Решение. Заменим x cos ,	y sin , а также умножим на
якобиан .

2 1												2	1
				9											11	9
( cos)					( sin ) d					d		=				cos	sin d d =
0 0												0		0
2							12	1		1		2
2							12	1				2
		9										9
	cos		sin						d =		cos		sin d
	cos		sin			12			d =	12	cos		sin d
0						12		0		12	0
0								0			0

Дальше остаѐтся интеграл от одной переменной, там можно применять обычный способ, подведение под знак дифференциала.

1		2										1			2
1		cos9 sin d =										1			cos9 ( sin d ) =
		cos9 sin d =													cos9 ( sin d ) =
12	0							12							0
	0														0

	1		2												1	1					2			1					1
	1		cos9 d (cos ) =												1	1		cos10			2	=		1		(0 1) =			1	.
12			0											12 10							0		120					120
			0		1		.														0
Ответ.					1
Ответ.				120
				120
Задача 4.						Решить уравнение											y xy .
Решение.						y xy					dy		xy						dy	xdx					dy		xdx
											dx								y							y
ln	y			x 2		C			y	eC1 e x2						2		y Ce x2 2 .
				x 2

				2		1
				2				x2
					y Ce			x2
Ответ.					y Ce			2 .

Проверка. Если y Ce x2 2 , то y Cxe x2 2 , действительно, производная имеет лишний множитель x по сравнению с исходной функцией, и подходит в качестве решения уравнения y xy .

Контрольная работа № 3.

1.Линейные дифф. уравнения 2 порядка с задачей Коши.

2.Действия с комплексными числами.

3.Формула Муавра.

4.Числовые ряды.

Вариант для самостоятельного решения:

1. Решить линейное однородное уравнение y 5y 4y 0 , найти частное решение при y(0) 2 , y (0) 3 .

2. Поделить 1 5i .

1 7i

3. Вычислить в показательной форме: (3 i)9 ответ дать в виде a+bi.

( 1) n 2n

4. Исследовать сходимость ряда

n 1 n!

Аналогичные задачи из практических занятий:

Задача 1. Найти частное решение дифф. уравнения y 10y 9 y 0 при условиях Коши: y(0) 1, y (0) 7 .

Решение. Характеристическое уравнение: r 2 10r 9 0 , его корни: r1 1, r2 9 . Тогда ФСР состоит из e x и e9 x , общее решение такое:

y C1e x C2 e9 x .

Теперь найдѐм решение задачи Коши. Сначала запишем функцию и еѐ производную:

y C e x C		e9 x и	y C e x 9C		e9 x .
1	2		1	2

Кроме того, у нас есть информация: y(0) 1, y (0) 7 .

Тогда C1 C2 1 , C1 9C2 7 . Получается система уравнений

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20231.66 Mб06654.pdf
#
13.02.2021987.09 Кб16655.pdf
#
05.02.2023246.51 Кб06666.pdf
#
05.02.2023246.56 Кб06667.pdf
#
05.02.2023233.02 Кб06679.pdf
#
05.02.2023594.07 Кб06691.pdf
#
13.02.2021163.64 Кб06693.pdf
#
05.02.2023534.33 Кб2670.pdf
#
05.02.20231.44 Mб06701.pdf
#
13.02.20211.28 Mб96704.pdf
#
05.02.2023645.59 Кб06705.pdf