Элементы электронной техники.-4

5.2.Примеры решения задач по определению физических свойств, описываемых тензорами четвертого ранга

При решении задач для правильного выбора кристаллофизической системы координат в заданном кристалле рекомендуется использовать Таблицу 2 (стереографические проекции точечных групп симметрии) и Таблицу 4 (формы матриц упругих постоянных кристаллов различных сингоний). Таблица 2 находится в первой части учебного методического пособия, а Таблица 4 – в конце данной части.

Задача 1. Определить величину и характер деформаций, испытываемых кристаллом низкотемпературного кварца при его одноосном сжатии в направлении оси Х1 с усилием 103 Н / м, если модули податливости кварца имеют следующие значения (в ед. СГСЕ):

S11 S22 128 10 14, S33 95.6 10 14 . Коэффициент перевода податливости из системы СГСЕ в системуединиц СИ таков: 1 ед. СГСЕ =1 см2/дин = 10 м2/Н.

Решение. Кварц в данной модификации имеет симметрию 32, причем в стандартной установке кристаллофизической системы координат ось Х1 параллельна

(символ « ») оси симметрии 2. Для вычисления возникающих деформаций кристалла необходимо воспользоваться законом Гука в форме:

ij Sijkl kl

Вданном случае тензор упругих напряжений задан следующим образом: 33 103 Н / м,

остальные компоненты тензора упругих напряжений равны нулю. Поэтому выражение (1) можно переписать:

ij Sij33 33

кварца из требуемых для решения значений Sm3 имеет отличные от нуля только три компоненты. Поэтому, изменяя значения индекса m от 1 до 3, из (2) получим тензор деформаций. Для других значений индекса компоненты тензора деформаций равны нулю,

т.к. равны нулю соответствующие модули податливости кварца. Но значения индекса m =

61

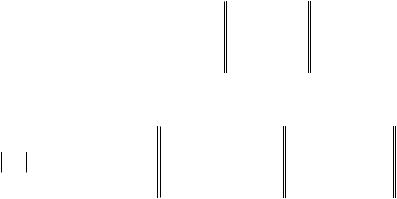
1, 2, 3 обозначают только диагональные элементы тензора деформаций (см. стр. 45

данного пособия), т.е. этот тензор деформации будет иметь диагональный вид:

1 0 0

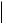m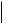 0 2 0 0 0 3

Значит, в окончательном виде будем иметь следующий тензор деформаций:

Из его вида следует, что при сжатии кристалла кварца вдоль оси симметрии третьего порядка кристалл испытывает одноосные деформации по всем трем направлениям: Х1, Х2, Х3, другими словами, кристалл изменяет свои размеры по всем трем измерениям.

Задача 2. Определить величину и характер упругих напряжений, испытываемых кристаллом низкотемпературного кварца при его деформации на величину 10 6 вдоль оси симметрии третьего порядка, если известно, что упругие постоянные кварца по осям равны следующим значениям (в ед. СГСЕ): C12 C22 10.4 1010, C33 107 1010 . Перевод из СГСЕ в систему СИ производится с коэффициентом 1 ед. СГСЕ = 10-1 Н/м2.

Решение. Данная задача является обратной по отношению к предыдущей. Поэтому для её решения воспользуемся законом Гука в виде:

ij Cijkl kl .

Поскольку тензор упругой деформаций задан по условию задачи, а вид тензора упругих постоянных 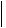Cijkl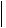 известен из справочных данных (см. Таблицу 4 Приложения),

то нетрудно найти вид тензора упругих напряжений. В обозначениях Фохта он будет выглядеть так:

m Cmn n Cm3 3.

Перебирая значения индекса m от 1 до 3, получим все отличные от нуля компоненты:

62

Таким образом, деформация кристалла вдоль оси симметрии третьего порядка привела к возникновению одноосных упругих напряжений по трем взаимно перпендикулярным направлениям: Х1, Х2, Х3.

Задача 3. Определить упругость кристалла низкотемпературного кварца в

направлении единичного вектора n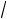(1 2, 1 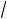2, 0) , если упругие постоянные кварца

равны следующим значениям (в ед. СГСЕ): C11 86 1010, C12 4.8 1010, C13 10.4 1010,

C14 18.2 1010 , C33 107.1 1010, C44 58.6 1010, C66 40.5 1010 .

Решение. Величина физического свойства четвертого ранга в направлении

единичного вектора n вычисляется как нормальная составляющая тензора (см. Учебное пособие по курсу.)

Cn Cijkl ni n j nk nl ,

представляющее собой сумму по всем четырем индексам. Поскольку по условию задачи n3 = 0, то индексы i, j, k, l могут принимать только значения 1 и 2. Следовательно в обозначениях Фохта будем иметь (см. Таблицу 4):

12 2C11 4C12 4C66 C11 2C12 2C66.

Подставив численные значения упругих постоянных, найдем (в ед. СГСЕ)

Cn 86 2 4.8 2 40.5 1010 176.6 1010 1.8 1012 .

Переведем результат в систему СИ: Cn 1.8 1012 10 1 1.8 1011 Н / м2 .

63

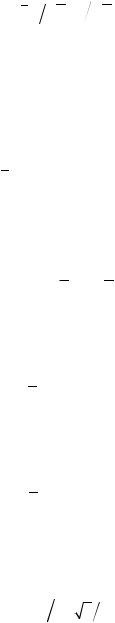
Такое значение упругой постоянной кристалла низкотемпературного кварца следует

ожидать в направлении n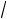(1 2, 1 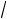2, 0) .

5.3.Варианты заданий по определению физических свойств, описываемых тензорами четвертого ранга

1. Определить упругость кристалла низкотемпературного кварца в направлении

единичного вектора n(1 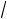2, 0, 1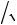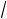2) . Форму матрицы упругих постоянных Cijkl Cmn

взять из Таблицы 4, а значения упругих постоянных - из задачи 2.

2. Определить упругость кристалла низкотемпературного кварца в направлении

единичного вектора n(0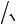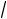, 12, 1 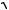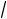2) . Форму матрицы упругих постоянных Cijkl Cmn

взять из Таблицы 4, а значения упругих постоянных - из задачи 2.

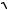
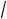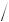3. Определить упругость кристалла низкотемпературного кварца в направлении единичного вектора n(32, 1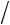2, 0) . Форму матрицы упругих постоянных Cijkl Cmn

взять из Таблицы 4, а значения упругих постоянных - из задачи 2.

4. Определить упругость кристалла низкотемпературного кварца в направлении единичного вектора n(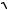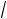3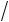2, 0, 12) . Форму матрицы упругих постоянных Cijkl Cmn

взять из Таблицы 4, а значения упругих постоянных - из задачи 2.

5. Определить упругость кристалла низкотемпературного кварца в направлении

6. Определить величину и характер деформаций, испытываемых кристаллом низкотемпературного кварца при его одноосном сжатии в направлении оси Х2 с усилием 103 Н / м2, если модули податливости кварца имеют следующие значения (в ед. СГСЕ):

податливостей взять из Таблицы 4 Приложения. Коэффициент перевода модулей податливости из системы СГСЕ в систему единиц СИ: 1 ед. СГСЕ = 1 см2/дин = 10 м2/Н.

64

7. Определить величину и характер деформаций, испытываемых кристаллом низкотемпературного кварца при его одноосном сжатии в направлении оси Х3 с усилием 103 Н / м2, если его модули податливости имеют следующие значения (в ед. СГСЕ):

S13 S23 11.0 10 14, S33 95.6 10 14 . Форму матрицы упругих постоянных взять из Таблицы 4. Коэффициент перевода модулей податливости из системы СГСЕ в систему единиц СИ таков: 1 ед. СГСЕ =1 см2/дин = 10 м2/Н.

8. Определить величину и характер деформаций, испытываемых кристаллом резорцина (точечная группа симметрии mm2, форма матрицы упругих постоянных приведена в Таблице 4) при его одноосном сжатии в направлении оси Х1 с усилием 103 Н / м2, если модули податливости резорцина имеют следующие значения (в ед. СГСЕ):

S11 19 10 12, S22 11 10 12, S33 15 10 12, S44 31 10 12,

S55 23 10 12, S66 25 10 12, S12 4 10 12, S13 3 10 12, S23 9 10 12.

Коэффициент перевода модулей податливости из системы СГСЕ в систему единиц СИ таков: 1 ед. СГСЕ =1 см2/дин = 10 м2/Н.

9. Определить величину и характер деформаций, испытываемых кристаллом резорцина (точечная группа симметрии mm2, форма матрицы упругих постоянных приведена в Таблице 4) при его одноосном сжатии в направлении оси Х2 с усилием 103 Н / м2, если модули податливости резорцина имеют следующие значения (в ед. СГСЕ):

S11 19 10 12, S22 11 10 12, S33 15 10 12, S44 31 10 12,

S55 23 10 12, S66 25 10 12, S12 4 10 12, S13 3 10 12, S23 9 10 12.

10. Определить величину и характер деформаций, испытываемых кристаллом резорцина (точечная группа симметрии mm2, форму матрицы упругих податливостей взять из Таблицы 4) при его одноосном сжатии в направлении оси Х3 с усилием 103 Н / м2, если модули податливости резорцина имеют следующие значения (в ед. СГСЕ):

S11 19 10 12, S22 11 10 12, S33 15 10 12, S44 31 10 12,

S55 23 10 12, S66 25 10 12, S12 4 10 12, S13 3 10 12, S23 9 10 12.

11. Определить величину и характер упругих напряжений, испытываемых кристаллом резорцина (точечная группа симметрии mm2, форма матрицы упругих постоянных приведена в Таблице 4 Приложения) при его деформации на величину 10 6

65

вдоль оси Х1, если известно, что его упругие постоянные таковы (в ед. СГСЕ):

C11 10 1010, C22 14 1010, C33 13 1010, C44 3 1010, C55 4 1010,

C66 4 1010, C12 6 1010, C13 7 1010, C23 7 1010.

Перевод из СГСЕ в систему СИ осуществляется с коэффициентом 1 ед. СГСЕ = 10-1

Н/м2.

12. Определить величину и характер упругих напряжений, испытываемых кристаллом резорцина (точечная группа симметрии mm2, форма матрицы упругих постоянных приведена в Таблице 4 Приложения) при его деформации на величину 10 5 вдоль оси Х2, если его упругие постоянные принимают следующие численные значения (в ед. СГСЕ):

C11 10 1010, C22 14 1010, C33 13 1010, C44 3 1010, C55 4 1010,

C66 4 1010, C12 6 1010, C13 7 1010, C23 7 1010.

13. Определить величину и характер упругих напряжений, испытываемых кристаллом резорцина (точечная группа симметрии mm2, форма матрицы упругих постоянных приведена в Таблице 4) при его деформации на величину 10 7 вдоль оси Х3 , если его упругие постоянные имеют следующие численные значения (в ед. СГСЕ):

C11 10 1010, C22 14 1010, C33 13 1010, C44 3 1010, C55 4 1010,

C66 4 1010, C12 6 1010, C13 7 1010, C23 7 1010.

14. Определить величину и характер упругих напряжений, испытываемых кристаллом ниобата лития (точечная группа симметрии 3m, форма матрицы упругих постоянных приведена в Таблице 4) при его деформации на величину 10 6 вдоль оси Х1 , если его упругие постоянные принимают следующие численные значения (в ед. СГСЕ):

C11 20 1010, C22 C11, C33 24 1010, C44 6 1010, C55 C44,

C66 4 1010, C12 5 1010, C13 7.5 1010, C23 0.9 1010.

15. Определить величину и характер упругих напряжений, испытываемых кристаллом ниобата лития (точечная группа симметрии 3m, форма матрицы упругих постоянных приведена в Таблице 4) при его деформации на величину 3 10 6 вдоль оси Х2, если его упругие постоянные принимают следующие численные значения (в ед. СГСЕ):

C11 20 1010, C22 C11, C33 24 1010, C44 6 1010, C55 C44,

66

C66 4 1010, C12 5 1010, C13 7.5 1010, C23 0.9 1010.

16. Определить величину и характер упругих напряжений, испытываемых кристаллом ниобата лития (точечная группа симметрии 3m, форму матрицы упругих постоянных взять из Таблицы 4) при его деформации на величину 5 10 5 вдоль оси Х , если его упругие постоянные принимают следующие численные значения (в ед. СГСЕ):

C11 20 1010, C22 C11, C33 24 1010, C44 6 1010, C55 C44,

C66 4 1010, C12 5 1010, C13 7.5 1010, C23 0.9 1010.

17. Определить величину и характер упругих напряжений, испытываемых кристаллом германия (точечная группа симметрии m3m, форму матрицы упругих постоянных взять из Таблицы 4 Приложения) при его деформации на величину 10 4 вдоль оси Х3 , если его упругие постоянные принимают следующие численные значения (в

ед. СГСЕ): C11 131 1010, C22 C11, C33 C11, C44 68 1010, C12 49 1010.

18. Определить величину и характер упругих напряжений, испытываемых кристаллом хлористого калия (точечная группа симметрии m3m, форму матрицы упругих постоянных взять из Таблицы 4 Приложения) при его деформации на величину 8 10 3 вдоль оси Х3 , если его упругие постоянные имеют следующие численные значения (в ед.

кристаллом кремния (точечная группа симметрии m3m, форму матрицы упругих постоянных взять из Таблицы 4) при его деформации на величину 4 10 7 вдоль оси Х3, если его упругие постоянные принимают следующие численные значения (в ед. СГСЕ):

C11 166 1010, C22 C11, C33 C11, C44 80 1010, C12 64 1010.

20. Определить величину и характер упругих напряжений, испытываемых кристаллом арсенида галлия (точечная группа симметрии m3m, форму матрицы упругих постоянных взять из Таблицы 4) при его деформации на величину 7 10 6 вдоль оси Х3., если его упругие постоянные принимают следующие численные значения (в ед. СГСЕ):

C11 1.2 1010, C22 C11, C33 C11, C44 0.54 1010, C12 0.59 1010.

67

6. ЛИТЕРАТУРА

1.Ю.И. Сиротин, М.П. Шаскольская. Основы кристаллофизики. М.: Наука, 1979. – 639 с.

2.Н.В. Переломова, М.М. Тагиева. Задачник по кристаллофизике. М.: Наука, 1972. – 142 с.

3.Б.А. Струков. Сегнетоэлектричество. М.: Наука, 1979.

4.И. Костов. Кристаллография. М.: Мир, 1965.

5.И.С. Желудев. Симметрия и её приложения. М.: Атомиздат, 1976.

6.В.Н. Давыдов В.Н. Материалы и элементы электронной техники. Часть 1. Фундаментальные свойства кристаллических материалов. Томск, ТМЦ ДО, 2003. – 231 с.

68

ПРИЛОЖЕНИЯ

69