
Физика конденсированного состояния.-2
.pdf
Показатель преломления определяется как отношение скорости света в вакууме
к скорости света в среде кристалла, а именно: |
|
n c /V . |
(5.11) |
Величина ķ характеризует поглощение света средой кристалла и называется по-
казателем поглощения, или коэффициентом экстинкции.
Величины k и α связаны между собой соотношением:
|
2 k |
|
c |
||
|
|
4 k |
|
c |
||
|
4 kn
.
(5.12)
Из общего курса физики известна связь диэлектрической проницаемости и по-
казателя преломления п:
n |
. |
Коэффициент отражения R можно выразить через n и ķ:
|
(n 1) |
2 |
k |
2 |
|
|
R |
|
|
. |
|||
(n 1) |
2 |
k |
2 |
|||
|
|
|||||
|
|
|
|
(5.13)
(5.14)
Формула (5.14) непосредственно связывает коэффициенты отражения R и по-
глощения α, если подставить в неё выражение ķ. из уравнения (5.12). Если поглоще-
ние весьма мало, то коэффициент отражения выражается классической зависимо-
стью:
R(n 1) (n 1)
2 2
.
(5.15)
При больших значениях показателя преломления (n>>1) происходит почти полное отражение R ≈ 1. Если наоборот, поглощение велико и ķ >> n, то также R ≈ 1
и происходит почти полное отражение. Именно этому второму случаю соответству-
ет обычно наблюдаемый зеркальный блеск металлов и многих полупроводников, так как коэффициент поглощения этих материалов в видимой области спектра очень высокий (α > 104 см-1).
Особенности спектральных зависимостей оптических коэффициентов R(λ), Т(λ)
и α(λ) в разных областях спектра объясняются различными механизмами взаимодей-
ствия световой волны со средой кристалла и главным образом различными меха-
низмами поглощения энергии световой волны кристаллом. Поэтому теория оптиче-
ских явлений развита применительно к анализу спектров поглощения света. Однако
31
при больших значениях коэффициента поглощения α, как это видно из формулы
(5.6), значение интенсивности прошедшего света очень мало и для того, чтобы определить его требуются измерения на очень тонких образцах (достаточно указать,
что для α ≈ 104 см-1 приходится использовать образцы с толщиной d = 10-4 см-1= 1 мкм). В этом случае растут экспериментальные погрешности как за счет ошибки измерения толщины образца, так и за счет увеличивающегося влияния качества обработки поверхности образца.
Основные механизмы поглощения света в полупроводниках
Пусть величина αi(ω) имеет смысл вероятности поглощения фотона с частотой
ω на единице толщины образца при действии некоторого i-того механизма погло-
щения и все механизмы поглощения действуют независимо друг от друга, тогда полная вероятность поглощения будет выражаться следующим образом:
( )
N i ( )
i 1
.
(5.16)
Таким образом, в данном спектральном интервале следует учитывать механиз-
мы поглощения, дающие наибольший вклад, т. е. имеющие наибольшее значение величины αi(ω). В различных спектральных интервалах можно выделить преобла-
дающие механизмы поглощения.
Поскольку поглощение света связано с переходом энергии фотонов в другие виды энергии в кристаллах, то естественно классифицировать механизмы поглоще-
ния следующим образом:
1)собственное или фундаментальное поглощение, связанное с электронными переходами между разрешенными зонами энергии;
2)поглощение свободными носителями заряда, связанное с электронными (или дырочными) переходами внутри соответствующих разрешенных зон или между подзонами разрешенных зон;
3)примесное поглощение, связанное с электронными (или дырочными) пере-
ходами между разрешенными зонами и примесными уровнями в запрещенной зоне; 4) межпримесное поглощение, связанное с электронными (или дырочными) пе-
32
реходами между примесными состояниями в запрещенной зоне;
5)экситонное поглощение, связанное с созданием или распадом экситонных состояний;
6)фононное поглощение, связанное с поглощением энергии световой волны колебаниями атомов решетки и рождением в решетке при этом новых фононов;
7)плазменное поглощение, связанное с поглощением энергии световой волны электронно-дырочной плазмой и приводящее к переходу плазмы в более высокие квантованные состояния.
Следует отметить, что почти все механизмы оптического поглощения, связан-
ные с различными электронными (или дырочными) переходами, сопровождаются поглощением или испусканием фононов. Необходимость участия фононов в процес-
сах поглощения света, связанных с электронными (или дырочными) переходами,
обусловлена требованием выполнения закона сохранения импульса. Это связано с тем, что большое изменение импульса электронов (или дырок) при некоторых пере-
ходах, не может быть вызвано обычно малыми импульсами поглощаемых в этих пе-
реходах фотонов и требует участия фононов, которые могут иметь достаточно большой импульс. Таким образом, в механизмах поглощения 1 – 5 мы часто имеем дело с комбинированным поглощением, в котором участвуют, как электроны и дыр-
ки, так и фононы.
Электронные переходы, соответствующие механизмам поглощения 1 – 5, изоб-
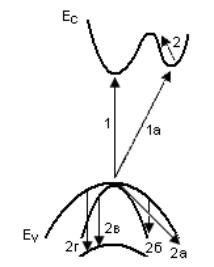
ражены на рисунке 5.2. На рисунке электронные и дырочные переходы изображены в ќ-пространстве.
Собственное поглощение света показано переходами 1 и 1а. Переходы 1 идут без существенного изменения волнового вектора электронов, и поэтому такое по-
глощение получило название прямого собственного поглощения. Переходы 1а идут с существенным изменением волнового вектора электронов (это изменение в герма-
нии и кремнии должно составлять величину порядка размеров зоны Бриллюэна, т. е.
ќ ≈ 108 см-1), и поэтому такое поглощение получило название непрямого собствен-
ного поглощения. В непрямом собственном поглощении обязательно участвуют фо-
ноны. Из рассмотрения переходов 1 – 1а ясно, что собственное поглощение невоз-
33
можно при энергиях квантов ћωфотон < Еg. Поэтому спектр собственного поглоще-
ния должен иметь спад, называемый краем собственного поглощения, в области ча-
стот фотонов ω≤ΔΕg/ћ.
Рисунок 5.2 – Электронные переходы в k-пространтсве при оптическом поглощении: 1 – прямое собственное поглощение; 1а – непрямое собственное
полощение; 2 и 2а – внутризонное поглощение свободными электронами и дырками; 2б, 2в и 2г – селективное поглощение свободными дырками
Переходы 2, 2а, 26, 2в, 2г, показанные на рисунке 5.2, происходят при погло-
щении световой энергии свободными носителями заряда в разрешенных зонах.
Внутризонные переходы 2 и 2а идут с изменением волнового вектора, что также требует участия фононов. Спектральная зависимость коэффициента поглощения для внутризонных переходов электронов и дырок имеет вид монотонной кривой и такое поглощение получило название неселективного (неизбирательного) поглощения свободными носителями. Селективное поглощение свободными носителями может идти без участия фононов и быть прямым. Исследования показывают, что вклад по-
глощения свободными носителями сильно возрастает в инфракрасной области спек-
тра.
34
Собственное поглощение при прямых переходах
Если при поглощении полупроводником кванта излучения имеет место возбуж-
дение электронов из валентной зоны в зону проводимости, то такое поглощение называют собственным или фундаментальным. При изучении собственного погло-
щения полупроводника следует учитывать строение его энергетических зон. Из-
вестные в настоящее время полупроводники в соответствии с конфигурацией энер-
гетических зон можно разделить на два основных вида. У первого из них минимум энергии в зоне проводимости, характеризуемый волновым вектором ќmin, и макси-
мум энергии в валентной зоне, определяемый волновым вектором ќmах, расположены в одной и той же точке зоны Бриллюэна (обычно в точке ќ = 0). Другими словами, у
этих полупроводников ќmin = ќmax (рисунок 5.2). В качестве примера полупроводника
стаким построением зон можно указать антимонид индия.
Увторого вида веществ экстремумы зоны проводимости и валентной зоны находятся при различных ќ, так что в этом случае ќmin≠ќmax. К последнему типу ве-
ществ относится большинство полупроводников, в том числе германий и кремний.
Переходы электронов через запрещенную зону будут происходить прежде все-
го между энергетическими состояниями, соответствующими максимуму валентной зоны и минимуму зоны проводимости, т. е. при значениях квазиимпульса р или вол-
нового вектора ќ, близких к нулю, как это показано на рисунке 5.2.
При взаимодействии электронов с фотонами должны выполняться два закона:
закон сохранения энергии и закон сохранения импульса. Если электрон до взаимо-
действия с фотоном, имеющим энергию ћω и импульс ћќф, обладал энергией Е и
квазиимульсом р, а после взаимодействия имел соответственно Е' и р', то эти законы запишутся в виде:
|
E , |
(5.17) |
E |
||
p p k . |
(5.18) |
|
|
Ф |
|
Импульс фотона ћќ очень мал по сравнению с квазиимпульсом электрона, так как длина волны света λф составляет 10-1÷10-5 см, а длина волны электрона в кри-
сталле при энергии электрона, соответствующей 300 К, равна примерно 5·10-7 см. В
связи с этим импульсом фотона можно пренебречь, поэтому:
35

p |
|
p |
|
(5.19) |
||
|
|
|||||
k |
|
k |
|
. |
(5.20) |
|
|
|
|
||||
Соотношение (5.19) или (5.20), называемое правилом отбора для электронных
переходов, показывает, что в процессе взаимодействия электрона кристалла с полем излучения возможны только такие переходы, при которых волновой вектор элек-
трона сохраняется. Эти переходы получили название вертикальных, или прямых,
переходов.
Рассмотрим собственное поглощение при прямых межзонных переходах для полупроводника, у которого зона проводимости и валентная зона обладают сфери-
ческой симметрией. Будем полагать, что валентная зона целиком занята электрона-
ми, а зона проводимости полностью свободна. Это условие справедливо для нелеги-
рованных полупроводников при 0 К.
Согласно рисунку 5.2 каждому начальному состоянию Е в валентной зоне при поглощении кванта света с энергией ћω отвечает такое конечное состояние Е' в зоне проводимости, что выполняется выражение (5.17).
В случае зон сферической симметрии:
|
|
|
|
|
k |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
E |
E |
C |
|
|
|
* |
; |
|
n |
|
|
2m |
|
||||
|
|
|
|
n |
|
|||
|
|
|
|
|
|
|
||
поэтому:
|
|
|
|
k |
|
|
|
|
|
2 |
|
|
2 |
E |
E |
|
|
|
* |
|
p |
V |
|
2m |
|||
|
|
|
p |
|||
|
|
|
|
|
||
,
(5.21)
|
|
|
|
k |
|
|
|
|
|
2 |
|
|
2 |
E |
g |
|
2m |
* |
||
|
|
|||||
|
|
|
n |
|||
|
|
|
|
|
||
,
(5.22)
где m* – приведенная масса электрона или дырки, определяемая соотношением:
|
|
|
n |
|
p . |
(5.23) |
1/ m |
* |
1/ m |
* |
1/ m |
* |
|
|
|
|
|
Коэффициент поглощения α(ћω) обратно пропорционален длине свободного пробега фотона lф, которая в свою очередь определяется скоростью движения фото-
на vф и временем его свободного пробега τф. Следовательно:
( ) |
|
l |
|
l |
|
l |
|
v |
|
||
|
Ф |
|
Ф |
||
|
|
|
Ф |
g( ) |
n |
|
c |
||
|
,
(5.24)
где g(ћω) = 1/τф – вероятность поглощения фотона в единицу времени; vф= c/n – скорость движения фотона в веществе;
36

n – показатель преломления вещества (действительная часть показателя);
с – скорость света в вакууме.
Количество поглощенных в единицу времени квантов света с энергией, лежа-
щей в интервале от ћω до ћ(ω +dω), пропорционально вероятности перехода элек-
тронов Р(ћω), числу квантовых состояний в валентной зоне в интервале энергии
|dЕ|:
g( )d ( ) 2P( )N (E) dE , |
(5.25) |
где коэффициент 2 учитывает два возможных направления поляризации света, N –
плотность квантовых состояний в валентной зоне.
Поэтому:
|
|
* |
3 / 2 |
|
||
g( ) |
(2m ) |
|
P( ) |
|||
|
2 |
|
3 |
|||
|
|
|||||
|
|
|
|
|||
E |
g |
|
1/ 2
.
(5.26)
Для прямых разрешенных переходов с сохранением квазиимпульса вероятность перехода Р(ћω) не зависит от энергии фотона. С учетом этого коэффициента соб-
ственного поглощения для прямых разрешенных переходов выражается формулой:
|
|
|
1/ 2 |
, |
|
A E |
g |
|
|
||
|
|
|
|
|
|
|
E |
|
|
||
0, |
|
|
|||
|
|
|
|
g |
|
|
|
|
|
|
|
E |
g |
|
,
(5.27)
где
|
|
2m m |
|
/ |
m |
|
m |
|
|
|
* |
* |
|
|
* |
* |
3 / 2 |
|
|
|
|
|
||||
A q |
2 |
n |
p |
|
|
n |
p |
|
|
|
|
2 |
|
* |
n |
|
|
|
|
|
|
|
|
|||
|
|
|
|
cm |
|
|||
|
|
|
|
|
|
n |
|
|
.
(5.28)
Соотношение (5.27) справедливо в ограниченном интервале изменения
(ћω – Еg). Как следует из рисунка 5.3, α2 линейно зависит от ћω в некотором интер-
вале. Продолжение этой прямой до пересечения с осью абсцисс позволяет опреде-
лить ширину запрещенной зоны Еg для прямых разрешенных переходов.
Из (5.27) следует, что для прямых переходов не должно иметь место поглоще-
ние квантов с энергией, меньшей ширины запрещенной зоны. В силу этого край собственного поглощения со стороны длинных волн (или малых энергий) должен быть очень резким.
37
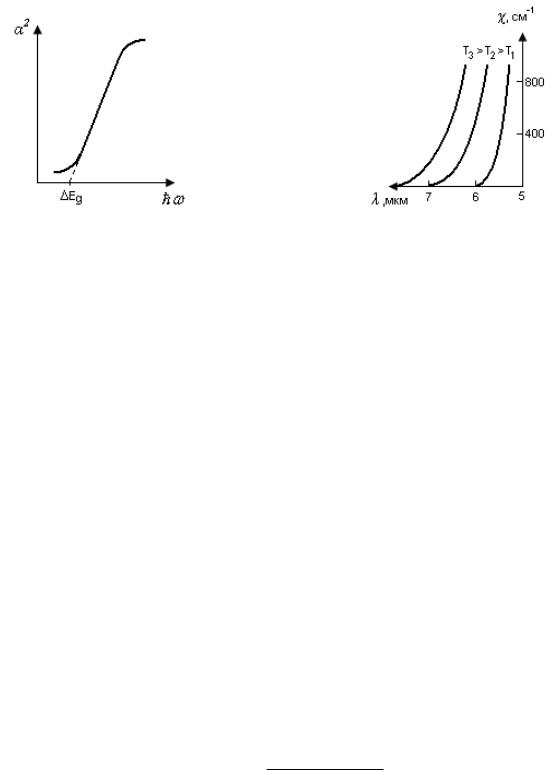
Рисунок 5.3 – Зависимость квадрата ко- |
Рисунок 5.4 – Спектр собственного по- |
эффициента поглощения при прямых |
глощения InS |
разрешенных переходах |
|
Действительно, как следует из рисунка 5.4, у очень чистого монокристалла ан-
тимонида индия, имеющего непараболичные зоны, наблюдается крутой рост погло-
щения.
Методика измерения собственного поглощения твердых тел
Коэффициент поглощения α рассчитывается по данным измерений прозрачно-
сти (коэффициента пропускания) образца:
T (1 R)2 |
1 ( a / 4 n)2 |
|
||
|
|
, |
(5.29) |
|
exp( d ) R2 |
|
|||
|
exp( d ) |
|
||
где n – показатель преломления материала, d – толщина пленки.
В области прозрачности от (1-R)/(1+R) до 10% для пропускания получается бо-
лее простая формула:
T
(1 R) |
2 |
exp( d ) |
|
|
|
|
|
1 R |
2 |
exp( 2 d ) |
|
|
|||
,
(5.30)
Когда Т<10%, формула приобретает вид:
T (1 R)2 exp( d) , |
(5.31) |
||||
откуда: |
|
|
|
|
|
|
1 |
|
(1 R)2 |
(5.32) |
|
|
|
|
|
|
|
|
|
||||
d |
Ln |
T |
. |
||
|
|
|
|
||
|
|
|
|
||
|
38 |
|
|
|
|

Для определения типа оптических переходов и ширины запрещенной зоны необходимо построить зависимость α1/2 = ƒ(ћω) и α2 = ƒ(ћω). Спрямление одной из этих зависимостей укажет на тип оптического перехода, а экстраполяция прямой к
α=0 даст величину Еg. Объектами исследований являются монокристаллы GaAs и Si. Измерения проводятся на спектрометре USB2000.
3. Экспериментальная установка USB2000
Для выполнения данной работы используется спектрометр USB2000 (рису-
нок 5.5).
Рисунок 5.5 – Спектрометр USB2000
Спектрометр USB2000 служит для измерения коэффициента пропускания (Т)
исследуемого образца в зависимости от длины волны света ( ). Коэффициент про-
пускания измеряется в процентах и определяется следующим образом:
T ( )
I ( ) |
||
I |
0 |
( ) |
|
|
|
100%
,
(5.33)
где I0( ) – интенсивность потока монохроматического излучения, падающего на измеряемый образец;
I( ) – интенсивность потока излучения, прошедшего через измеряемый образец.
Рассмотрим принцип действия спектрометра. В монохроматический поток из-
лучения (получаемой в оптической части прибора) на данной длине волны пооче-
редно вводятся контрольный и измеряемый образцы. За контрольный образец при-
39
нимается воздух и чистая кварцевая подложка (на такие же подложки нанесены ис-
следуемые пленки). При этом считается, что коэффициент пропускания контрольно-
го образца равен 100%. После введения контрольного образца, стрелка измеритель-
ного прибора устанавливается на 100% регулировкой ширины щели спектрометра.
Далее в поток излучения вводится измеряемый образец, и стрелка прибора отклоня-
ется пропорционально изменению светового потока. Величина коэффициента про-
пускания отсчитывается по шкале, отградуированной в процентах пропускания.
4. Порядок выполнения работы
Перед началом выполнения экспериментальной части необходимо внимательно изучить настоящее описание работы и ответить на контрольные вопросы.
Ознакомиться с экспериментальной установкой на принципиальной схеме и на макете.
Порядок работы:
1. Снять спектральную зависимость коэффициента пропускания Т(λ) для полу-
проводникового образца в диапазоне длин волн 320 – 900 нм, причем в диапазоне
320 – 500 нм с шагом 20 нм, а от 500– 900 нм с шагом 10 нм. Построить зависимость
Т(λ).
2. По краю поглощения на спектральной зависимости Т(λ) оценить ширину за-
прещенной зоны полупроводника.
3. Найти спектральную зависимость коэффициента поглощения α(λ) в диапа-
зоне длин волн 350 – 700 нм.
4.Построить зависимость α(λ) и экстраполируя линейную часть зависимости на ось длин волн по краю поглощения Урбаха, определить λ(граничная) поглощения и определить ширину запрещенной зоны полупроводника Eg.
5.Построить зависимость α2(λ) = f(hν). Оценить наличие линейного участка и межзонного оптического перехода. Экстраполируя линейную зависимость на ось абсцисс при α2(λ) = 0 определить ширину запрещенной зоны полупроводника Eg.
40
