203

дет доступа ни к одному из объемов памяти. Это четко видно на примере циклического списка (рис 8.10).

Рис. 8.10. Циклический список

Ни один из его счетчиков не является нулем, хотя никакие указатели на него извне не указывают. Этот объем памяти не восстановится никогда;

2)Обновление счетчиков ссылок представляет собой значительную нагрузку для всех программ. Это противоречит принципу Бауэра – «простые программы не должны расплачиваться за дорогостоящие языковые средства, которыми не пользуются».

недоступной, а тогда, когда программе требуется память в виде кучи или в виде стека, но ее нет в наличии. Таким образом, у программ с умеренной потребностью в памяти необходимость в ее высвобождении может не возникнуть. Тем программам, которым не хватает объема памяти в виде кучи, придется приостановить свои действия и затребовать недоступный объем памяти, а затем продолжить свою работу.

Процесс, высвобождающий память, когда выполнение программы приостанавливается, называется сборщиком мусора. В него входят две фазы.

Фаза маркировки. Все адреса (или ячейки), к которым могут обращаться идентификаторы, имеющиеся в программе, маркируются путем изменения бита в либо самой ячейке, либо в отображении памяти в другом месте.

Фаза уплотнения. Все маркированные ячейки передвигаются в один конец кучи (в дальний от стека).

Фаза уплотнения не тривиальна, так как она может повлечь за собой изменение указателей. Однако в общем случае она достаточно алгоритмически проста.

Самым критическим фактором является объем рабочей памяти, имеющийся у сборщика мусора. Будет нелогично, если самому сборщику мусора потребуется большой объем памяти. Кроме того, жела-

204

тельно, чтобы сборщик мусора был эффективен по времени. Естественно, что оба эти параметра одновременно оптимизировать невозможно, поэтому необходимо выбирать компромисс.

Нахождение ячеек, доступных для программы, связано с прохождением по древовидным структурам, так как ячейки могут содержать указатели на другие структуры. Необходимо пройти по всем путям, представленным этими указателями, возможно, по очереди, а «очевидное» место хранения указателей, по которым еще придется пройти, будет находиться в стеке. Именно это и входит в функции алгоритма маркировки.

Для простоты будем считать, что каждая ячейка имеет максимум два указателя, т.е. память представляется массивом структур вида

struct (int left, right, bool mark)

Поля left и right – это целочисленные указатели на другие ячейки; для представления нулевого указателя используется нуль.

Алгоритм маркировки можно представить в виде процедуры MARK1, которая использует переменные:

STACK – стек, используемый сборщиком мусора, для хранения указателей;

T – указатель стека, указывающий на верхний элемент;

А – массив структур с индексами, начиная с 1, представляющий кучу.

После того как все отметки покажут значение «ложь», ячейки, на которые непосредственно ссылаются идентификаторы в программе, маркируются, и их адреса помещаются вSTACK. Далее берется верхний элемент из STACK, маркируются непомеченные ячейки, на которые указывает ячейка, находящаяся по этому адресу, и их адреса помещаются в STACK. Выполнение алгоритма завершается, когда STACK оказывается пустым.

void proc MARK1; begin int k;

while T¹0

do k= STACK[T];

T minusab 1;

if left of A[k]¹0 and not mark of A[left of A[k]] then mark of A[left of A[k]]=true;

T plusab 1; STACK[T]=left of A[k]

fi;

if right of A[k]¹0 and not mark of A[right of A[k]] then mark of A[right of A[k]]=true;

T plusab 1; STACK[T]=right of A[k]

205

fi; od

end

До вызова этой процедуры куча могла иметь вид табл. 8.1, где маркировано только А[3], потому на него есть прямая ссылка идентифика-

Этот алгоритм очень быстрый, но крайне неудовлетворительный, во-первых, потому что может понадобиться большой объем памяти для стека, во-вторых, потому что объем требуемой памяти непредсказуем.

Другим крайним случаем является алгоритм, которому требуется небольшой фиксированный объем памяти, и не так важна эффективность по времени. Этот алгоритм представлен процедурой MARK2. Он нуждается в рабочей памяти для трех целых чисел: k, k1 и k2. Эта процедура просматривает всю кучу в поисках указателей от маркированных ячеек к немаркированным, маркирует последние и запоминает наименьший адрес ячейки, маркированной таким образом. Затем она повторяет этот процесс, начиная с наименьшего адреса, маркированного прошлый раз, и так до тех пор, пока при очередном просмотре не окажется ни одной новой маркированной ячейки.

void proc MARK2; begin int k, k1, k2;

k1=1; while k1£M

do k2= k1; k1=M+1; for k from k2 to M; do if mark then

if left of A[k]=0 and not mark of A[left of A[k]]; then mark of A[left of A[k]]=true;

k1=min(left of A[k], k1)

fi;

if right of A[k]¹0 and not mark of A[right of A[k]] then mark of A[right of A[k]]=true;

k1=min(right of A[k], k1)

206

fi

fi

od

od

end

Если этот алгоритм применяется в примере, который рассматривался для MARK1, то ячейки маркируются в том же порядке (5, 1, 2).

Оба эти алгоритма весьма неудовлетворительны (хотя и по разным причинам). Можно объединить их так, чтобы использовались преимущества каждого метода (алгоритм описан Кнутом).

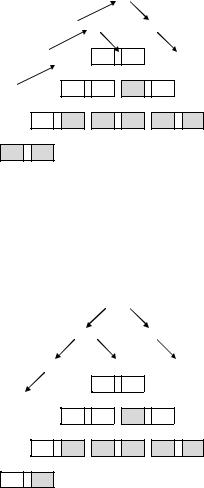
Вместо стека произвольного размера, как в MARK1, применяется стек фиксированного размера. Чем он больше, тем меньше времени может занять выполнение алгоритма. При достаточно большом стеке его скорость сопоставима со скоростьюMARK1. Однако, поскольку стек нельзя расширять, алгоритм должен уметь обращаться с переполнением, если оно произойдет. Когда стек заполняется, из него удаляется одно значение, чтобы освободить место для другого, добавляемого значения. Для запоминания удаленного таким образом из стека самого нижнего адреса используется целочисленная переменная(аналогично тому, что происходит в MARK2). Стек работает циклично с двумя указателями: один указывает вверх, другой вниз; это позволяет не пере-

мещать все элементы стека при удалении из него одного элемента

(рис. 8.11).

Верх

Низ

Рис 8.11. Стек с двумя указателями

Большей частью алгоритм работает какMARK1, и только когда стек становится пустым, завершает работу, если только из-за переполнения стека не были удалены какие-либо элементы. Если же элементы удалялись, то определяется самый нижний индекс, который «выпал» из стека, и именно с этого элемента начинается просмотр кучи. Этот процесс аналогичен процедуреMARK2. Любые другие адреса, которые нужно маркировать, помещаются в стек, и, если в конце просмотра он окажется пустым, алгоритм завершается. В противном случае алго-

207

ритм снова ведет себя какMARK1. Таким образом, алгоритм MARK3 действует аналогично процедуре MARK1, когда стек достаточно велик, и работает в смешанном режиме(MARK1 и MARK2) в противном случае.

Рис. 8.12. Бинарное дерево

Еще один подход предложен Шорром и Уэйтом. Он отличается тем, что в фазе маркировки структуры, по которым придется проходить, временно изменяются, обеспечивая пути возврата, чтобы можно было обойти все пути. Благодаря этому можно не использовать стек произвольного размера. Допустим, необходимо пройти по бинарному дереву, показанному на (рис. 8.12). К тому моменту времени, когда фаза маркировки достигнет нижней левой ячейки, это дерево будет выглядеть так, как изображено на (рис. 8.13).

Рис. 8.13. Бинарное дерево в конце обхода

алгоритма, пропорционально числу маркируемых ячеек.