Стандартная схема S в базисе B пуста (тотальна, свободна) тогда и только тогда, когда она пуста(тотальна, свободна) на множестве всех свободных интерпретаций этого базиса, т. е. если для любой свободной интерпретации Ih программа (S, Ih ) зацикливается (останавливается).
Стандартная схема S в базисе B свободна тогда и только тогда, когда она свободна на множестве всех свободных интерпретаций этого базиса, т. е. когда каждая цепочка схемы подтверждается хотя бы одной свободной интерпретацией.
1.3.4 Логико-термальная эквивалентность
Отношение эквивалентности E , заданное на парах стандартных схем, называют корректным, если для любой пары схемS1 и S2 из S1 E S2 следует, что S1 S2 , т. е. S1 и S2 функционально эквива-
лентны.
Построение таких (корректных и разрешимых) отношений связанно с введением понятия истории цепочки схем. В истории с той или иной степенью детальности фиксируются промежуточные результаты -вы полнения операторов рассматриваемой цепочки. Эквивалентными
объявляются схемы, у которых совпадают множества историй всех конечных цепочек.
Одним из отношений эквивалентности является логико-термальная эквивалентность (ЛТЭ).
|
Определим термальное значение переменной x для конечного пути |
||||
w схемы S |
как терм t (w, x) , который строится следующим образом. |
||||
1) |
Если путь w содержит только |
один операторA , то: |
t (w, x) = t , |
||
|
если A – оператор присваивания, |
t (w, x) = x , в остальных случаях. |
|||
2) |
Если w = w¢Ae , где A – оператор, e – выходящая из него дуга, |
||||
|
w¢ – непустой путь, ведущий к A , а x1 , x2 ,K, xn |
– все перемен- |
|||
|
ные t (Ae, x) , то |
|
|
|
|
|
t (w, x) = t (Ae, x) ëét (w¢, x1 ) x1 ,t (w¢, x2 ) x2 ,K,t (w¢, xn ) xn ûù . |
||||
|
Понятие |
термального значения |
распространим |
на |
произвольные |
термы t:
t (w, x) = t éët (w¢, x1 )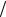
x1 ,t (w¢, x2 )
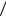x2 ,K, t (w¢, xn )
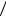xn ùû
Например, пути
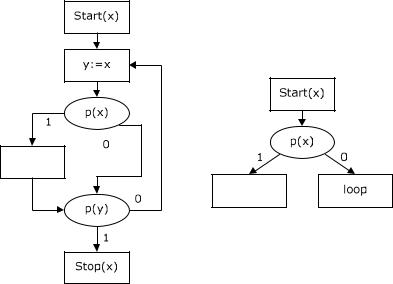
start(х); y:=x; p1(x); x:=f(x); p0(y); y:=x; p1(x); x:=f(x) в схеме на рисунке 1.5 а соответствует термальное значение f(f(x)) переменной х.
x:=f (x)
stop(f (x))
а |
б |
Рис. 1.5 |
определим еелогико- |
Для пути w в стандартной схемеS |
термальную историю (ЛТИ) lt (S,w) как слово, которое строится следующим образом.
1)Если путь w не содержит распознавателей и заключительной вершины, то lt (S,w) – пустое слово.
2) Если w = w¢ve , где v – распознаватель с тестом p (t1 ,t2 ,K,tn ), а e – выходящая из него D -дуга, D Î{0,1} , то
lt (S,w) = lt (S,w¢) pD (t (w¢,t1 ),t (w¢,t2 ),K, t (w¢,tn )).
3)Если w = w¢v , где v – заключительная вершина с оператором stop(t1, ..., tn), то
lt (S,w) = lt (S,w¢)t (w¢,t1 ),t (w¢,t2 ),K, t (w¢,tn )
Например, логико-термальной историей пути, упомянутого в приведенном выше примере, будет p1(x) p0(x) p1(f(x)).