
Статистическая теория радиотехнических систем.-3
.pdf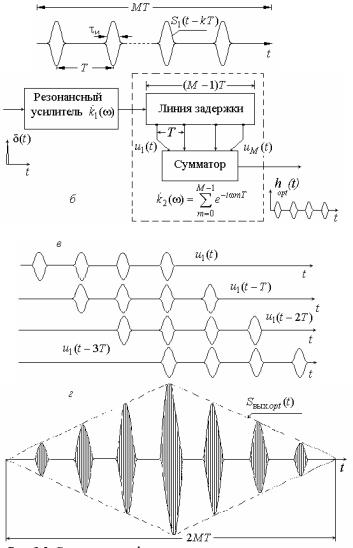
80
|
|
MT |
|
|
|
|
M −1 |
(n+1)T |
|
|
|
|
|
|
|
&( ) |
∫ |
( |
) |
e |
−iωt |
dt = ∑ |
∫ s1 |
( |
t − nT |
) |
e |
−iωt |
dt = |
|
|
g |
ω = |
s t |
|
|
|
|
|
|
|||||||
|
|
0 |
|
|
|
|
n=0 |
nT |
|
|
|
|
|
|
|
|
M |
−1 T |
|
|
|
|
|
|
M −1 |
|
|
|
|
|
|
|
= ∑ |
∫s1(x)e−iω(x+nT ) dx = g&1(ω) ∑ e−iωnT , |
(3.25) |
||||||||||||
|
n=0 |
0 |
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
ãäå g&1(ω) s1(t) |
— спектр одиночного импульса. Подставим в (3.10) |
||||||||||||||
общую длительность пачки t0 = τè + (M − 1)T и с учетом спектра пач-
ки (3.25) найдем коэффициент передачи оптимального фильтра в виде [9]
|
|
|
|
& |
|
|
& |
& |
(ω), |
|
|
(3.26) |
|
|
|
|
|
kopt |
(ω) = ck1 (ω) |
k2 |
|
|
|||||
& |
|
|
|
−iωτè |
|
& |
M −1 |
−iωmT |
|
1 − exp(−iωMT) |
|
|
|
k1 |
(ω) = g1 |
(ω)e |
|
, k2 |
(ω) = ∑ e |
|
|
= |
|
. |
(3.27) |
||
|
& |
|
|
|
|
|
|
|
|
|
1 − exp(−iωT) |
|
|
|
|
|
|
|
|
|
m=0 |
|
|
|
|
|
|
Первый сомножитель в (3.26) & (ω) есть коэффициент передачи k1
СФ для одиночного радиоимпульса. Каждое слагаемое второго сомножителя соответствует коэффициенту передачи звена, обеспечивающего задержку сигнала на время mT. Суммирование слагаемых по формуле суммы конечного числа элементов геометрической про-
грессии дает выражение (3.27). Таким образом, & (ω) есть коэффи- k2
циент передачи многоотводной линии задержки с суммированием задержанных сигналов. Общее время задержки в линии (M−1)T. Структурная схема СФ для пачки радиоимпульсов, соответствующая формуле (3.26), показана на рис. 3.5,б. При подаче на вход СФ δ-импульса на выходе сумматора получается последовательность М (по числу отводов) радиоимпульсов, каждый из которых по форме повторяет импульсную реакцию фильтра, согласованного с одиноч- ным импульсом пачки. На рис. 3.5,в условно показан процесс оптимальной фильтрации пачки из М = 4 импульсов с симметричной огибающей гауссовой формы. Огибающая пачки радиоимпульсов на выходе сумматора Sâûõopt(t) имеет треугольную форму, длительность по нулям 2МТ и число импульсов (2М−1).
Рассмотрим частотную интерпретацию работы СФ-пачки.
81
à
Рис. 3.5. Согласованная фильтрация пачки когерентных радиоимпульсов гауссовой формы: а — пачка импульсов; б — структура СФ для пачки;
â— последовательности импульсов на выходах линии задержки
èсумматора (M=4); г — радиоимпульсы на выходе сумматора

82
Определив из (3.27) модуль |
& |
, найдем АЧХ второго звена |
||||||
k2 (ω) |
||||||||
ÑÔ â âèäå [12] |
|
|
|
|
|
|
|
|
K2 ( f ) = |
|
sin(πf MT ) |
|
|
. |
(3.28) |
||
|
|
|||||||
|
|
sin(πf T ) |
|
|||||
|
|
|
|
|
|
|||
Частотная характеристика (3.28) является гребенчатой (рис. 3.6,а) с периодически повторяющимися через интервал 1/Т зубцами, ширина которых по нулям 2/(МТ). В случае идеальной линии задержки АЧХ (3.28) существует на всей оси частот. Результирующая АЧХ
K ( f ) = K1( f ) K2 ( f ) практически ограничена по спектру колокольной (гауссовой) характеристикой K1(f) фильтра, согласованного с одиночным импульсом пачки. Очевидно, что отношение сигнала к шуму по мощности в момент максимума сигнала на выходе СФ равно
2E1M |
= |
2Eпачки |
, |
(3.29) |
|
|
|||
N0 |
|
N0 |
|
|
что соответствует результатам подраздела 3.2.
Рис. 3.6. Гребенчатая АЧХ схемы оптимального суммирования (а) и результирующая АЧХ (б) для когерентной пачки радиоимпульсов
Напомним, что выигрыш в отношении сигнала к шуму получается за счет синфазного суммирования импульсных колебаний сигнала в определенный момент времени. Спектральные составляющие шума суммируются со случайными фазами. Гребенчатая структура АЧХ
СФ, совпадающая со структурой амплитудно-частотного спект-
83
ра когерентной пачки импульсов, обеспечивает прохождение через СФ только части спектральных составляющих помехи. Наименьшее усиление СФ имеет на тех участках спектра, где уровень сигнальных составляющих мал.
3.4.Обнаружение и различение сигналов при наличии помех (байесов метод)
Статистическая теория принятия решений при наличии помех вклю- чает два основных раздела: первый — статистическая теория про-
верки гипотез и второй — статистическая теория оценок неизвес-
тных параметров. Для решения задач оптимального обнаружения, различения и классификации сигналов применяют аппарат статисти- ческой теории проверки гипотез. В 30-х годах прошлого века американский математик Джон Нейман и английский математик Карл Пирсон заложили основы теории проверки гипотез.
Рассмотрим две наиболее простые задачи, связанные с бинарным различением и обнаружением сигналов. В этом случае в приемнике реализуется алгоритм принятия решения в пользу одной из двух возможных гипотез: H0 èëè H1. В цифровых РСПИ эти гипотезы соответствуют передаче по каналу связи на интервале [0;T] одного из двух полезных сигналов s0(t,λ0) èëè s1(t,λ1). В РЛ- и РН-системах при решении задачи обнаружения гипотеза H0 означает отсутствие полезного сигнала, т.е. s0(t,λ) = 0. Таким образом, задача различения является более общей. Рассмотрим эту задачу и применим для ее решения байесов метод [13], основоположником которого является американский математик Вальд А.
Постановка задачи. Наблюдаемый сигнал на входе приемника представим в виде
y(t) = θ F [s1(t,λ1);n(t)]+ (1− θ) F [s0 (t,λ0 ); n(t)]; t [0;T ], (3.30) где θ — случайная величина с двумя значениями 0 и 1;
F [si (t,λi (t); n(t)] — оператор, определяющий способ взаимодействия
полезного сигнала s( ) и помехи n(t).
Априорные вероятности значений случайной величины θ известны: P(θ = 0) = p0 è P(θ = 1) = p1. Статистические свойства помехи и сигналов предполагаются также заданными. Таким

84
образом, при дискретном отборе данных на интервале [0;T] могут быть определены n-мерные условные ПРВ (подраздел 1.4)
W ( y1, y2 ,K, yn H0 ) = W (y H0 ), |
|
W ( y1, y2 ,K, yn H1 ) = W (y H1 ), |
(3.31) |
ãäå Í0 è Í1 — две случайные гипотезы (события), соответствующие двум возможным состояниям наблюдаемого сигнала. Оптимальный различитель на основе обработки сигнала y(t) должен лучшим способом принять решение о том, какая из двух гипотез реализовалась в конкретном наблюдении. Фактические данные наблюдений в статистике называют выборкой; в данном случае это n-мерный вектор
y = {y1, y2 ,..., yn }, ãäå yi = y(ti ), i = 1,K,n.
Решение задачи. Очевидно, система различения из-за влияния помех может случайно оказаться в одной из четырех ситуаций.
1. Состояние на входе — верна гипотеза H1.
Состояние на выходе (решение) — верна гипотеза ˆ .
H1
2. Состояние на входе — верна гипотеза Н1.
Состояние на выходе (решение) — верна гипотеза ˆ .
H0
3. Состояние на входе — верна гипотеза H0.
Состояние на выходе (решение) — верна гипотеза ˆ .
H0
4. Состояние на входе — верна гипотеза H0.
Состояние на выходе (решение) — верна гипотеза ˆ .
H1
Видно, что ситуации 1 и 3 соответствуют правильному различению сигналов, а 2 и 4 — ошибочному.
Для определения количественного критерия эффективности раз-
личения назначим плату за результат работы системы. Очевидно, плата зависит от состояния на входе и выходе и определяется потерями, которые несет «лицо», использующее результаты различения сигналов. Введем платежную матрицу
Выход |
|
Âõîä |
C = {Cij}; где i,j = 0,1; первый ин- |
|
|
|
|
||
|
H0 |
|
H1 |
декс определяет принятую гипотезу |
ˆ |
C00 |
|
C01 |
на выходе (решение), второй — ги- |
H0 |
|
потезу на входе. Без потери общно- |
||
H1 |
C10 |
|
C11 |
|
|
сти рассуждений будем полагать |
|||
ˆ |
|
|
|
|
|
|
|
|
плату за ошибки положительной, |
ò.å. C10, C01 > 0, и за верные решения C00, C11 ≤ 0. Элементы Cij записаны в таблицу.
85
Критерий оптимальности различителя. В качестве критерия используем величину средней платы, т.е. ее математическое ожидание потерь. В теории принятия решений эту величину называют средним байесовым риском R. По правилу вычисления среднего дискретной случайной величины С получим
R = M[C] = C00 P (H0 |
H |
0 ) + C11P(H1 |
H1 ) + |
||
|
|
|
ˆ |
|
ˆ |
|
ˆ |
|
|
ˆ |
(3.32) |
+ C01P (H1 H |
0 ) + C10 P(H0 H1 ), |
||||
ˆ |
ˆ |
Hi ) |
— вероятность совместного по- |
||
ãäå P(Hi H j ) = P(Hi ) P(H j |
|||||
явления событий Hi |
ˆ |
ˆ |
Hi ) — условная вероятность при- |
||
è H j ; P(H j |
|||||
нять решение |
ˆ |
в предположении, что на входе верна гипотеза Hi. |
H j |
Для наглядности дальнейших рассуждений используем геометрическую интерпретацию задачи. На рис. 3.7 условно показано
n-мерное евклидово пространство |
|
|
|
|
|
|
|
|
|
|
|
с осями координат oνi (i = 1 ÷ n) . |
|
|
|
|
|
|
|
|
|
|
|
Множество возможных выбороч- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ(y)=γ 0 |
||
|
|
|
|
|
|
|
Y1 |
|
|||
ных значений y обозначим Y |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
(иногда его называют простран- |
|
|
|
|
|
||||||
|
Y0 |
|
|
|
|
||||||
ством наблюдений). Любому вы- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
борочному вектору y Y соответ- |
|
|
|
|
|
|
|
|
|
|
|
ствует точка с координатами |
|
|
|
|
y |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
Y=Y1 Y0 |
|
|
|
|
|||||
(ó1,ó2,…,ói…,ón). Îäíà èç íèõ yi ïî- |
|
|
|
||||||||
Рис. 3.7. Пространство наблюдений |
|||||||||||
казана на рисунке. |
|||||||||||
Очевидно, что решающее правило в бинарном случае сводится к тому, чтобы найти способ разбиения множества Y на сумму двух непересекающихся подмножеств Y0 è Y1, ò.å. Y = Y0 Y1. И далее,
åñëè y Y0, то принимается решение |
ˆ |
; åñëè y Y1, то принима- |
H0 |
ется решение |
ˆ |
. Конкретное разбиение в n-мерном пространстве |
H1 |
определено заданием уравнения поверхности, которое, в общем слу- чае, имеет вид γ(y1, y2, ..., yn) = γ0, ãäå γ0 = const. Таким образом, для всех y Y0 выполняется неравенство γ(y) < γ0 è äëÿ y Y1 соответственно γ(y) > γ0. Задача состоит в том, чтобы найти оптимальное решающее правило: функцию γopt(y) и ее пороговое значение —

86
величину γ0. Заметим, что любое преобразование наблюдаемых данных в статистических задачах называют статистикой.
Важно отметить, что статистика γopt(y) осуществляет редукцию исходных данных: на входе «наблюдатель» располагает n-мерным вектором y, который содержит информацию о переданном сигнале; на выходе после обработки получена скалярная величина γ. Очевидно, что при таком взаимно неоднозначном преобразовании первичная информация, в общем случае, может быть частично утрачена. Удивительно, однако, то, что существуют такие статистики (их называют
достаточными), которые, несмотря на редукцию первичных данных, не ведут к потере полезной информации, содержащейся в них. Интуитивно понятно, что оптимальное решающее правило должно бы обладать этим замечательным свойством.
Оптимальное решающее правило найдем из условия минимума среднего риска (МСР) (3.32). Запишем выражения для условных вероятностей в виде интегралов от соответствующих n-мерных условных ПРВ по области Y0:
ˆ |
H0 ) = ∫... ∫ ∫ ∫W ( y1,..., yn / H0 ) dy1 dy2...dyn , |
|
|
|
P(H0 |
|
|
|
|
|
Y0 |
|
|
|
|
|
|
|
|
ˆ |
H0 ) = 1 − ∫... ∫ ∫ ∫W ( y1,..., yn / H0 ) dy1 dy2 ...dyn |
|
|
|
P(H1 |
, |
|
||
|
Y0 |
|
|
(3.33) |
ˆ |
H1 ) = ∫... ∫ ∫ ∫W ( y1 ,..., yn / H1 ) dy1 dy2 ...dyn , |
|
|
|
|
|
|
||
P(H0 |
|
|
||
|
Y0 |
|
|
|
ˆ |
H1 ) = 1− ∫... ∫ ∫ ∫W ( y1 ,..., yn / H1 ) dy1 dy2 ...dyn. |
|
|
|
|
|
|||
P(H1 |
|
|||
|
Y0 |
|
|
|
|
|
|
|
|
Подставив выражения (3.33) в формулу (3.32), после группирования слагаемых с учетом того, что Р(Н0) = ð0 è Ð(Í1) = ð1, получим
∫ |
∫ ∫ ∫ 1 01 |
R = p0C10 + p1C11 + |
|
|
|
|
|
|
|
|
(3.34) |
|||
11 |
y |
1 0 |
10 |
|
00 |
|
y |
|
0 |
y |
||||
+ ... |
p (C |
− C )W ( |
H )− p |
(C |
− C |
|
)W ( |
H |
|
|
|
|||
|
|
|
|
) d . |
|
|||||||||
Y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первые два слагаемых в (3.34) постоянны и от выборки y не зависят.Подынтегральноевыражениеприлюбых y естьразностьположительных величин, поскольку C01 > C11, C10 > C00 и условные функ-
87
öèè ÏÐÂ W (y Hi ) ≥ 0 . Таким образом, минимум среднего риска (3.34) можно обеспечить, если для всех y Y0 выполняется условие
Hi ) ≥ 0 . Таким образом, минимум среднего риска (3.34) можно обеспечить, если для всех y Y0 выполняется условие
p |
(C |
− C |
)W (y H |
1 |
) − p |
(C |
− C |
00 |
)W (y H |
0 |
) < 0. |
(3.35) |
|
|
1 |
01 |
11 |
|
0 |
10 |
|
|
|
|
|||
Преобразуя неравенство (3.35) так, чтобы в правой части оказа-
|
|
|
|
|
|
|
ˆ |
лись постоянные величины, получим правило принятия решения H0 |
|||||||
γopt |
(y) = |
W (y H1 ) |
|
< |
p0 (C10 − C00 ) |
. |
(3.36) |
|
|
||||||
|
W (y H0 ) |
|
p1 (C01 − C11 ) |
|
|||
Таким образом, оптимальный различитель 2-х сигналов обрабаты-
вает наблюдаемый сигнал y и формирует на выходе решение: |
|
||||||||
ˆ |
|
|
W (y H1 ) |
|
|
|
|||
H1, åñëè |
γopt |
(y) = |
|
|
|
|
> γ0 ; |
|
|
W (y H0 ) |
|
||||||||
|
|
|
|
|
(3.37) |
||||
|
|
|
|
W (y H1 ) |
|
|
|
||
ˆ |
γopt |
(y) = |
|
< γ0 |
|
|
|||
H0 , åñëè |
W (y H0 ) |
, |
|
||||||
|
|
|
|
|
|
||||
где оптимальный порог γ0 = p0 (C10 – C00 ) p1 (C01 – C11 ).
p1 (C01 – C11 ).
Смысл отношения условных ПРВ в (3.37) состоит в том, что оно пропорционально отношению соответствующих вероятностей. Вычислив его для конкретной выборки y, различитель «может судить» о том, какая из 2-х гипотез более правдоподобна. По этой причине функцию γopt(y) в специальной литературе называют отношением правдоподобия и обозначают, как правило, L(y), что связано с английским словом likеlihood — правдоподобие.
Структура устройства, которое реализует оптимальный алгоритм различения сигналов, определяется конкретным видом условных ПРВ.
3.5.Другие критерии оптимальности обнаружения
èразличения
Можно предположить, что в зависимости от критерия оптимальности может измениться правило принятия решения, т.е. способ обработки входного сигнала. Во всяком случае, повседневный опыт это подтверждает. Например, от критерия оценки работы сотрудника зависит стратегия его поведения. Покажем, что байесов критерий (МСР)

88
является вполне общим, т.е. к нему сводятся другие не менее целесообразные критерии. Предварительно представим (3.32) для величины R в виде
ˆ |
|
ˆ |
H1 ) + |
|
R = C00 p0 P (H0 |
H0 ) + C11 p1 P(H1 |
|
||
ˆ |
H1 ) |
ˆ |
H0 ). |
(3.38) |
+C01 p1 P (H0 |
+ C10 p0 P (H1 |
|||
Критерий минимума взвешенной вероятности ошибки. Выше отмечалось, что в бинарной задаче проверки гипотез возможны 4 исхода, из которых два ошибочных и два верных. В теории проверки гипотез ошибкой 1-го рода называют случайное событие, состоящее
в том, что система принимает решение |
ˆ |
в пользу гипотезы H1, |
H1 |
||
в то время как верна гипотеза H0. Вероятность этой ошибки |
||
ˆ |
|
ˆ |
P(H1  H0 ) . Ошибка 2-го рода состоит в появлении события H0 ïðè
H0 ) . Ошибка 2-го рода состоит в появлении события H0 ïðè
условии, что верна гипотеза |
ˆ |
H1 ) . |
H1. Вероятность этой ошибки P(H0 |
Очевидно, что вполне разумной является стратегия минимизации взвешенной вероятности ошибочных решений. Критерий тогда определяется величиной
ˆ |
ˆ |
H1 ), |
(3.39) |
Kîø = k1 P(H1 |
H0 ) + k2 P(H0 |
ãäå k1 è k2 — весовые коэффициенты, зависящие от потерь, которые возникают вследствие допущенных ошибок. Сравнивая (3.38) и (3.39),
видно, что величина Kîø = R, åñëè C11 = C00 = 0 è k1 = p0C10, k2 = p1C01. Следовательно, данный критерий есть частный случай кри-
терия МСР.
Критерий идеального наблюдателя. Критерий состоит в том, что в системе принятия решений необходимо обеспечить минимум полной вероятности ошибочных ситуаций. В соответствии с форму-
лой полной вероятности имеем |
|
|
H1 ). |
|
ˆ |
H |
ˆ |
(3.40) |
|
Pîø = p0 P(H1 |
0 ) + p1 P(H0 |
Идеальный наблюдатель полагает p0 = p1 = 0,5. По существу, это весовой критерий, когда k1 + k2 = 1 и обе ошибки одинаково опасны. Подобная ситуация характерна для различения сигналов в цифровых системах связи, где s0(t) è s1(t) используются для передачи нуля и единицы. Таким образом, этот критерий также следует из критерия МСР.
89
Критерий Неймана — Пирсона. Для РЛ-систем характерна ситуация, когда сигнал s0(t) = 0, т.е. необходимо различать две гипотезы: H0 — на входе только шум (в зоне обзора цели нет) и H1 — на входе РЛ-приемника есть сигнал s1(t). Как правило, вероятности p0 è p1 (отсутствия и наличия цели) неизвестны. Вероятность же ошиб-
êè 1-ãî ðîäà |
ˆ |
H0 ) = F (fals), называемая вероятностью лож- |
P(H1 |
ной тревоги, не должна превосходить заранее заданного значения. Оптимальный РЛ-приемник обнаружения должен обеспечить мак-
ˆ |
ˆ |
H1 ) = D (detection) — âå- |
симальную величину P(H1 |
H1 ) = 1− P(H0 |
роятности правильного обнаружения при заданной величине F. Это условие носит название критерия Неймана — Пирсона. Данный критерий также следует из критерия МСР как частный случай [1].
Таким образом, для всех перечисленных выше критериев способ обработки остается неизменным, т.е. оптимальный различитель (обнаружитель) формирует величину L(y) — отношение правдоподобия.
Отличие устройств обработки состоит в выборе стоимостей за принятые решения, которые влияют только на порог γ0.
3.6.Различение двух детерминированных сигналов на фоне белого гауссова шума. Структура оптимальных устройств
Пусть наблюдаемый сигнал y(t) содержит в качестве помехи аддитивный собственный шум приемника. Тогда выражение (3.30) принимает следующий конкретный вид:
y(t) = θ s1(t, λ1) + (1 − θ) s0 (t,λ0 ) + n(t), t [0,T ]. (3.41) Будем считать, что полезные сигналы s0(t) è s1(t) являются детерминированными. Важное условие, при котором решаем задачу,
состоит в том, что предполагаются точно известными моменты
начала и окончания временного интервала, в котором находится полезный сигнал s(t). Неизвестно лишь то, какой это сигнал: s0(t) èëè
s1(t).
Гауссов белый стационарный шум n(t) имеет нулевое среднее зна- чение и корреляционную функцию Kn (τ) = (N0  2) δ(τ) .
2) δ(τ) .

90
Определим в явном виде отношение правдоподобия (3.37) для дискретной выборки из наблюдаемого сигнала (3.41). Для двух гипотез на входе приемника имеем
H0 θ = 0 : |
yi = s0i + ni ; |
i = 1,..., m; |
H1 θ = 1: yi = s1i |
+ ni , ãäå s0i |
= s0 (ti ), ni = n(ti ). (3.42) |
Будем считать, что энергетический спектр шума сосредоточен в полосе ± fâ. Тогда при интервале дискретизации ∆t = 1 2 fâ согласно рис. 1.18 отсчеты гауссова шума статистически независимы. Дисперсия шума σ2n = N0 fâ = N0
2 fâ согласно рис. 1.18 отсчеты гауссова шума статистически независимы. Дисперсия шума σ2n = N0 fâ = N0  (2∆t) . Регулярный сигнал выполняет роль среднего значения: H0 : yi = s0i ; H1 : yi = s1i . С учетом (1.42) m-мерные условные ПРВ выборочного вектора y для двух гипотез имеют вид:
(2∆t) . Регулярный сигнал выполняет роль среднего значения: H0 : yi = s0i ; H1 : yi = s1i . С учетом (1.42) m-мерные условные ПРВ выборочного вектора y для двух гипотез имеют вид:
H |
|
: |
W (y H |
|
) = |
|
1 |
|
|
|
1 |
|
m |
(y |
− s |
|
|
|
|
|
|
|
exp − |
|
∑ |
)2 ; |
|
||||||||||
|
0 |
|
|
0 |
|
σm (2π)m / 2 |
|
|
2σ2 |
i |
0i |
|
|
|
||||
|
|
|
|
|
|
n |
|
|
|
|
n |
i=1 |
|
|
|
(3.43) |
||
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
W (y H1 ) = |
|
|
|
|
m |
|
|
|
|
||||||
H1 : |
|
|
|
exp − |
|
|
|
∑( yi |
− s1i )2 , |
|
|
|||||||
σm |
(2π)m / 2 |
2σ2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
n |
|
|
|
|
n |
i=1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ãäå m = T/∆t — число отсчетов на интервале наблюдения. Подставляя (3.43) в (3.37), после выполнения простых алгебраических преобразований получим
|
|
∆t |
|
|
m |
|
m |
|
|
2∆t |
|
m |
|
|
L(y) = exp |
− |
|
|
∑ s12i − ∑ s02i |
exp |
|
∑ yi (s1i − s0i ) . |
(3.44) |
||||||
|
|
|||||||||||||
|
|
N0 |
|
i |
= |
i |
= |
|
|
N0 |
i |
= |
|
|
|
|
|
1 |
1 |
|
|
1 |
|
|
|||||
Выражение (3.44) определяет искомое отношение правдоподобия для задачи различения 2-х сигналов с полностью известными параметрами на фоне помехи в виде квазибелого шума. Оно допускает простой предельный переход к случаю белого шума, когда fâ → ∞, à ∆t → 0. При этом суммы в показателе степени первого сомножителя перейдут в интегралы, численно равные энергии различаемых сигналов:
m 2 lim ∑ s1i
∆t→0 i=1
m 2 lim ∑ s0i
∆t→0 i=1
∆t =
∆t =
T
∫ s12 (t, λ1)dt
0
T
∫ s02 (t,λ0 )dt
0
= Es1(λ1) ,
(3.45)
= Es0 (λ0 ).
91
Сумма в показателе второго сомножителя перейдет в интеграл
|
m |
|
T |
T |
lim |
∑( yi s1i |
− yi s0i ) ∆t = ∫ y(t)s1(t, λ1) dt − ∫ y(t)s0 (t, λ0 ) dt. (3.46) |
||
∆t→0 i=1 |
|
0 |
0 |
|
Полагая, что энергия сигналов Es1 è Es0 не зависит от параметра λ, отношение правдоподобия окончательно может быть представлено в виде
|
|
|
|
|
|
Es1 − Es0 |
|
|
|
|
|
L[y(t)]= exp |
− |
|
|
|
|||||||
|
|
||||||||||
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
2 |
T |
|
|
|
|
|
|
|
|
|
exp |
∫ |
y(t)[s |
(t, λ |
) − s (t,λ |
|
)]dt . |
(3.47) |
||||
|
0 |
||||||||||
|
|
1 |
|
1 |
0 |
|
|
|
|||
|
N0 0 |
|
|
|
|
|
|
|
|
|
|
Предельная форма (3.47) отношения правдоподобия (3.44) называется функционалом отношения правдоподобия. Процедура разли- чения сигналов, состоящая в сравнении L[y(t)] с порогом γ0, может быть заменена испытанием любой монотонной функции от этого отношения на соответствующий порог. Упрощение алгоритма оптимального различения достигается после логарифмирования (3.47). Выполнив его, оставим в левой части решающего правила (3.37) слагаемые, зависящие от наблюдаемой реализации y(t). В итоге оптимальное правило различения принимает следующий вид:
|
|
|
|
|
|
H1 |
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
2 |
T |
2 |
T |
> |
zÏ |
|
|
||
z = |
|
∫ y(t) s1(t, λ1) dt − |
|
∫ y(t) s0 (t, λ0 ) dt |
ˆ |
|
, |
(3.48) |
|
|
N0 |
|
|||||||
N0 |
0 |
0 |
|
H0 |
|
|
|||
|
|
|
|
< |
|
|
|||
|
|
|
|
|
|
zÏ |
|
||
|
|
zÏ = ln γ0 + (Es1 − Es0 ) |
N0 , |
|
|
|
(3.49) |
||
ãäå zÏ — модифицированный порог.
Структура каждого из интегралов в (3.48) совпадает со структурой выражения (1.15а), определяющего корреляционную функцию. По этой причине приемное устройство, реализующее для различения двух полностью известных сигналов алгоритм вида (3.48), называют
корреляционным приемником.
Из (3.48) следует, что для вынесения решения о наличии на входе приемникасигнала s1(t,λ1) èëè s0(t,λ0) необходимореализацию y(t) перемножить с копией каждого из ожидаемых сигналов, проинтегрировать произведение, вычесть выходные сигналы интеграторов

92
âмомент t = T и результат сравнить с порогом. Если пороговый уровень превышен, то принимается решение о наличии на входе s1(t);
âпротивномслучае—решениеоналичии s0(t). Длякритерияидеальногонаблюдателяипривеличинахэнергии Es1 = Es0, чтоимеетместо, например,приЛЧМиФКМ,порог zÏ = 0. Таким образом, оптимальный приемник фактически принимает решение по знаку разности выходных сигналов интеграторов. На рис. 3.8,а показана структурная схемаоптимальногоразличителя,соответствующаяалгоритму(3.48). Генераторы опорного сигнала (ГОС) формируют копии ожидаемых сигналов;устройствосинхронизации(УС)обеспечиваеттактирование работы различителя — запуск ГОС и считывание уровней сигналов
|
|
2 |
T |
2 |
T |
|
|
z1 |
= |
∫ y(t) s1(t,λ1) dt, z0 = |
∫ y(t) s0 (t,λ0 ) dt |
(3.50) |
|||
|
|
||||||
|
|
N0 0 |
N0 0 |
|
|||
с выхода интеграторов в момент t = T.
à |
á |
Рис. 3.8. Структурные схемы оптимальных различителей: вариант с корреляционной обработкой (а);
вариант с применением согласованных фильтров (б)
Сравнивая (3.50) и (3.17), видно, что величины z1 è z0 можно получить как выходной сигнал z(t) СФ в момент времени t = t0. Структурная схема различителя с использованием СФ приведена на рис. 3.8,б; синхронизатор обеспечивает сравнение выходных напряжений СФ в момент времени t = T. Задача, рассмотренная выше, типична для цифровых систем передачи информации.
Напомним, что в РЛ- и РН-системах гипотезе H0 соответствует ситуация, когда y(t) = n(t), т.е. объекта в зоне обзора нет и на входе приемникаприсутствуеттолькособственныйшум.Очевидно,чтоструктура оптимального РЛ-обнаружителя является частным случаем различителя. Алгоритм обработки в этом случае содержит один канал.
93
3.6.1.Статистическиехарактеристикикачестваразличения
Критерий качества решения задачи различения определен выражением (3.40). Вероятности двух ошибочных решений для критерия идеального наблюдателя (порог zÏ = 0) согласно (3.48) равны
ˆ |
|
∞ |
0 |
|
|
ˆ |
H1 ) = ∫ W (z H1 )dz, |
(3.51) |
|
P(H1 |
H0 ) = ∫W (z H0 ) dz, P(H0 |
|||
|
|
0 |
−∞ |
|
ãäå W (z H1 ) |
è W (z H0 ) — условные ПРВ сигнала z = z1–z0 |
íà âû- |
||
ходе разностного блока (3.48), (3.50). Если на входе верна гипотеза H1, то случайная величина сигнала на выходе различителя
|
2 |
T |
|
|
z = |
∫[s1 (t) + n(t)] [s1 (t) − s0 (t)] dt. |
(3.52) |
||
N |
||||
|
0 |
|
||
|
|
|
Являясь линейным преобразованием гауссова шума, величина z также будет гауссовой. Расчет условного среднего значения и условной дисперсии величины z выполним по способу, который использовался при выводе (3.21). В итоге получим:
M[z H1 ] = |
2Es |
(1 − ks ), |
Dz H |
|
= |
4Es |
(1 − ks ), |
(3.53) |
|||
|
1 |
|
|||||||||
|
N0 |
|
|
|
|
|
|
N0 |
|
||
где величина |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
|
|
|
|
|
|
ks |
= |
∫ s1(t) s0 (t) dt |
(3.54) |
|||||||
|
|
||||||||||
|
|
|
|
Es 0 |
|
|
|
|
|
|
|
является по смыслу коэффициентом взаимной корреляции между
сигналами s1(t) è s0(t).
Если на входе верна гипотеза H0, то случайная величина
|
|
|
2 |
T |
|
|
|
|
|
|
|
|
|
|
|
||||
z = |
|
∫[s0 (t) + n(t)] [s1(t) − s0 (t)]dt . |
|
|
(3.55) |
||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
N |
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Она имеет гауссову ПРВ с параметрами |
|
|
|
|
|
|
|||||||||||||
M[z H |
0 |
] = − |
|
2Es |
(1 − k |
s |
) |
è |
D |
z H0 |
= |
4Es |
(1− k |
s |
). |
(3.56) |
|||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
N0 |
|
|
|
|
N0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Условные ПРВ W(z/H1) è W(z/H0) показаны на рис. 3.9. Полная вероятность ошибочного различения сигналов для «идеального наблюдателя» равна
P |
∞ |
W (z H |
|
)dz |
+ |
0 |
W (z H |
|
|
(3.57) |
|
= 0,5 |
∫ |
|
∫ |
|
)dz . |
||||||
îø |
|
|
0 |
|
|
|
1 |
|
|
||
|
|
0 |
|
|
|
|
−∞ |
|
|
|
|

94
Вероятности двух ошибок различения (3.51) численно равны площадям областей, которые на рис. 3.9 заштрихованы. Интегрирование в (3.57) гауссовых ПРВ сводится, как известно, к интегралу вероятности Ф(х). В итоге после вычислений получим
Pîø = 1 − Ô ( (Es N0 ) (1 − ks ) ). |
(3.58) |
MM
Рис. 3.9. Гауссова плотность распределения вероятностей сигнала z для двух гипотез: H1 — наличие сигнала s1(t); H0 — наличие s0(t)
Интеграл вероятности Ф(х) являетсямонотонновозрастающей функцией аргумента. Поэтому при заданном отношении сигнала к шуму наибольшую помехоустой- чивость (меньшую вероятность ошибки) будут иметь сигналы, для которых коэффициент взаимной корреляции минимален. Величи- на ks изменяется от –1, когда
s1(t) = −s0(t) (противоположные сигналы), до +1, когда s1(t) =
= s0(t). В случае, когда ks = 0, говорят, что сигналы ортогональ-
ны. Одинаковые сигналы (ks = 1), очевидно, невозможно различить по форме и поэтому Pîø = 1 − Ф(0) = 0,5. Наиболее эффективно различимы сигналы, одинаковые по форме и противоположные по знаку, т.е. для них ks = −1. На рис. 3.10,а показаны результаты расчета по формуле (3.58). Зависимость Pîø = f [2Es  N0 ] при оптимальных методах приема сигналов называют кривыми потенциальной поме-
N0 ] при оптимальных методах приема сигналов называют кривыми потенциальной поме-
хоустойчивости.
à á
Рис. 3.10. Зависимость полной вероятности ошибки Pîø от коэффициента взаимной корреляции ks между детерминированными сигналами (а)
и кривые потенциальной помехоустойчивости (б) для АМ, ЧМ, ФМ
95
На рис. 3.10,б показаны эти кривые для трех видов модуляции: АМ с сигналами s1(t) = A0 cos(ωt + ϕ) è s0 (t) = 0; ЧМ с сигналами s1(t) = Acos(ω1t + ϕ) è s0 (t) = Acos(ω0t + ϕ), причем обычно
(ω1 − ω0 ) T >> 1 |
è ks = 0; ФМ с сигналами s1(t) = Acos(ωt) è |
s0(t) = −Acos(ωt), |
ò.å. ks = −1. Из графиков следует, что при задан- |
ной энергии элементарных сигналов наибольшую потенциальную помехоустойчивость имеют ФМ-сигналы.
3.6.2.Статистическиехарактеристикикачестваобнаружения
Вычислим показатели, определяющие качество работы оптимального обнаружителя. Выше было отмечено, что в РЛ-системах для задач обнаружения гипотеза H0 : y(t) = n(t). Выражения сигнала z на выходе корреляционного приемника для двух гипотез следуют из
(3.52) и (3.55). Условные ПРВ W (z H1 ) è W (z
H1 ) è W (z H0 ) также остаются гауссовыми. Их параметры (среднее значение и дисперсия) рассчи- тываются тем же способом, что и при выводе формулы (3.21). В итоге получаем:
H0 ) также остаются гауссовыми. Их параметры (среднее значение и дисперсия) рассчи- тываются тем же способом, что и при выводе формулы (3.21). В итоге получаем:
M[z H1 ] = |
2 |
Es |
N0 |
; |
Dz H1 |
= |
2 |
Es |
N0 |
; |
|
|
|
|
|
|
(3.59) |
||||||||
M[z H0 ] = 0; |
|
|
|
|
= 2Es |
|
|
|||||
|
|
Dz H |
0 |
N0 |
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
На рис. 3.11 показаны условные ПРВ; они имеют гауссову форму и отличаются, как и следует из (3.59), только положением.
В соответствии с критерием Неймана – Пирсона необходимо задать
ˆ |
H0 ), т.е. вероятность |
вероятность ложной (fals) тревоги F = P(H1 |
превышения порогового уровня zÏ случайной величиной z, когда на входе приемника имеется только шум:
|
|
|
|
|
|
|
∞ |
|
− |
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 (2Es |
N0 )dz |
|
|
|
|
|
zÏ |
|
|
||||||||
F |
= |
|
|
|
∫ |
e |
|
= |
1 |
− |
Ô |
|
. |
(3.60) |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2Es N0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2π zÏ |
|
|
|
|
|
|
|
|
|
|
|
2Es N0 |
|
|||||||||
Вероятность |
|
правильного |
обнаружения |
|
(detection) |
|||||||||||||||||||
|
ˆ |
H1 ) при этом оказывается равной: |
|
|
|
|
|
|
|
|
|
|||||||||||||
D = P(H1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
|
∞ − |
(z |
−q02 )2 |
|
|
|
z |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
Ï |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
D = |
|
|
|
|
∫ e |
|
2 q 0 |
dz = 1 − Ô |
|
|
− q0 |
, |
|
|
(3.61) |
|||||||
|
|
q |
|
2π |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
z |
|
|
|
|
|
|
|
q0 |
|
|
|
|
|
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

96
ãäå q0 = 2Es  N0 — отношение сигнала к шуму по напряжению на выходе коррелятора при t = T или на выходе СФ при t = t0.
N0 — отношение сигнала к шуму по напряжению на выходе коррелятора при t = T или на выходе СФ при t = t0.
На рис. 3.11 показаны площади, соответствующие величинам D
èF. Видно, что желание одновременного уменьшения F и увеличе- ния D является противоречивым. При заданном значении F из (3.60)
следует определить нормированный порог zÏ/q0 и затем согласно (3.61) вычислить вероятность правильного обнаружения D. Семейство
кривых D = f(q0) при F = const называют характеристиками обнаружения. Эти характеристики для оптимального обнаружителя сигнала с полностью известными параметрами следуют из (3.60), (3.61)
èпоказаны на рис. 3.12. Они позволяют для заданных значений F и D определить необходимое отношение сигнала к шуму.
Рис. 3.11. Нормальные ПРВ |
Рис. 3.12. Характеристики |
при наличии и отсутствии сигнала: |
обнаружения |
D — вероятность правильного |
детерминированного сигнала |
обнаружения; F — вероятность |
|
ложной тревоги |
|
Теория обнаружения утверждает, что никакой другой способ обработки, кроме оптимального, не может обеспечить лучшего сочетания параметров F, D, q0. В этом и есть сила и практическая польза результатов теории.
В разделе 3 показана важная роль согласованного фильтра (или коррелятора) при извлечении полезной информации о наличии сигнала известной формы в смеси с шумом. Повторим, что эффект улуч-
шения отношения сигнала к шуму на выходе СФ по сравнению с таковым на входе объясняется по существу когерентным (синфазным) сложением составляющих полезного сигнала и некогерен-
тным сумммированием шума. Например, в случае ФКМ-сигнала, со-
97
стоящего из М парциальных импульсов, комплексная амплитуда на-
|
& |
|
ïîñ- |
пряжения в максимуме на выходе когерентного сумматора SΣ |
|||
ле линии задержки с М-отводами (см. рис. 3.3–3.4) равна |
& |
|
& |
SΣ |
= MS1 |
||
( & — комплексная амплитуда парциального импульса). Соответствен-
S1
но мощность полезного сигнала PΣ = M 2 S12  2 . Поскольку шумы некогерентны и суммируются по мощности, то их средняя мощность в полосе ∆Fopt фильтра, согласованного с парциальным импульсом
2 . Поскольку шумы некогерентны и суммируются по мощности, то их средняя мощность в полосе ∆Fopt фильтра, согласованного с парциальным импульсом
длительностью ∆ = τè /M, равна Pn = M σn2 = MN0 ∆Fopt . |
Полоса |
|||||||||||
∆F |
≈ 1 2∆ , так как СФ имеет АЧХ вида |
sin x x 2 . Для отношения |
||||||||||
opt |
|
|
|
|
|
|
|
|
|
|
|
|
сигнала |
ê øóìó |
|
по мощности на |
выходе |
ÑÔ |
|
получим: |
|||||
q2 = |
P |
P = 2E |
s |
N |
0 |
, где полная энергия сигнала E |
s |
= τ |
è |
S2 2 . |
||
0 |
Σ |
n |
|
|
|
|
|
1 |
||||
На рис. 3.13 показаны осциллограммы процессов при согласованной фильтрации ФКМ-сигнала (7 позиционный код Баркера).
Длительность сигнала τè соответствует семи клеткам на экране. На рис. 3.13,а,б показан ВЧ-процесс (смесь сигнала и шума) на входе фильтра и огибающая на выходе фильтра при отношении уровня сигнала к среднеквадратичному значению шума примерно равном 10. Очевидно, что проблемы обнаружения такого сильного сигнала практически нет. Проблема обнаружения (различения) возникает, когда сигнал на входе СФ сравним по уровню с шумом и это видно на рис. 3.13,в,д. Положение существенно улучшается на выходе фильтра (рис. 3.13,г,е).
Следует обратить внимание на боковой всплеск слева от главного максимума на рис. 3.13,е. В данном случае он соответствует боковому лепестку функции неопределенности полезного сигнала (см. рис. 3.4). Однако в реальной РЛ-системе, когда число целей заведомо неизвестно, этот боковой максимум может принадлежать другому объекту, сигнал от которого более слабый. Это означает, в частности, что уровень боковых лепестков ФН сигнала имеет важное значение в плане достоверности получаемой в РТС информации. Он должен иметь вполне определенную величину, зависящую от динами- ческого диапазона полезных сигналов на входе.

98 |
99 |
3.6.3.Общие чертызадачсыщика и оптимального обнаружителя
Алгоритмы обнаружения и различения сигналов, полученные выше, по своей логической структуре «сходны» с процедурой, которую реализует детектив при «поиске-обнаружении» преступника (полезный сигнал) в большой толпе (шум) людей. Действительно, он заведомо изучает облик и повадки преступника — собирает всю априорную информацию о нем. В самой благоприятной (простой) ситуации он имеет его фотографию (опорный сигнал) и точно знает, где и когда (в каком кафе и в какое время), как правило, появляется «сигнал — преступник». Все действия (рассуждения) и принятие решения осуществляет мозг детектива (вычислительное устройство). Проблема в том, что реально всегда существует помеха: есть «люди — шум» и неизвестно точно, есть ли там преступник сегодня.
Задача обнаружения, конечно, будет намного сложнее, если информация о сигнале станет не такой полной. Радиосигнал может иметь неизвестное время прихода (и преступник тоже) или, например, неизвестную и случайную амплитуду и начальную фазу. Преступник также может изменить черты лица. Наконец, и шум может быть не белый и не гауссов — люди могут быть в кафе, на пляже, где они (и преступник тоже) … в темных очках. Что должен сделать сыщик, не нарушая закон, чтобы побудить посетителей снять очки, дабы повысить вероятность обнаружения? Оптимальный алгоритм обнаружения при этом окажется другим. В теории обнаружения получены мощные результаты для различных, встречающихся на практике, ситуаций.
Легко представить, что число обоснованно разнообразных задач обнаружения велико. Однако следует уяснить два очевидных обстоятельства: ставить задачу обнаружения (различения), ничего не зная о сигнале, не имеет смысла, и эффективность обнаружителя (разли- чителя) всегда будет выше, если он наиболее полно учитывает апри-
орную информацию об ожидаемом сигнале и шуме.
Читателю, который проявит глубокий интерес к задачам теории Рис. 3.13. Осциллограммы процессов при согласованной фильтрации обнаружения сигналов, можно рекомендовать для изучения [7, 9, 13].
ФКМ-сигнала в смеси с гауссовым шумом:
а, б — на входе фильтра отношение сигнала к шуму равно 10; в–е — отношение сигнала к шуму равно 1,5
