Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Основы СВЧ электроники.-1

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.28 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Добротности в резонаторе связаны уравнением (1.18).

Степень затягивания частоты оценивается соотношением (1.36)

F = 0, 417

. Коэффициент полезного действия резонатора связан с доброт-

Qвн

ностями (1.43)

h =

Qн

= 1-

Qн

. Внешняя добротность тогда может

Qвн

Q0 + Qвн

быть определена из уравнения

Qвн

= 0, 417

. Нагруженная добротность из

Fз

соотношения

Qн = h×Qвн = h×0, 417 ×

.Собственная добротность из уравнения

Fз

добротностей определяется

в виде Q0 =

Qн ×Qвн

Qн + Qвн

Рассчитаем требуемые по условию задачи величины

109

Qвн

= 0, 417

= 208, 5 » 208

0,5 ×107

Qн = 0, 9 × 208,5 = 187, 7 » 188

187, 7 × 208, 5

39135, 45

» 1880

-187, 7 + 208, 5

20,8

Qн

187, 7

= 1880

1- h

0,1

Задача №5 (Расчет тороидального резонатора)

Тороидальный медный резонатор используется в генераторном приборе СВЧ. Определить его резонансную частоту и предъявить требование к величине электронной проводимости, если размеры радиусов резонатора

R 2 =10 мм, R1 = 5 мм, высота резонатора 10 мм, размер зазора 1 мм. Резонатор связан петлей с коаксиальной линией имеющей волновое сопротивление 50Ом, отношение площади петли связи Sn к площади сечения резонатора Sr в плоскости входа петли в резонатор равно 0,08.

Решение Для возбуждения генератора необходимо выполнить условие баланса

активных проводимостей (баланс амплитуд), т.е.

Gэл + G0 + Gн £ 0 .

Откуда к активной проводимости электронного потока Gэл требование

имеет вид: -Gэл ³ G0 + Gн .

Следовательно, необходимо найти сумму проводимостей резонатора и нагрузки Gн , трансформированной к зазору. Коэффициент трансформации n проводимости нагрузки определяется соотношением

n = (1, 1 ¸ 1, 2 ) S n = 1, 1 5 × 0 , 0 8 = 0 , 0 9 2 . S r

Проводимость коаксиальной линии, являющейся нагрузкой [18], равна

m = -1.

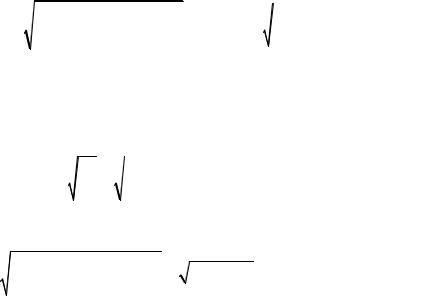
		1	n2 = 0, 02 ×(0, 092)	2	= 2 ×10−2 ×8,5 ×10−3 = 17 ×10−5 = 1, 7 ×10−4		1
Gн	=					,		.
		W
							Ом

Определим резонансную длину волны резонатора по формуле (1.22)

= pR1

4d h

×ln

= 3,14 ×0,5 ×

2 ×10

4 ×1 h

×ln 2

= 9,85 см.

5 d

Резонансную проводимость резонатора, используя формулу (1.27), найдем

h - d

R 2

−18 −1

= {

+ 2 ln

}

60L(см)

где Rs

= 0, 045

wmст

- поверхностное сопротивление.

2sст

L = μh ln

- эквивалентная индуктивность резонатора.

2p×3, 045 ×109 ×4p×10−7

=1, 42 ×102

20, 7 ×10−5

, Ом.

2 ×5, 9 ×107

Z =

4P ×10−7 ×10−2

ln 2 = 2 ×10−9

×0, 693 = 1,386 ×10−9 Гн;

1Гн= 109 см.

1, 42 ×10−2 9, 35

+ 2 ln 2 = 0,135 ×10−4

, См .

2 ×3,14

×1, 386

G0 + Gн = 1, 7 ×10−4 + 0,135 ×10−4 = 1,835 ×10−4 См

Откуда -Gэл > 1,835 ×10−4 См. . Для устойчивой работы генератора достаточно.

Задача №6. (Расчет спиральной замедляющей системы [11,13]) Рассчитать геометрию спиральной однозаходной замедляющей системы

ЛОВ для диапазона λср = 10 см . Лампа работает при ускоряющем напряжении,

равном 890 В. Номер пространственной гармоники Решение:

На рис.1.9. изображены схематично спиральная ЗС, геометрические параметры, которые необходимо рассчитать.

Известно ускоряющее напряжение, можно определить коэффициент замедления волны в спирали Kз, а затем выразить коэффициент замедления через геометрию.

	Kзам		=		C				(1.51)
	Kзам		=	Vфm					(1.51)
				Vфm
где C – скорость света;									Vфр – фазовая скорость p-ой гармоники.
C = λ × f , V	= λ		× f и V				=	ω	; C = ω .
C = λ × f , V	= λ	з	× f и V				=	βm	; C = ω .
фm		з				фm			k
					λ				k
	K зам		=		λ				(1.52)
	K зам		=		λз				(1.52)
					λз

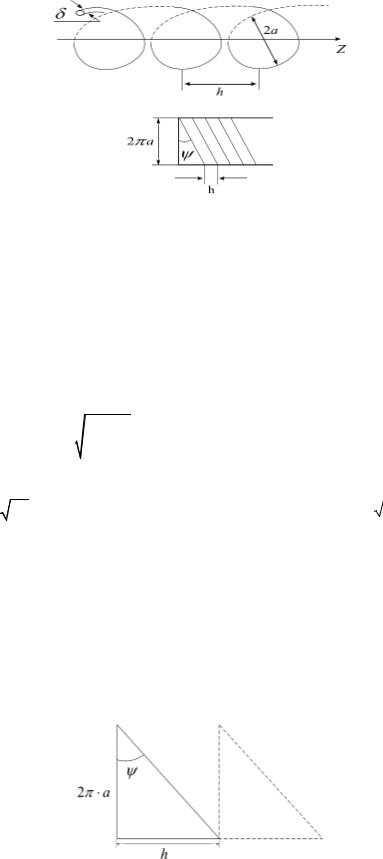
Kзам =	βm × a	(1.53)
	k × a

где a – радиус спирали, к- волновое число свободного пространства.

Рис.1.9. Спиральная замедляющая система.

ψ - угол навивки спирали; δ - диаметр провода; 2a - диаметр спирали; h - шаг спирали.

Фазовая скорость волны первой отрицательной пространственной гармоники должна быть примерно равна скорости электронного потока.

Vфm @ V0 .

V0 –

скорость электронов определятся из (1.2), фазовая скорость p-ой

гармоники равна V =

, тогда

фр

β p

β0

2π × p

×U0

(1.54)

2π × m

β0

Т.к.

505

, то коэффициент замедления (1.51) K зам =

505

= 17

Vфm

890

Определим угол намотки спирали ψ , используя соотношений (1.53)и

(1.54) .Здесь m = −1;

, т.к. для нулевой гармоники в области наших

2π × a

β0

частот дисперсия отсутствует. Тогда

Kз =

2π ×a

[1+

(-1)

]

(1.51,б)

Vф

a ×k

Из рис.1.10 запишем

2π × a

= ctgψ

(1.55)

Рис.1.10 Развертка спирали на плоскость.


Значение ctgψ берется большим,	при ψ → 0 ,				т.к. при этом снижается
U раб ; увеличивается N - число длин волн вдоль оси спирали ,уменьшается ра-
					1
бочая длинна лампы L. Для однозаходной спирали					[15] величина 2 P				P 6 .
								a × K
Это видно из равенства (1.55), т.к. при	1	= 2 ;	C	=		2π × a	, а это соотношение
	a × k
		Vф				h

близкое или равное значению нулевой гармоники, которая при этом возбуждается быстрее, чем первая отрицательная гармоника.

При

P 5 ¸ 6

величина

сопротивления

связи уменьшается, а

это

a × k

уменьшает выходную мощность P.

Задаем

= 3 , тогда радиус спирали:

a =

= 0.53

см

6π

18.8

= ctgψ (-2)

(1.56)

Vф(−1)

Минус (-) – показывает,

что обратная гармоника, но при расчетах

его

можно опустить.

= ctgψ = 8.5 ,

ψ = 60 40',

a = 0.53 см .

Найдем шаг спирали h из (7) и оценим диаметр проволоки. Т.к.

2πa/h=8,5,

то

h =

6.28 × 0.53

= 0.39 cм .

8.5

При выполнении 0.3 £ δ £ 0.5 минимум потерь в проводниках системы.

Берем δ = 0.4

δ = 0.4 × 0.39 = 0.156 cм .

Оценим сопротивление связи спирали при r = a , воспользовавшись фор-

мулой [15]

Rсв (a) =

16.7

(1.57)

(

- 0.923)2 a × K

Это сопротивление связи определено на самой спирали, но т.к. пучок

проходит на некотором расстоянии от спирали,			равном	b - a	, то следует в
проходит на некотором расстоянии от спирали,			равном	b - a	, то следует в
формулу (1.57) внести поправку, в виде:	J12 (γ b)
Rсв (b) = Rсв (a)	J12 (γ b)	,
Rсв (b) = Rсв (a)	J12 (γ a)	,

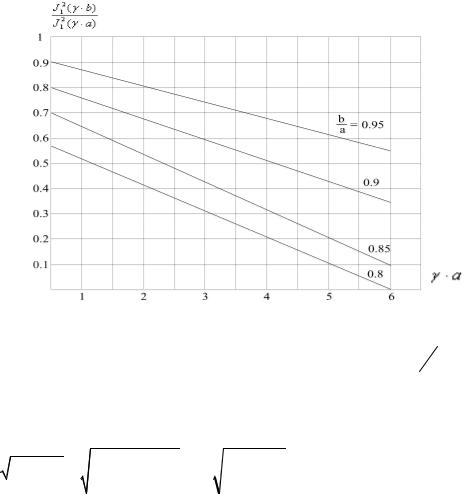
Рис.1.11. Поправочные коэффициенты для вычисления действующего значения волнового сопротивления при различных значениях b a .

где

J0 – функция Бесселя; γ

- фазовая постоянная распространения волн в

направлении радиуса. Смысл тот же, как для гребенки у величин ξ1

и h1 .

= ω

» ω ×

6.28 ×3×109

γ =

(

)2 - (ω )2

(

)2 -1

β 2 - K 2

= 5.6

C V

5.95 ×105 × 29

фm

По графику рис.1.11 определим поправочный коэффициент для

= 0.9 .

J12 (γ b)

Rсв

r =b =

16.7

× 3

× 0.38 = 5.6 Ом

=0.9 = 0.38 ,

J12 (γ a)

(3 - 0.923)2

U 2

Найдем волновое сопротивление спирали, пользуясь формулой W (U ) =

по напряжению, W ( J ) =

по току.

J 2

376 × β0 × J 02 (γ a)

π × K ×γ × a × F (γ a)

где

J0 – функция Бесселя нулевого порядка.

Или более простая формула волнового сопротивления спирали в цилин-

дре, что практически всегда выполняется

W = 60K зам J 0 (γ a)N 0 (γ a) ,

где N0 – функция Неймана нулевого порядка. Для нашего случая имеем:

W = 60 ×17 × 0.027 × 0.34 = 9.3 Ом

Как видно волновое сопротивление не равно сопротивлению связи. Вывод: Определена геометрия, параметры работы в ЛОВ на m = -1, Rсв и

W спирали для замедляющей системы.

2a	h	δ	ψ	Rсв	b	W	λ	U0
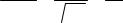
2a	h	δ	ψ	Rсв	b	W	λ	U0

1.06 см	0.39 см	0.156	60 40'	5.6 Ом		9.3 Ом	10 см	890 В
		см

Задача №7 (Рабочий диапазон замедляющей системы встречные штыри) В каком диапазоне длин волн может работать замедляющая система типа встречные штыри (рис. 1.12), если рабочее ускоряющее напряжение изме-

няется в пределах 324 B ÷1600 B . Замедляющая система используется в ЛОВО на m = −1, длина штыря составляет b=20 мм, период h =2 мм.

Решение:

Для решения этой задачи необходимо воспользоваться условием фазово-

го синхронизма.			Vф @ V0 =		C
го синхронизма.			Vф @ V0 =		K зам
					K зам
Для нулевой гармоники это условие можно записать в другом виде
	h + b	=	C	= K зам0	(1.58)
		=		= K зам0	(1.58)
	h		Vф0

Для m-ой гармоники фазовое условие можно получить из соотношения для постоянной βm

βm	= β0	+	2π × m	(1.59)
			2h

Здесь

β0 =

2π × f

2π

Vф0

2π × f

2π × m

×λ ,

Vфm

Vф0

+ λ ×m

(1.60)

Vфm

Vф0

Из (1.58) и (1.60) имеем

h + b

+ λ × m =

h + b

Vф1

Но, учитывая отрицательный знак Vф(−1)

и для ЛОВ на -1-ой гармоники

имеем:

= -(

h + b

) .

(1.61)

Vф(−1)

Используя (1.61) найдем выражение в общем виде для определения диа-

пазона длин волн. Для расчетов следует брать

, тогда

Vф(−1)

С= 505 = λ - λ + b .

Vф(−1) U 0 2h h

Т.к. два напряжения заданы, то определяем большую и малую длину волны

(	505			+	λ + b ) × 2h = λ ;			(	505	+	20 + 2	) × 0.2 × 2 = λ ;

		U 0			h			1600		2		1

		(	505		+	20 + 2	) × 0.2 × 2 = λ2		(12.6 + 11)0.4 = 9.44 см ; (28 + 11)0.4 = 15.6 см;


324					2

Ответ: 9.44 ≤ диапазонλ ≤ 15.6

Задача №8. (Расчет геометрии ЗС типа встречные штыри ) Решение проводится в общем виде для любой гармоники [14].

Рис.1.12. Замедляющая система типа встречные - штыри.

Размер δ (рис.1.13) не влияет на дисперсионные свойства замедляющей системы. Поэтому размером δ можно при расчете геометрии задаться согласно технологии. Точно также поступают и с размерами и m, b, a, W.

Рис.1.13.Зависимость коэффициента замедления от длины волны при разных размерах δ.

Считая, что волна движется по известному пути между штырями, со

скоростью света С, имеем:

b + h

. Т.к.

βm = β0 +

2π × m

Vф0

2π ×C

2π × f

2π ×C

β0 =

получаем

βm =

или

Vф0

λ ×Vфm

λ ×Vф0

2π ×C

2π × m

C C m ×λ

b + h

m ×λ

λ ×V

фm

ф0

фm

ф0

фm

здесь m = 0, ±1, ± 2...

U min

λmin

- λmax

и U max .Таким образом из

Это выражение описывает достаточно хорошо для практических целей дисперсионные характеристики однорядных и двухрядных замедляющих систем типа встречные штыри.

При изменении b кривые смещаются параллельно себе.

Рис.1.14.Поведение коэффициента замедления в диапазоне длин волн для разных значений b и h.

Таким образом, варьируя h и b, можно получить желаемое замедление при данной длине волны λ и наоборот. От остальных параметров характери-

стики почти не зависят.

Выбор оптимальных размеров замедляющих систем.

Пусть задан диапазон и диапазон

формулы (3.4) можно определить m, h. Задается номер гармоники, пусть m = −1. Кривая электронной настройки дает λmin -U max и λmax -U min .

= - h + b + λmin

= 505

5.95 ×105 ×

Umax

h + b

λmax

505

= -

5.95 ×105 ×

Umin

λmax - λmin =

505

U min

U max

2h =

λmax - λmin

505

U min

U max

где h – период замедляющей системы типа встречные штыри.

Из

λmax

- 2

b + h

2h ×505

2h × Umin

λmax − λmin

2b = λmax

- 2h - 2h ×

505

= λmax - 2h ×(1-

505

) = λmax

(1-

505

) =

505

Umin

Umax

λmax

× (

505

) - λmax +

505

× λmax + λmin - λmax

505

U min

U max

U min

505

U min

U max

λmin	× (1 +	505		) - λmax × (1 +				505	)

		U min					U max			= 2b
	505				-	505				= 2b
	505					505

			U min			U max

Сопротивление связи Rсв увеличивается при уменьшении расстояния между рядами штырей системы типа встречные штыри- a ( рис.1.15), а дисперсия от a не зависит. Исходя из этого, величину a нужно выбирать минимальной.

Рис.1.15 Зависимость сопротивления связи от расстояния между рядами штырей a в замедляющей системе.

Однако, если a выбирается минимальной, то при заданной величине тока J прибора и плотности тока эмиссии jk , то высота электронного потока b

должна быть определенной, согласно известному соотношению J £ jk .

Рис.1.16. Влияние на сопротивление связи размеров p, b.

Хотя, сопротивление связи Rсв увеличивается с ростом h и уменьшением р, свойства дисперсионные остаются неизменными. Кажется можно увеличивать h и уменьшать р, но при этом ухудшаются тепловые и механические параметры замедляющих систем. Поэтому h и р выбирают из требований механической прочности конструкции ЗС прибора и ее теплового режима,

Обычно p @ b @ h .

Из конструктивных и технологических соображений выбирают δ и W .

δ = 0.5 ÷1 мм W F h

Длина замедляющих систем определяется параметром усиления, который зависит от длины волны в ЗС, от числа N замедленных длин волн λз, уложившихся вдоль неё (см. раздел 3, далее)

K ус = f (N ×λ) .

1.3. Задачи для самостоятельного решения

1.3.1. Для плоского кремниевого диода определить углы пролета носителей заряда в диффузионном и дрейфовом приближениях. Длина промежутка d =1,5мкм, рабочая частота f = 1,5 ГГц. Постоянное напряжение на промежутке U0 = 10,2 В. Как изменится режим работы, если U0 увеличить до 30В?

Ответ: θдр=0,141 рад. ; θдиф=2,1·10-6 рад.

1.3.2.Разность потенциалов между плоскими электродами U=500 В.

Электрон начал движение в электрическом поле от одного из электродов, имея нулевую скорость, и получил ускорение 4·1015 м/с2 . Определите расстояние d между электродами.

Ответ: 2,2 см.

1.3.3.Определить длину пролетного пространства ЛПД, предназначенного для работы на частоте f = 5ГГц. Материал – кремний. Движение элек-

тронов происходит с дрейфовой насыщенной скоростью. Максимальный угол пролета следует взять величиной π радиан.

Ответ: lдр = 10-5 м

1.3.4. В плоский зазор резонатора длиной 10 мкм поступает модулированный по плотности поток электронов, при этом iкон = I0 + Im sin ωt . Во сколько раз амплитуда тока, наведенного во внешней цепи, меньше величины Im , если рабочая частота прибора 3,31 ГГц? Зазор представляет промежуток полупроводникового материала GaAs, режим движения носителей в котором идет с насыщенной дрейфовой скоростью. Какую величину зазора d следует обеспечить для сохранения той же амплитуды наведенного тока, ес-

ли повысить рабочую частоту до 11,58 ГГц?

Ответ: I=0,83·I0 ; d увеличить в 3,5 раза.

1.3.5. Определить граничную частоту(qгр » p) , при которой еще воз-

можно статическое описание работы прибора, если плоский германиевый диод имеет размер промежутка d = 10 мкм, питающее напряжение 5В. Расчеты провести для режимов дрейфа, диффузии и баллистического движения.

Ответ: f.др.= 3·109 Гц; fбалл..=6,65·107 Гц; fгр.диф.=9,76·107 Гц.

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20236.17 Mб33Основы радиотехники..pdf
#
05.02.20233.04 Mб38Основы радиоэлектроники и связи.-1.pdf
#
05.02.2023459.2 Кб12Основы радиоэлектроники и связи..pdf
#
05.02.2023258.74 Кб6Основы разработки коммерческого программного обеспечения.-1.pdf
#
05.02.2023953.07 Кб10Основы разработки коммерческого программного обеспечения..pdf
#
05.02.20231.28 Mб35Основы СВЧ электроники.-1.pdf
#
05.02.20231.24 Mб21Основы СВЧ электроники..pdf
#
05.02.2023274.08 Кб12Основы системного анализа и системного подхода..pdf
#
05.02.20231.71 Mб10Основы создания графического программного интерфейса в среде Lazarus..pdf
#
05.02.2023517.17 Кб1Основы социального благополучия личности и общества.-1.pdf
#
05.02.2023236.41 Кб3Основы социального благополучия личности и общества.-2.pdf