Мультиплексорное и усилительное оборудование многоволновых оптических систем передачи.-2

80

Поскольку подвижность молекул образующегося полимера значительно меньше подвижности молекул мономера, красителя и донора, то диффузия полимера проявляется на гораздо больших временных интервалах

Показатель преломления полимера больше показателя преломления исходного мономера. Таким образом, модуляция показателя преломления Δn в ФПМ возникает как следствие модуляции концентрации полимера. Скорость изменения концентрации мономера со временем записи равна:

где I(r) — интенсивность светового излучения в точке с радиус-векто- ром r; Dm — коэффициент диффузии мономера; — коэффициент поглощения красителя; K — концентрация красителя; — параметр реакции фотоинициирования.

Изменение во времени М в некоторой точке приводит за счет процесса полимеризации к изменению во времени плотности полимерных молекул в этой точке. За счет процессов диффузии мономера происходит также вытеснение инертной компоненты. Все эти процессы в соответствии с соотношением Лоренц — Лорентца ведут к изменению показателя преломления n:

где M0 — начальная концентрация мономера.

Система уравнений (2.33) и (2.34) является базовой для описания процесса записи голограмм в фотополимерном материале.

Аналитическое описание динамики записи одиночных голограмм.

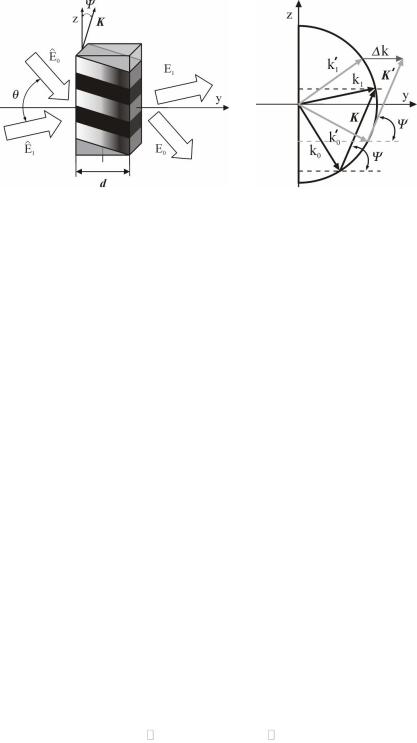
Схема записи голограммы в полимерной среде изображена на рис. 2.33. Оптическое поле представляется суммой двух волн с векторными амплитудами E0, E1 и волновыми векторами k0, k1

где A0, A1 медленно меняющиеся по r и t амплитуды волн; e0, e1 — векторы поляризации этих волн.

Падающие волны интерферируют внутри полимерного слоя и формируют интерференционную картину. Предположим, что А0 = А1, и что среда обладает коэффициентом затухания , так что интерференционная картина светового поля имеет вид:

где I0(r) A0 2+ A1 2 — пространственное распределение интенсивности, K k0 – k1 — вектор решетки.

81

а б Рис. 2.33 — Пространственная геометрия (а) и векторная диаграмма (б)

нестационарного взаимодействия световых волн

сголографической решеткой в ФПМ для несимметричной модели записи

Вкинетических уравнениях записи (2.33), (2.34) в общем случае проис-

ходит изменение амплитуд записывающих световых волн A0, A1, обусловленное эффектами самодифракциии на формируемой решетке в области ФМП. Данный процесс описывается системой уравнений связанных волн

[31]

где n1(y,t) — амплитуда решетки; y x/d (r х0)/d; х0 — нормаль к границе

среды; (k0 – k1 + K) х0d; Gj d/(2ccos j); j — углы между осью y и векторами kj внутри полимерного слоя толщиной d.

Совокупность уравнений (2.33), (2.34) и (2.37) образует замкнутую систему, описывающую процесс записи голограмм в ФПМ в соответствии с распределением интенсивности света (2.36).

Учитывая, что в процессе последовательной записи наложенных голограмм в ФПМ дифракционная эффективность каждой из них является невысокой, возмущением полей (2.35) вследствие эффектов самодифракции волн E0, E1 на записываемых решетках будем пренебрегать. Это позволяет считать амплитуды A0, A1 в (2.36) постоянными и решения (2.33), (2.34) искать в виде суммы нулевых и первых гармоник

M t,r M0 t, y M1 t, y cos(K r) ; n t,r n0 t, y n1 t, y cos(K1r) .

Допуская, что М1(t,у) M0(t,у) и n1(t,у) n0(t,у), можно пренебречь влиянием первой гармоники на нулевую и, используя начальные условия

Решение (2.41) записано как функция от пространственной и временной координаты. Отсюда сразу следует, что в процессе записи, во-первых, амплитудный профиль записываемой решетки является неоднородным, во-вторых, трансформируется во времени, и в-третьих, кинетика изменения амплитуды решетки в каждой пространственной точке является различной и определяется вкладами в амплитуду голографической решетки процессов полимеризации и вытеснения инертной компоненты за счет диффузии мономера, которые пропорциональны np и ni.

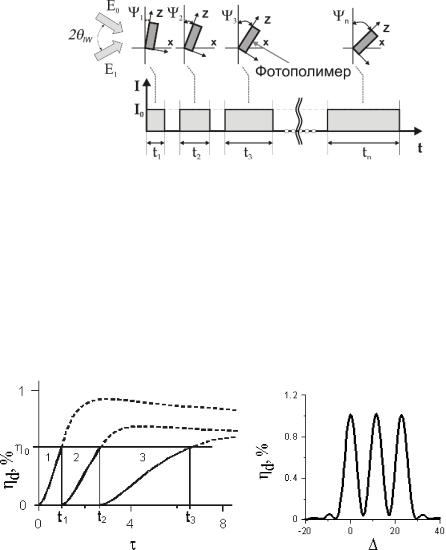
Аналитическое описание и алгоритм процесса записи наложенных голограмм. Принцип записи голографических НДР схематически показан на рис. 2.34. Каждая голограмма записывается под своим углом i, с одинаковым углом схождения записывающих лазерных пучков IW в течение определенного времени ti. При этом в ФПМ из-за процессов радикальной полимеризации формируется фазовая голографическая решетка. Типовые

83

характеристики динамики записи таких решеток, т.е. зависимости дифракционной эффективности от времени записи (экспозиции), для трех первых НДР представлены на рис. 2.35.

Моделирование механизма последовательной записи НДР в ФПМ состоит в следующем.

Рис. 2.34 — Схема последовательной записи НДР в ФПМ

Записывается первая голограмма (кривая 1, рис. 2.35,а) под углом 1 (угол между нормалью к полимеру и биссектрисой угла схождения записывающих пучков) и с начальной концентрацией мономера Mn1 Mn0, где Mn0 — начальная концентрация мономера до процесса записи. По мере записи решетки мономер расходуется за счет реакции полимеризации. При достижении за время экспозиции t1 заданной дифракционной эффективности решетки η0 запись голограммы прекращается (рис. 2.35,а) и определяется оставшаяся концентрация мономера Mn2 < Mn1. Отметим, что на рис. 2.35,а, пунктирной линией обозначена динамика записи дифракционной решетки, если бы запись голограммы продолжалась далее.

а б Рис. 2.35 — Динамика дифракционной эффективности (а)

и зависимость нормированной дифракционной эффективности от расстройки Брегга (б) для трех последовательно записываемых НДР

84

Записывается вторая голограмма (кривая 2, рис. 2.35,а) под углом 2 (рис. 2.34), но уже с начальной концентрацией мономера Mn2. При достижении значения η0 через промежуток времени t2 запись голограммы прекращается и определяется оставшаяся концентрация мономера Mn3 < Mn2. Далее этот процесс повторяется столько раз, сколько голограмм необходимо записать. Отметим, что время экспозиции с ростом порядкового номера записываемой голограммы и при условии равных дифракционных эффективностей увеличивается. Это связано с изменением динамики записи голограмм (рис. 2.35,а). Вследствие истощения концентрации мономера необходимо больше энергии для достижения той же дифракционной эффективности, как у предыдущих голограмм.

На основе найденных времен записи рассчитывается зависимость интенсивности дифрагированного пучка от относительной расстройки Брегга либо от угла падения считывающего голограмму луча, или от длинны оптической волны. В последних двух случаях получаем угловой или частотный спектр для устройства селекции длин волн на основе НДР, записанных в ФПМ. На основе этих спектров (аппаратных функций) определяются переходные помехи и соответствие их поставленным требованиям. На рис. 2.35,б приведена зависимость нормированной дифракционной эффективности от расстройки Брегга для трех записанных НДР при следующих параметрах модели: 1 Нп; δnp 10 –2; δni 10 –2; d 20 мкм; n 1,45; IW 20º; Ψ1 0º; Ψ2 5º; Ψ3 10º. Все три голограммы записаны при условии равенства их дифракционных эффективностей (η0 1 %)

Математическую модель для записи одиночной голограммы можно модифицировать на случай последовательной записи нескольких наложенных голограмм в ФПМ.

Введем в решения (2.40) и (2.41) индекс i — номер голограммы, и перепишем их с учетом истощения мономера для каждой последующей записанной решетки. Выражение для амплитуды первой гармоники концентрации мономера для i-й голограммы запишется:

Mni — начальная концентрация мономера на момент записи i-й голограммы, Tpi — время полимеризации на момент записи i-й голограммы.

85

Амплитуда первой гармоники показателя преломления n1i(t,y):

Выражение (2.46) совместно с первым уравнением (2.37) составляет основу для определения дифракционной эффективности i-й НДР

где G1 d/ cos( i), i — угол cчитывания i-й голограммы в фотополимере и соответственно коэффициента передачи i-го канала демультиплексора,:

оптической волны – i и угла считывания – i ( /2n cos i)

относительно их значений, удовлетворяющих условию Брэгга sin I 2 i/n . Таким образом, выражения (2.46) и (2.48) являются математической

основой для компьютерного моделирования аппаратной функция WDMдемультиплексора на основе наложенных голограмм в ФПМ.

2.4.3. Расчет основных оценочных характеристик

Для того чтобы построить демультиплексор на основе наложенных решеток в фотополимерном материале, необходимо рассчитать параметры записи этих решеток в соответствии с заданными требованиями к разрабатываемому демультиплексору.

При использовании дифракционной решетки в качестве фильтра для заданной длинны оптической волны λi важно определить угол di, под которым будет дифрагировать луч. Угол определяется из условия Брэгга:

где çàï 2sin çàï — период решетки. Для последовательной записи голограмм период решеток одинаков, т.к. угол записи всех голограмм

86

постоянен, а изменяется только наклон ФПМ на угол ΔΨ. Учитывая это, перепишем (2.49) в виде

Величина ΔΨ определяется при заданной величине канального интервала fk из условия обеспечения требуемого уровня переходных помех между каналами. Дифференцируя (2.50), найдем изменение di

где k fkc/f2. Для обеспечения углового разрешения дифракционных максимумов смежных каналов необходимо выполнение условий

где /D — угловая расходимость падающего светового пучка с апертурой D; /d — угловая селективность голографической решетки. Угловая селективность определяет такой угловой разнос дифрагированных лучей, при котором переходные помехи будут удовлетворять поставленным требованиям.

Следовательно оценочное значение ΔΨ найдется как

Максимальную достижимую дифракционную эффективность голографических решеток можно оценить по формуле

где n — число наложенных решеток в ФПМ.

Для заданной толщины решетки d и оценки (2.53) из выражения для дифракционной эффективности

можно определить требуемую амплитуду решетки n1i, и соответственно необходимое время ее формирования в процессе записи.

Относительную ширину полосы пропускания каждого канала можно оценить по формуле

i d ctg i .

2.5.Мультиплексоры на основе AWG

На сегодняшний день существуют различные устройства для мультиплексирования/демультиплексирования оптического потока, у каждого из которых есть свои достоинства и недостатки. Одним из приоритетов является

87

возможность создания WDM/DWDM-устройств с применением интегральнооптической технологии [3,27].

Интегральная оптика успешно применяется для создания решеток на основе массива планарных волноводов различной длины между двумя пла-

нарными линзами смесителями AWG (Arrayed Waveguide Gratings).

Решетки на основе массива волноводов AWG используются для того, чтобы перераспределять сигналы различных длин волн (каналы) между двумя наборами волокон или выделять (демультиплексировать) отдельные каналы составного сигнала в отдельные волокна. Эта технология сейчас становится основной для производителей мультиплексоров и демультиплексоров систем DWDM. Благодаря легко масштабируемой структуре, она может широко применяться в системах с сотнями каналов [27-29].

2.5.1. Принципы действия и структура мультиплексора

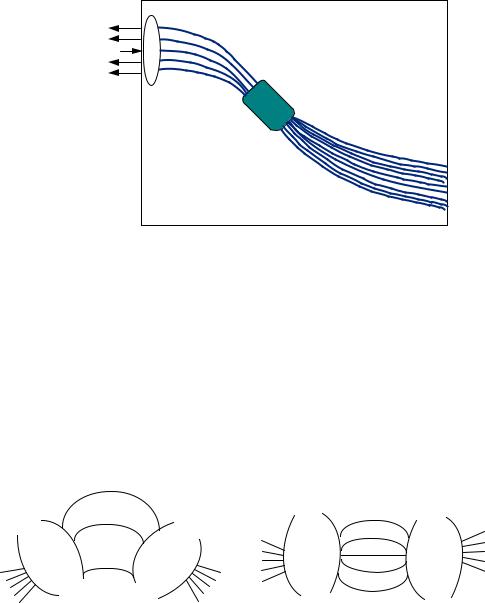
Устройство работает следующим образом. Если на вход планарной структуры подсоединить одномодовый световод и подавать по нему оптические сигналы с несколькими спектральными составляющими (на длинах волн λ1, λ2, λ3, … λn) в магистральный канал, то в первом фокусирующем элементе, выполняющем роль коллиматора, свет равномерно разделится и будет распространяться по канальным волноводам с разными длинами пробега, отличающимися постоянным интервалом. За счет материальной и волноводной дисперсии разные длины волн достигнут второго фокусирующего элемента с разными фазами. В зависимости от фаз световые пучки разных спектральных составляющих, выходящие из этого фокусирующего элемента, будут интерферировать и создавать равномерное угловое спектральное распределение, направляя различные спектральные составляющие в разные выходные каналы. К выходным каналам на торцевом конце планарного устройства может быть подсоединена линейка фотодиодов или линейка со встроенными стандартными одномодовыми волокнами для транспортировки оптических сигналов на различных длинах волн к оптоэлектронным блокам. Особенностью рассмотренной волноводной структуры является ее обратимость. Она может использоваться в качестве как мультиплексора так и демультиплексора [27].

Одной из конфигураций AWG является планарный оптический многопортовый разветвитель в форме таблетки с портом входа λ 0 и группой вы-

ходных портов 00 , 10 , , 0n , расположенной симметрично относительно 0 на периферии волновода слева, и группой внутренних выходных портовi0 , 1i , , in , расположенной симметрично группе выходных портов на периферии справа (рис. 2.36).

88

Порты ввода/вывода

λ1, λ2, λ3, λ4

λ3 λ4

Ввод

Дифракционная структура на основе массива волноводов

Рис. 2.36 — Многопортовый разветвитель

Внутренние выходные порты соединены через массив световодов с плоским отражающим зеркалом. Входной поток λ0 ∑ λi (i 1,2, ..., n) подается в оптический волновод и распределяется по всем внутренним портам, откуда он распространяется по массиву световодов (с разным фазовым запаздыванием) до зеркала, отражается и подается со стороны внутренних выходных портов в тот же волновод, где происходит интерференция входной и отраженных волн [29].

Еще одной конфигурацией планарных дисперсионных устройств,

является устройство с волноводами массива одинаковой длины, но с участками различных замедлений.

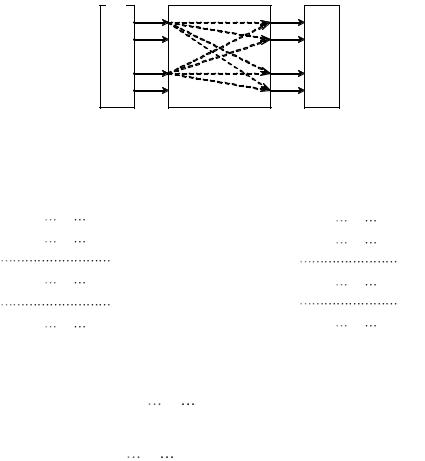
Существует еще одна модификация AWG, называемая Cross Array Waveguide (XWG) или Crossing Focal Points Waveguide (XFP-WG) (рис. 2.37).

Ее отличие заключается в том, что у AWG приращение длины ∆l между соседними волноводами начинается с нижнего волновода, который имеет наименьшую длину, тогда как у XWG наименьшую длину имеет средний волновод массива, а приращение длины ∆l происходит в обе стороны от него,