
Моделирование работы мультикоординатных систем движения.-1
.pdf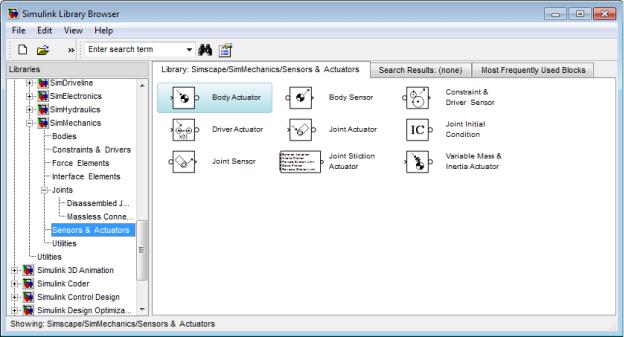
РазделSensors &Actuators
Раздел Sensors&Actuators(Датчики и приводы) (рис. 16) включает блоки Sensors, которые служат для измерения относительных движений тел, и блоки Actuators, задающие относительные движения.
Как ранее было отмечено, блоки типа Joint(Сочленения) могут быть снабжены дополнительными портами для подсоединения к ним блоков Actuatorи Sensor. Аналогичная операция возможна и по отношению к блокам
Body, Driverи Constraint.
Рис. 16. Блоки раздела Sensors&Actuators
Особенность блоков Actuatorи Sensorсостоит в том, что они являются связующимимежду механическими блоками библиотеки SimMechanicsи обычными S-блоками.Это позволяет использовать возможности библиотеки Simulinkдля формирования сигналов, их преобразования и перевода получаемых результатов в рабочеепространство Simulink.
Блоки возбудителей (Actuator) и измерителей (Sensor) относительного движенияразделены на три группы.
-BodyActuator(Возбудитель движения тела) и BodySensor(Измеритель движения тела) - предназначены для подсоединения к блокам Body; задают или измеряют абсолютное движение жестко связанной с телом системы координат,к которой они подсоединены.
-JointActuator(Возбудитель движения сочленения) и JointSensor(Измерительдвижения сочленения) - предназначены для подсоединения к блокам Joint;задают или измеряют относительное движение примитива, указанного в окненастройки.
21
-DriverActuator(Возбудитель нестационарной связи) и Driver&ConstraintSensor(Измеритель движения связи) предназначены для подсоединения к блокамDriverили Constraint; задают или измеряют относительное движение связи,с которой они соединены.
Вначале остановимся на особенностях использования блоков
JointActuatorи Joint
Sensor.На рис. 17 и 18 приведены окна настройки блоков. Рассмотрев этирисунки, можно сделать следующие выводы.
-С помощью блока JointActuatorможно в общем случае задать (как функциювремени) либо силовое взаимодействие между элементами примитива, имякоторого указывается в верхнем поле ввода, либо относительное движениеэлементов этого примитива. Установка вида возбуждения осуществляется путем активизации соответствующего переключателя - GeneralizedForces(Обобщенные силы) или Motion(Движение).
-Относительное движение частей примитива задается в виде векторного сигнала из трех элементов, первый из которых определяет относительное перемещение, второй относительную скорость, а третий относительное ускорение частей указанного элементарного сочленения.
-Блок JointSensorпозволяет в общем случае измерить следующие характеристики относительного движения частей примитива, имя которого устанавливается в верхнем поле ввода окна настройки блока:
• Angle(Угол) — угол поворота выходной части примитива (Follower) относительно его части, соединенной со входом (Base);
• Angularvelocity(Угловая скорость) - относительная угловая скорость;
• Angularacceleration(Угловое ускорение) - относительное угловое ускорение;
• Computedtorque(Вычисленный момент) — полный момент сил, вызывающий относительное угловое ускорение;
• Позиция — перемещение выходной части примитива (Follower) относительно его части, соединенной со входом (Base);
• Velocity(Скорость) относительная скорость;
• Acceleration(Ускорение) - относительное ускорение;
• Computedforce(Вычисленная сила) - полная сила, вызывающая относительное ускорение;
• Quaternion(Кватернион) - вектор из четырех элементов, характеризующийтекущее относительное угловое положение частей примитива;
• Quaternion, derivative(Производная от кватерниона по времени) - векториз четырех элементов, являющихся производными по времени от соответствующих элементов кватерниона относительного поворота;
• Quaternion, secondderivative(Вторая производная от кватерниона по времени) — вектор из четырех элементов, являющихся вторыми производнымипо времени от соответствующих элементов кватерниона относительногоповорота;
22
3. ПРИМЕРЫ СОЗДАНИЯ МОДЕЛЕЙ МАНИПУЛЯТОРОВ
Как правило, моделирование объектов, помимо чисто научных целей может иметь и прикладное значение. Для проектирования и анализа механических систем (например, различных кинематических цепей) давно разработан специальный физико-математический аппарат.
SimMechanics - пакет расширения системы Simulink для физического моделирования. Его цель - техническое проектирование и моделирование механических систем (в рамках законов теоретической механики). SimMechanics позволяет моделировать поступательное и вращательное движения в трех плоскостях. SimMechanics содержит набор инструментов для задания параметров звеньев (масса, моменты инерции, геометрические параметры), кинематических ограничений, локальных систем координат, способов задания и измерения движений.
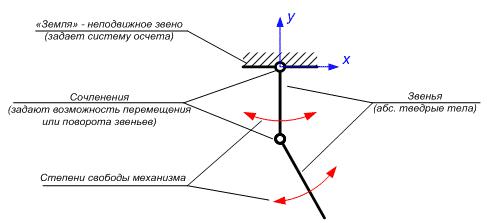
SimMechanics позволяет создавать модели механических систем подобно другим Simulink-моделям в виде блок-схем. Встроенные дополнительные инструменты визуализации Simulink позволяют получить упрощенные изображения трехмерных механизмов как в статике, так и в динамике. Любой механизм можно представить в виде совокупности звеньев и сопряжений. Например, звухзвенный физический маятник (см. рис. 1) представляет собой последовательное соединение следующих элементов:
-неподвижного звена (земли);
-шарнирного соединения (задающего 1-му звену одну степень свободы поворот вокруг оси z);
-первого звена (звено представляется как абсолютное твердое тело);
-шарнирного соединения между 1-ым и 2-ым звеньями (ограничивает степени свободы 2-го звена, оставляя также только поворот в плоскости xy);
-второго звена.
Рис. Модель двухзвенного физического маятника
23
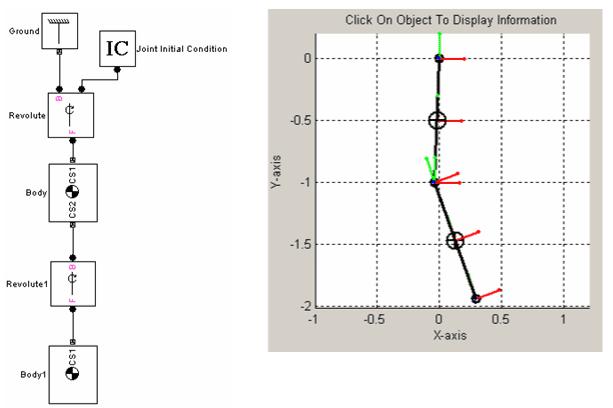
Simulink-модель такого механизма строится в аналогичной последовательности (см. рис. 2). Исходным элементом модели является звено Ground - земля. К нему присоединен элемент - Revolute (т.е. сопряжение, позволяющее следующему звену лишь поворачиваться вокруг указанной оси - z). Далее следует непосредственно звено физического маятника Body. В качестве параметров этого звена необходимо указать массу тела, моменты инерции относительно главных центральных осей симметрии, а также координаты верхнего, нижнего конца звена и его центра масс. При этом координаты можно задавать как в глобальной системе координат (ГСК), так и в локальной системе координат (ЛСК) звена.
Аналогично, к первому звену посредством шарнирного соединения Revolute 1 присоединяется второе звено Body 1.
Чтобы звенья спроектированного механизма начали движение необходимо либо добавить вынуждающую силу, либо задать начальные условия (например, начальное отклонение или сообщить начальную скорость). Для реализации последних используется блок InitialCondition.
а) |
б) |
Рис. Simulink-модель двухзвенного физического маятника (а) и моделью имитации движения (б)
На модели имитации отображаются звенья, колеблющиеся по законам классической механики (физики твердого тела). Там же отображаются ло-
24
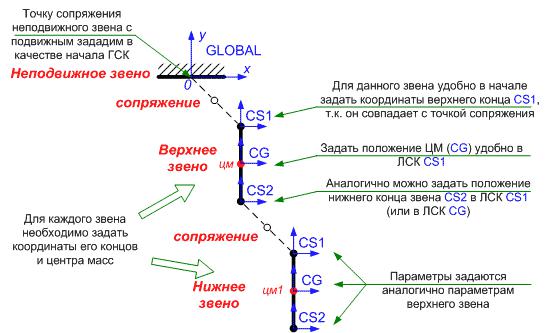
кальные системы координат (ЛСК) звеньев. Вопрос о выборе той или иной системы координат (СК) является очень важным. Правильный выбор СК значительно облегчает моделирование механизма и интерпретацию результатов.
При моделировании данного механизма использовались следующие СК
(рис. 3).
Неподвижная глобальная система координат ГСК Global находится в точке сопряжения неподвижного звена с верхним звеном (коленом маятника)2. Задавать координаты точек верхнего звена маятника можно различными способами, в том числе, просто перечислив их значения в ГСК. Однако это не всегда удобно.
Верхний конец первого звена сопрягается с неподвижным звеном, и поэтому его координаты совпадают с началом ГСК. Его координаты действительно легко задать как Global [0, 0, 0]. Пусть звено имеет длину L и симметрию относительно ГЦОИ. Положение центра масс (ЦМ) звена удобно задавать уже не в ГСК а, в только что созданной ЛСК, где началом координат является верхний конец звена, т.е. в ЛСК CS1. Тогда координаты ЦМ можно задать как CS1 [0, -L/2, 0]. Аналогично нижний конец звена можно задать в ЛСК CS1 [0, -L, 0].
Несмотря на то, что начало ЛСК CS1 совпадает с началом ГСК Global, следует иметь в виду что ЛСК CS1 принадлежит верхнему звену, а значит, может поворачиваться относительно точки Global [0, 0, 0]. Глобальная же система координат ГСК Global всегда неподвижна. Ее начало может и не совпадать с точкой сопряжения неподвижного звена (тем более, когда неподвижных звеньев в механизме несколько).
Рис. Системы координат двухзвенного физического маятника
25
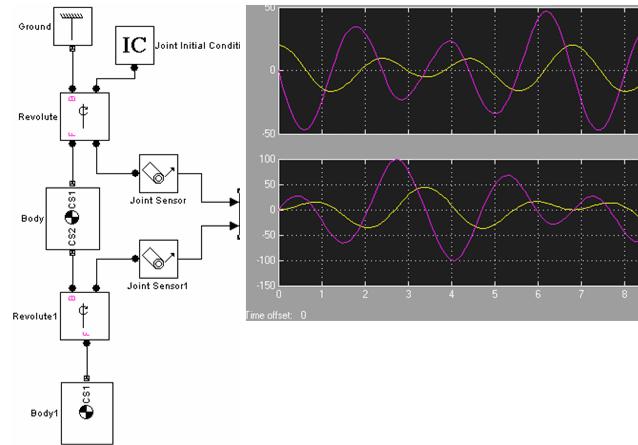
Помимо визуального наблюдения за свободными (при задании начальных условиях) или вынужденными (при наложении внешней силы) можно анализировать законы движения любой точки механизма. Для этого необходимо при задании координат звеньев указать координаты интересующей точки и к выходу соответствующего Simulink-блока подключить блок-датчик
(Sensor).
Датчики могут регистрировать как угловые колебания, так и линейные, причем как перемещение, так и скорость и ускорение. Выход с датчика обычно выводят на блок осциллографа Scope (см. рис. 4).
а) |
б) |
Рис. Модель двухзвенного физического маятника (а) для исследования законов движения его звеньев (б)
Порядок выполнения работы:
1. Ознакомление с пакетом SimMechanics.
1.1. Запустите MatLab и Simulink.
26
1.2. Откройте файл Phys_pend2.mdl. Проанализируйте приведенную модель двухзвенного физического маятника. Откройте функциональные бло-
ки и посмотрите на способы задания их параметров.
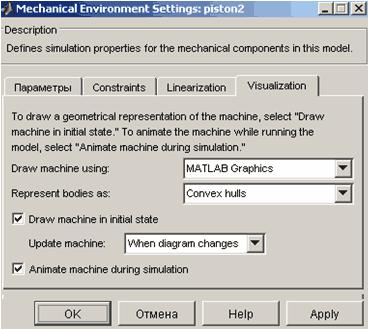
1.3. Вменю Simulation выберетепункт Mechanical Environment… . Здесь можно задать параметры механического моделирования (значения ускорения свободного падения, точности расчетов, способ отображения работы меха-
низма и пр.). Внесите изменения только во вкладку Visualisation (см. рис. 5).
1.4.Запустите модель, при этом наблюдая за колебаниями маятника.
1.5.Запустите модель с различными начальными условиями.
2. Моделирование кривошипно-шатунного механизма.
В данной лабораторной работе предлагается создать кинематическую модель кривошипно-шатунного механизма (рис. 6) и исследовать закон дви-
жения поршня.
Рис. Задание параметров визуализации механизма
27
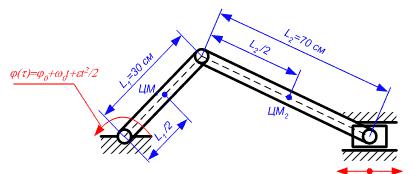
Рис. Кривошипно-шатунный механизм
Параметры кривошипа: Масса - 1 кг;
Моменты инерции относительно ГЦОИ - [Ix, Iy, Iz] = [50, 50, 300] г/см². Параметры шатуна:
Масса - 1.5 кг;
Моменты инерции относительно ГЦОИ - [Ix, Iy, Iz] = [80, 80, 500] г/см²
2.1Создайте новую Simulink-модель.
2.2Проектирование большинства механизмов начинается с неподвижного звена - земли. Для этого воспользуйтесь пакетом расширения SimMechanics - Bodies - Ground. В параметрах блока укажите координаты [0, 0, 0], это будет
означать, что координаты блока совпадают с началом ГСК. 2.3 Так как кривошип может совершать только вращение вокруг оси OZ, то возьмем в качестве блока сопряжения блок Joints - Revolute. В параметрах блока необходимо указать [0, 0, 1], что будет означать возможность вращения вокруг оси OZ.
2.4 Добавьте кривошипное звено в модель механизма, для этого воспользуйтесь блоком Bodies - Body. Внесите все необходимые данные о звене в параметры блока (см. рис. 7).
Ввод значений моментов инерции необходимо осуществлять в матричном виде [3 × 3] (см. рис. 7).
2.5. К уже спроектированной части механизма можно добавить привод (элемент, заставляющий механизм двигаться по определенному закону). Добавим вращение к сопряжению Revolute. Для этого в параметрах блока Revolute необходимо указать вход/выход для привода/датчика. При этом блок Revolute будет иметь еще один вход/выход. Кэтомувходунужноподсое-
динитьблок Sensors and Actuators - Joint Actuator.
28
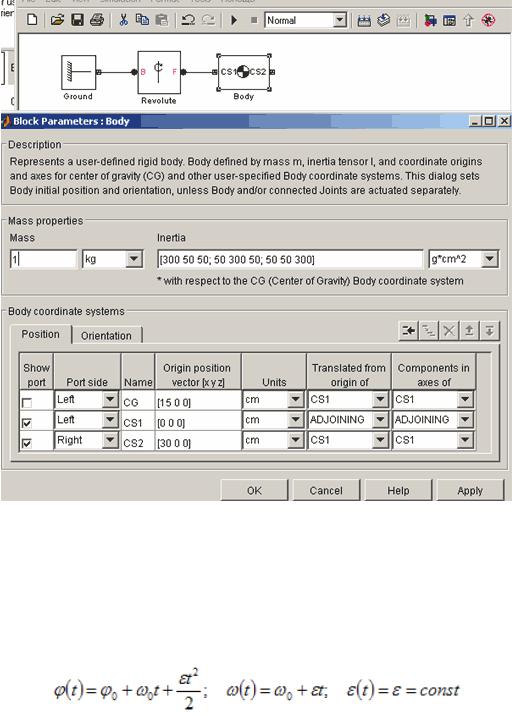
Рис. Параметры блока Body - при вводе данных о кривошипном звене
2.6. Для задания закона движения формируемого в звене JointActuator необходимо задать три параметра - вектора φ(t), ω(t), ε(t). Поэтому ко входу элемента JointActuator необходимо подать необходимые вектора. Так как величины φ0, ω0, ε - величины известные, то легко определить зависимости
φ(t), ω(t), ε(t):
Реализуйте приведенные зависимости в виде отдельной подсистемы, например, как показано на рис. 8.
2.7. Теперь можно запустить сформированную часть модели. Для этого необходимо выбрать в меню Simulation - MechanicalEnvironment … и далее указать параметры, показанные на рис. 5 и нажать кнопку ОК.
2.8 Самостоятельно доработайте модель кривошипно-шатунного механизма (см. рис. 9).
29
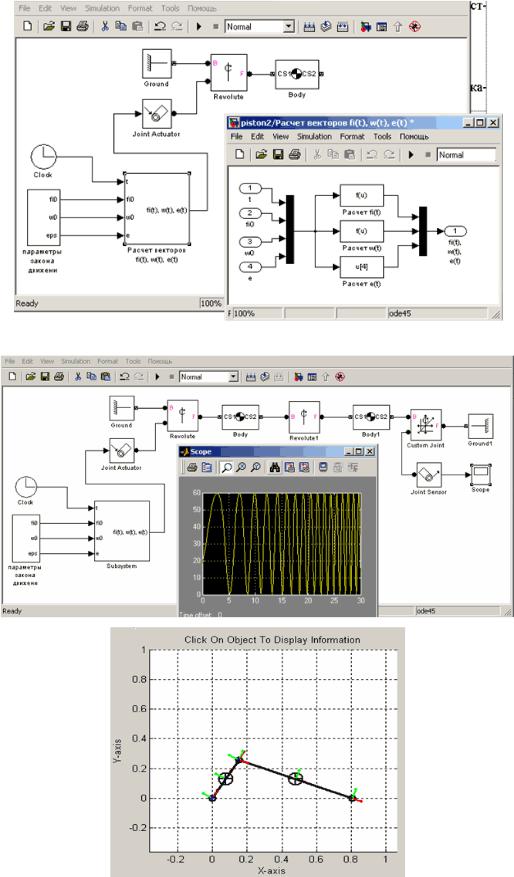
Рис. Добавление к модели привода и моделирование закона движения
Рис. 9 Окончательная модель кривошипно-шатунного механизма
30
