Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Микроволновые приборы и устройства.-1

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

997.79 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

Откуда к активной проводимости электронного потока Gэл требование име-

ет вид: -Gэл ³ G0 + Gн .

Следовательно, необходимо найти сумму проводимостей резонатора и нагрузки Gн , трансформированной к зазору. Коэффициент трансформации n прово-

димости нагрузки определяется соотношением

n = (1, 1 ¸ 1, 2 ) S n = 1, 1 5 × 0 , 0 8 = 0 , 0 9 2 . S r

Проводимость коаксиальной линии, являющейся нагрузкой [18], равна

	1	n2 = 0, 02 ×(0, 092)	2	= 2 ×10−2 ×8,5 ×10−3 = 17 ×10−5 = 1, 7 ×10−4		1
Gн =					,		.
	W
						Ом

Определим резонансную длину волны резонатора по формуле (1.22)

= pR1

4d h

×ln

= 3,14 ×0,5 ×

2 ×10

4 ×1 h

×ln 2

= 9,85 см.

5 d

Резонансную проводимость резонатора, используя формулу (1.27), найдем

h - d

R 2

−18 −1

= {

+ 2 ln

}

60L(см)

где Rs

= 0, 045

wmст

- поверхностное сопротивление.

2sст

L = μh ln

- эквивалентная индуктивность резонатора.

2p×3, 045 ×109 ×4p×10−7

= 1, 42 ×102

20, 7 ×10−5

, Ом.

2 ×5, 9 ×107

Z =

4P ×10−7 ×10−2

ln 2 = 2 ×10−9

×0, 693 = 1,386 ×10−9 Гн;

1Гн= 109 см.

1, 42 ×10−2 9, 35

+ 2 ln 2 = 0,135 ×10−4

, См .

2 ×3,14

×1, 386

G0 + Gн

= 1, 7 ×10−4 + 0,135 ×10−4 = 1,835 ×10−4 См

Откуда

-Gэл

> 1,835 ×10−4

См. . Для устойчивой работы генератора достаточ-

но.

Задача №6.( Расчет спиральной замедляющей системы [11,13])

Рассчитать геометрию спиральной однозаходной замедляющей системы ЛОВ для диапазона λср = 10 см . Лампа работает при ускоряющем напряжении, равном

890 В. Номер пространственной гармоники m = −1. Решение:

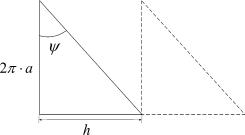
На рис.1.9. изображены: схематично спиральная ЗС, геометрические параметры, которые необходимо рассчитать.

Рис.1.9. Спиральная замедляющая система.

ψ - угол навивки спирали; δ - диаметр провода; 2a - диаметр спирали; h - шаг спирали.

Известно ускоряющее напряжение, можно определить коэффициент замедления волны в спирали Kз, а затем выразить коэффициент замедления через геометрию.

Kзам

(1.51)

Vфm

где

C –

скорость света;

Vфр –

фазовая скорость p-ой гармоники.

C = λ × f , V

= λ

× f и V

; C = ω .

фm

βm

K зам

(1.52)

λз

Kзам

βm × a

(1.53)

k × a

где

a –

радиус спирали, к- волновое число свободного пространства.

Фазовая скорость волны первой отрицательной пространственной гармоники

должна быть примерно равна скорости электронного потока.

Vфm @ V0

V0 –

скорость электронов определятся из (1.2), фазовая скорость p-ой гармо-

ники равна V

, тогда

2π ×

фр

β p

β0 +

×U0

(1.54)

2π × m

β0 +

Т.к.

505

, то коэффициент замедления (1.51) K зам =

505

= 17

Vфm

890

Определим угол намотки спирали ψ , используя соотношений (1.53)и (1.54)

.Здесь m = −1;

т.к. для нулевой гармоники в области наших частот дис-

2π × a

β0

персия отсутствует. Тогда

Kз

2π ×a

[1+

(-1)

]

(1.51,б)

Vф

a ×k

Из рис.1.10 запишем
	2π × a	= ctgψ	(1.55)

	h

Рис.1.10 Развертка спирали на плоскость.


Значение ctgψ	берется большим, при ψ ® 0 , т.к. при этом снижается U раб ;
увеличивается N - число длин волн вдоль оси спирали ,уменьшается рабочая
							1
длинна лампы L. Для однозаходной спирали							[15] величина 2 P			P 6 . Это видно
									a × K
из равенства (1.55),	т.к. при	1	= 2 ;	C	=	2π × a		, а это соотношение близкое или

		a × k		Vф			h

равное значению нулевой гармоники, которая при этом возбуждается быстрее, чем первая отрицательная гармоника.

При

P 5 ¸ 6 величина сопротивления связи уменьшается, а это уменьшает

a × k

выходную мощность P.

Задаем

= 3 , тогда радиус спирали:

a =

= 0.53 см ;

= ctgψ (-2)

(1.56)

6π

18.8

Vф(−1)

Минус (-) – показывает, что обратная гармоника, но при расчетах

его можно

опустить.

= ctgψ = 8.5 ,

ψ = 60 40',

a = 0.53 см .

Найдем шаг спирали h из (7) и оценим диаметр проволоки. Т.к.

2πa/h=8,5, то			h =	6.28 × 0.53				= 0.39 cм .

			8.5
При выполнении 0.3 £ δ £ 0.5							минимум потерь в проводниках системы. Берем
δ = 0.4				h
	δ = 0.4 × 0.39 = 0.156 cм .
h
Оценим сопротивление связи спирали при r = a , воспользовавшись формулой
[15]	Rсв (a) =		16.7		×		1		(1.57)
			- 0.923)2			a × K
	(	1

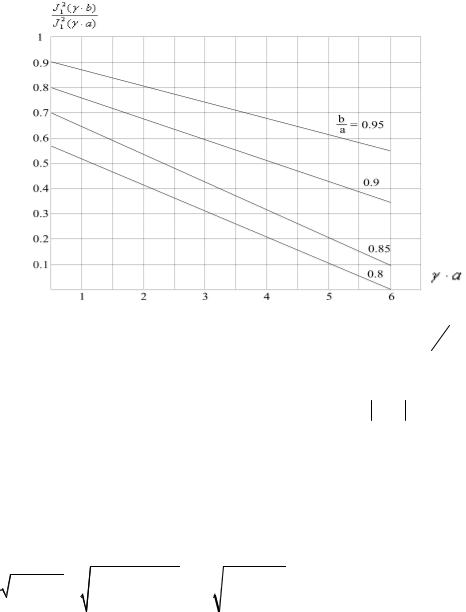
Рис.1.11. Поправочные коэффициенты для вычисления действующего значения волнового сопротивления при различных b a .

Это сопротивление связи определено на самой спирали, но т.к. пучок проходит на некотором расстоянии от спирали, равном b - a , то следует в форму-

лу (1.57) внести поправку, в виде:

Rсв (b) = Rсв (a)

J12 (γ b)

J12 (γ a)

где

J0 – функция Бесселя;

γ - фазовая постоянная распространения волн в на-

правлении радиуса. Смысл тот же, как для гребенки у величин ξ1 и h1 .

= ω

» ω ×

6.28 ×3×109

γ =

= (

)2 - (ω )2

(

)2 -1

β 2 - K 2

= 5.6

C V

5.95 ×105 × 29

фm

По графику рис.1.11 определим поправочный коэффициент для

= 0.9 .

J12 (γ b)

Rсв

r =b =

16.7

× 3 × 0.38 = 5.6

Ом

=0.9 = 0.38 ,

J12 (γ a)

(3 - 0.923)2

U 2

Найдем волновое сопротивление спирали, пользуясь формулой W (U ) =

по

напряжению, W ( J )

по току.

J 2

376 × β0 × J 02 (γ a)

π × K ×γ × a × F (γ a)

где

J0 – функция Бесселя нулевого порядка.

Или более простая формула волнового сопротивления спирали в цилиндре,

что практически всегда выполняется

W = 60K зам J 0 (γ a)N 0 (γ a) ,

где

N0 – функция Неймана нулевого порядка.

m = −1,

Для нашего случая имеем:

W = 60 ×17 × 0.027 × 0.34 = 9.3 Ом

Как видно волновое сопротивление не равно сопротивлению связи.

Вывод: Определена геометрия, параметры работы в ЛОВ на m = -1, Rсв и W спирали для замедляющей системы помещены в таблицу 1.1.

Таблица 1.1

2a	h	δ	ψ	Rсв	b	W	λ	U0
2a	h	δ	ψ	Rсв	b	W	λ	U0

1.06 см	0.39 см	0.156	60 40'	5.6 Ом		9.3 Ом	10 см	890 В
		см

Задача №7 (Рабочий диапазон замедляющей системы встречные штыри)

В каком диапазоне длин волн может работать замедляющая система типа встречные штыри (рис. 1.12), если рабочее ускоряющее напряжение изменяется в пределе 324 B ÷1600 B . Замедляющая система используется в ЛОВО на

длина штыря составляет 20 мм, период h=2 мм.

Решение:

Для решения этой задачи необходимо воспользоваться условием фазового

синхронизма.	Vф @ V0	=	C
			K зам

Для нулевой гармоники это условие можно записать в другом виде

h + b	=	C	= K зам0	(1.58)

h		Vф0

Для m-ой гармоники фазовое условие можно получить из соотношения для постоянной βm

βm = β0 + 2π × m 2h

Здесь

β0 =

2π × f

2π

Vф0

2π × f

2π × m

×λ

Vфm

Vф0

+ λ ×m

Vфm

Vф0

(1.59)

(1.60)

Из (1.58) и (1.60) имеем

C = h + b + λ × m = h + b - λ

Vф1 h 2h h 2h

Но, учитывая отрицательный знак перед Vф(−1) и для ЛОВ на -1-ой гармоники

имеем:	С	= -(	λ	-	h + b	) .	(1.61)
	Vф(−1)
			2h h

Используя (1.61) найдем выражение в общем виде для определения диапазо-

на длин волн. Для расчетов следует брать		C	, тогда
	Vф(−1)

С= 505 = λ - λ + b .

				Vф(−1)				U 0 2h h
Т.к. два напряжения заданы, то определяем большую и малую длину волны
(	505	+ λ + b ) × 2h = λ ;		(	505		+	20 + 2	) × 0.2 × 2 = λ ;		(	505		+	20 + 2	) × 0.2 × 2 = λ
(		+ λ + b ) × 2h = λ ;		(			+		) × 0.2 × 2 = λ ;		(			+		) × 0.2 × 2 = λ	2
	U 0	h		1600		2				1	324		2				2
	U 0	h		1600		2					324		2
(12.6 + 11)0.4 = 9.44 см ;			(28 + 11)0.4 = 15.6 см;
Ответ: 9.44 ≤ диапазонλ ≤ 15.6

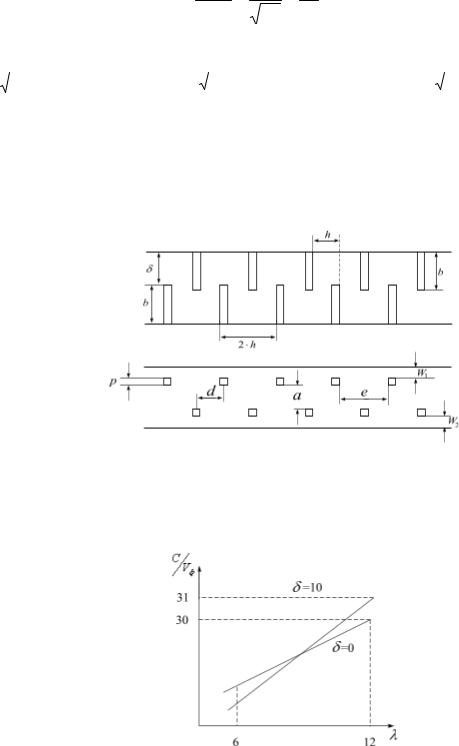
Задача №8. (Расчет геометрии ЗС типа встречные штыри )

Решение проводится в общем виде для любой гармоники [14].

Рис.1.12. Замедляющая система типа встречные - штыри.

Размер δ (рис.1.13) не влияет на дисперсионные свойства замедляющей системы. Поэтому размером δ можно при расчете геометрии задаться согласно технологии. Точно также поступают и с размерами и m, b, a, W.

Рис.1.13.Зависимость коэффициента замедления от длины волны при разных размерах δ.

Считая, что волна движется по известному пути между штырями, со скоро-

стью света С, имеем:

b + h

Vф0

β0

2π ×C

2π × f

λ ×Vф0

Vф0

2π ×C

2π × m

λ ×V

фm

ф0

фm

здесь m = 0, ±1, ± 2...

. Т.к. βm = β0

2π × m

получаем

βm =

2π ×C

или

m ×λ

λ ×Vфm

b + h

Vф0 2h

Vфm h

Это выражение описывает достаточно хорошо для практических целей дисперсионные характеристики однорядных и двухрядных замедляющих систем типа встречные штыри.

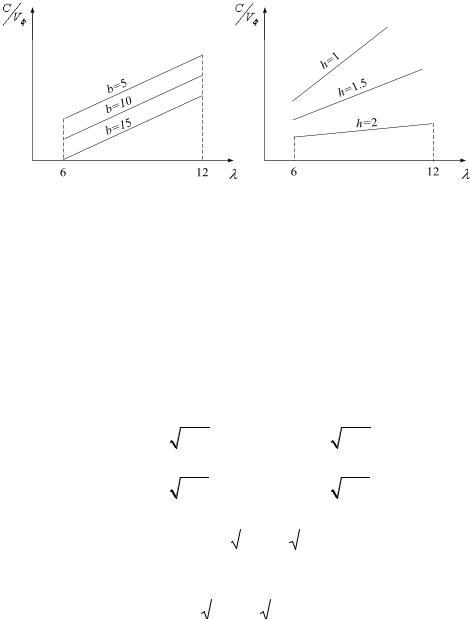
При изменении b кривые смещаются параллельно себе.

Рис.1.14.Поведение коэффициента замедления в диапазоне длин волн для разных значений b и h.

Таким образом, варьируя h и b, можно получить желаемое замедление при данной длине волны λ и наоборот. От остальных параметров характеристики почти не зависят.

Выбор оптимальных размеров замедляющих систем.

Пусть задан диапазон λmin - λmax и диапазон U min и U max .Таким образом из

формулы (3.4) можно определить m, h. Задается номер гармоники, пусть m = −1. Кривая электронной настройки дает λmin -U max и λmax -U min .

= - h + b + λmin

= 505

5.95 ×105 ×

Umax

h + b

λmax

505

= -

5.95 ×105 ×

Umin

λmax - λmin =

505

U min

U max

2h =

λmax - λmin

505

U min

U max

где h – период замедляющей системы типа встречные штыри.

Из

λmax - 2

b + h

2h ×505

2h ×

Umin

λmax − λmin

2b = λmax

- 2h - 2h ×

505

= λmax - 2h ×(1-

505

) = λmax -

(1-

505

) =

505

Umin

Umax

λmax

× (

505

) - λmax +

505

× λmax + λmin - λmax

505

U min

U max

U min

505

U min

U max

λmin × (1 +

505

) - λmax × (1 +

505

)

U min

U max

= 2b

505

U min

U max

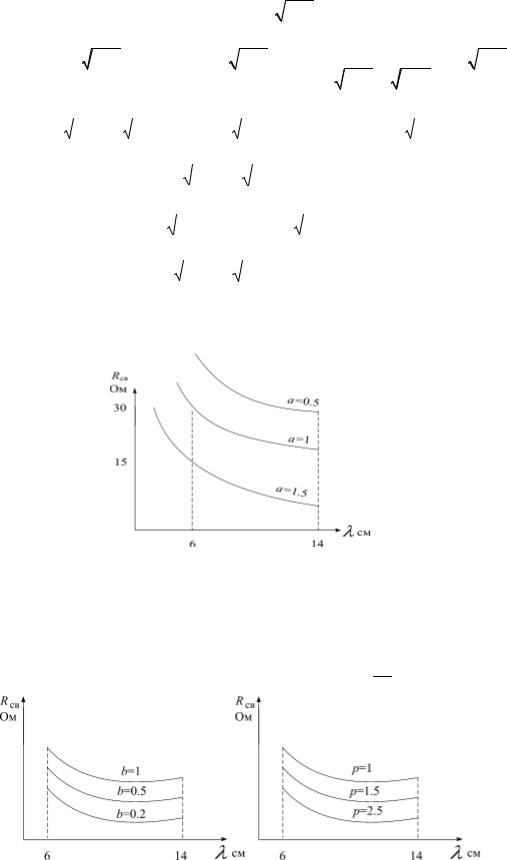
Сопротивление связи Rсв увеличивается при уменьшении расстояния между ряда-

ми штырей системы типа встречные штыри- a ( рис.1.15), а дисперсия от a не зависит. Исходя из этого, величину a нужно выбирать минимальной.

Рис.1.15 Зависимость сопротивления связи от расстояния между рядами штырей a в замедляющей системе.

Однако, если a выбирается минимальной, то при заданной величине тока J прибора и плотности тока эмиссии jk , то высота электронного потока b должна

быть определенной, согласно известному соотношению J £ jk .

Рис.1.16. Влияние на сопротивление связи размеров p, b.

Хотя, сопротивление связи Rсв увеличивается с ростом h и уменьшением р,

свойства дисперсионные остаются неизменными. Кажется можно увеличивать h и уменьшать р, но при этом ухудшаются тепловые и механические параметры замедляющих систем. Поэтому h и р выбирают из требований механической проч-

ности конструкции ЗС прибора и ее теплового режима, Обычно p @ b @ h .

Из конструктивных и технологических соображений выбирают δ и W .

δ = 0.5 ÷1 мм W F h

Длина замедляющих систем определяется параметром усиления, который зависит от длины волны в ЗС, от числа N замедленных длин волн λз, уложившихся вдоль неё (см. раздел 3, далее)

K ус = f (N ×λ) .

5.2.Индивидуальное задание №2

Клистроны. - раздел программы – 2.3.1.

5.2.1. Основные вопросы теории

В этом задании студенту необходимо провести расчет параметров и характеристик (КПД, коэффициента усиления, коэффициента преобразования, полосы рабочих частот и пр.) усилителей, генераторов, умножителей частоты на клистронах при различных условиях.

Клистроны по особенностям группировки электронного потока делятся на два типа: пролётные и отражательные. В пролётных клистронах группировка электронов происходит в пролётном пространстве, называемом пространством дрейфа, а в отражательных - в пространстве тормозящего поля, расположенном между отражателем и резонатором. Процесс модуляции скорости переменным напряжением резонатора в обоих типах клистронов одинаков. Скорость электронов [2,3] после прохождения первого резонатора определяется соотношением:

V = V0 + V1 × sin ω × t1 ,

(2.1)

где V0 - скорость на входе резонатора (1.2), V1 -амплитуда переменной составляющей скорости на выходе резонатора, имеет вид

V 1	= M 1	V 0		U 1		,	(2.2)
		2	U		0

где M1 - коэффициент взаимодействия зазора первого резонатора (1.13), U1 - амплитуда переменного напряжения на первом резонаторе, U0 - ускоряющее напря-

жение на пушке и резонаторе.

Фаза прилёта каждого электрона во второй резонатор или вторичного прохождения в отражательном клистроне ω ×t2 , без учета влияния пространственного

заряда, в зависимости от фазы вылета из первого резонатора ω·t1 определяется уравнением:

ω×t2 =θ +ω×t1 -X×sinω×t1 .

(2.3)

Здесь θ = ω × S угол пролёта (1.17) немодулированным по скорости электроном

между резонаторами, расположенными на расстоянии S один от другого в пролётном клистроне; Х- параметр группировки.

Для отражательного клистрона, если расстояние между сетками резонатора d, а между резонатором и отражателем D; U R -напряжение на отражателе клистрона,

то угол пролета в пространстве тормозящего поля - Ө0 , а в зазоре -Өз, и общий угол пролета определяется выражением


θ = θ0	+θЗ =	2m	ω × D ×V0		+ ω × d .	(2.4)

		e U0 +		UR
					V0

Величина параметра группирования для пролётного клистрона:

X = ω × S

M1 ×U1

= 0,5θ × M1

×ξ = θ

;

(2.5а)

V0 2U0

для отражательного клистрона:

ω × D

- ω ×d ) ,

X = (θ

-θ

)

= 0,5θ × M

×ξ = V (

(2.5б)

e U

V 2

здесь ξ = U1 - коэффициент использования напряжения первого резонатора;

ω - рабочая круговая частота.

Конвекционный ток i2 , поступающий во второй резонатор пролётного клис-

трона, или поступающий в резонатор отражательного клистрона при возвращении электронов из пространства группирования, равен:

			∞
i2 = I0 × kC /( 1 - X cos ω ×t1 ) = I0 + 2 × I0 × kc ∑ Jn ( nX )×cos( n( ω ×t2 -θ )) ,				(2.6)
			n=1
причем I0 -ток на входе в резонатор-модулятор; кс - коэффициент прозрачности
сеток резонатора, равный kC	=	S0	- отношению площади отверстий сеток зазора
сеток резонатора, равный kC	=		- отношению площади отверстий сеток зазора
		SC

резонатора S0 к площади сечения зазора – S C; Jn(nX)- функция Бесселя первого рода n-го порядка от аргумента nX; n-номер гармоники.

Оптимальные значения параметров группировки и соответствующие им значения функции Бесселя для разных гармоник приведены в таблице 2.1.

Таблица 2.1.

Оптимальные значения параметров группирования и функций Бесселя для различных гармоник.

Параметр				n-номер гармоники
	1	2	3	4	5	8	10		15	20
Xopt	1,84	1,53	1,4	1,35	1,28	1,22	1,2		1,13	1,1
Jn	0,58	0,487	0,434	0,35	0,345	0,32	0,26		0,25	0,24
Наведённый во внешней цепи ток для n-ой гармоники Iнn								, согласно (1.9) ра-
вен:
			Iнn	= -Ikn × M 2n .							(2.6а)

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20231.29 Mб17Микроволновая техника. Объемный резонатор на отрезке волновода.pdf
#
05.02.20231.34 Mб6Микроволновая техника. Прямоугольный волновод.pdf
#
05.02.20233.61 Mб9Микроволновая техника..pdf
#
05.02.2023485.7 Кб12Микроволновая электроника.-1.pdf
#
05.02.2023793.34 Кб12Микроволновая электроника..pdf
#
05.02.2023997.79 Кб7Микроволновые приборы и устройства.-1.pdf
#
05.02.20235.77 Mб23Микроволновые приборы и устройства..pdf
#
05.02.2023836.9 Кб9Микромехатроника. Наномехатроника-1.pdf
#
05.02.2023359.69 Кб9Микромехатроника. Наномехатроника.pdf
#
05.02.2023205.11 Кб9Микропроцессорная техника в мехатронике и робототехнике.-1.pdf
#
05.02.2023144.11 Кб13Микропроцессорная техника в мехатронике и робототехнике.-2.pdf