
Микроволновые приборы и устройства.-1
.pdf
Рисунок 1.4. Ячейка магнетронного резонатора.
Размеры резонатора видны на рис. 1.4, причем
С |
0 |
= |
εαh |
, |
L |
= |
μπR 2 |
. |
|
|
d |
0 |
|
h |
|||
|
|
|
|
|
|
|
Перестройка частоты объемных резонаторов осуществляется изменением одного из размеров: либо высоты резонатора ℓ (рис.1.1) либо диаметра, посредством погружения металлических стержней в область с магнитным полем, либо изменением высоты зазора d (рис.1.1).
Собственная добротность тороидальных резонаторов (для других типов резонаторов см. [9]) вычисляется по формуле
|
|
2m |
|
|
l ×ln |
b |
|
|
|
|
|
|
|||
Q0 |
= |
× |
|
a |
|
|
|
. |
(1.26) |
||||||
|
|
|
|
|
|
||||||||||
dm |
|
|
b |
1 |
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
ст |
|
2 ln |
|
+ l |
|
+ |
|
|
|
|
||
|
|
|
a |
|
a |
|
|
||||||||
|
|
|
|
|
|
b |
|
|
|
|
|||||
Эквивалентное резонансное сопротивление |
тороидальных резонаторов [9] |
||||||||||||||
R0 = |
RS |
|
l0 |
2 |
L - d |
+ |
L |
+ 2 ln |
b |
, |
Ом, |
(1.27) |
|||
|
|
|
|
|
|
|
|
|
|
||||||
2p |
3 |
60L0 |
|
b |
|
||||||||||
|
|
|
|
a |
|
|
a |
|
|
|
|||||
где RS |
= |
wmст |
- поверхностное сопротивление; все геометрические размеры |
|
|
2s |
|
на соответствующих рисунках.
Резонансный микроволновый прибор как элемент схемы [2,16]
Условия самовозбуждения СВЧ генераторов с резонансными колебательными системами имеют вид:
|
G |
0 |
+ G |
e |
+ G′ |
= 0 |
|
|
|
н |
(1.28) |
||
|
|
|
|
|
|
|
|
B0 + Be + B¢н = 0 |
|||||
гдеG0 , B0 - активная и реактивная проводимость колебательной системы; |
||||||
Ge , Be - активная и реактивная проводимости электронного потока; |
||||||
Gн |
, Bн - активная и реактивная проводимости нагрузки, трансформирован- |
|||||
′ |
′ |
|
|
|
|
|
ной к области движения носителей заряда (зазора).
Мощности отдаваемая электронным потоком Ре, выделяемая в контуре Рк и в нагрузке Рн определяются, если известна амплитуда переменного напряжения Um, соотношениями
Pе = |
1 |
U m2 |
0 G e , |
Pн = |
1 |
U m2 |
0 G ¢н , |
Pk |
= |
1 |
U m2 |
0 G k . |
(1.29) |
|
|
|
|||||||||||
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|||
21
Трансформированные активная Gн |
и реактивная Bн − проводимости на- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
′ |
|
|
|
грузки к зазору резонатора определяются в виде |
|
|
|
|
|
||||||||||||||||||||||
G¢ |
= |
|
|
G н |
|
= |
|
Yc |
|
= G |
|
Q0 |
; |
B¢ = |
BH |
= B |
|
Yc |
= |
BH G 0 Q0 |
, (1.30) |
||||||
(K T )2 |
|
|
|
|
|
(K T )2 |
H G H QBH |
|
|||||||||||||||||||
|
н |
|
|
|
|
QВН |
|
0 QВН |
H |
|
|
G H QBH |
|
||||||||||||||
где (КТ)2 – коэффициент трансформации; |
|
|
|
|
|
|
|
||||||||||||||||||||
Y = |
f 0 |
|
( |
dB |
) |
f =f0 |
|
- характеристическая проводимость резонатора; |
(1.31) |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
c |
|
2 |
|
|
|
|
df |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
G |
|
= G |
|
|
+ G¢ |
= |
YC |
-суммарная активная проводимость резонатора. |
|||||||||||||||||||
п |
0 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
H |
|
|
QH |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Мощность генератора в нагрузке Pн |
определяется амплитудой установив- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
шихся колебаний Um 0 и проводимостью нагрузки Gн . |
|
|
|
||||||||||||||||||||||||
Частота генерируемых колебаний определяется собственной резонансной частотой колебательной системы f0 , нагруженной добротностью этой системы
Qн , реактивной Bе и активной Ge |
электронными проводимостями |
|
||||
|
|
|
|
B e |
|
|
f v |
= f 0 |
1 |
+ |
|
. |
(1.33а) |
|
||||||
|
|
|
|
2Q н G e |
|
|
В случае учета влияния нагрузки на частоту генератора следует использовать формулу при условии Gн=1
fг = f 0 (1 - |
Bн |
) . |
|
|
|
|
|
(1.33б) |
|
|
|
|
|
|
|||||
|
2Qвн |
|
|
|
|
|
|
|
|
Величина реактивной проводимости в относительных единицах определя- |
|||||||||
ется соотношениями: |
|
|
|
|
|
|
|
||
Bнмах = Bнмин = ± |
(K CB )2 |
-1 |
. |
|
(1.34) |
||||
|
K СВ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Изменение частоты генератора при изменении нагрузки, выраженное в ве- |
|||||||||
личинах Ксв, определяется в виде Df = ± |
f0 |
|
(K СВ ) 2 -1 |
, |
|
||||
Qвн |
|
|
|||||||
|
|
|
|
|
2K СВ |
|
|||
диапазон изменения частоты под влиянием нагрузки определяется формулой
Dn = |
f |
0 (K СВ )2 -1 |
= FЗ ×1,2 × |
(K СВ ) 2 |
-1 |
, |
(1.35) |
|||
|
|
|
|
|
|
|
||||
Qвн 2K СВ |
K СВ |
|
||||||||
|
|
|
|
|
||||||
здесь FЗ = 0,417f0/Qвн – |
параметр затягивания частоты. |
(1.36) |
||||||||
Замедляющие системы (ЗС) для микроволновых приборов должны иметь заданную величину коэффициента замедления Kз, высокое сопротивление связи Rсв, определенный характер дисперсии Vф(f )и величину крутизны дисперсионной характеристики, необходимую для взаимодействия с электронным потоком конфигурацию электромагнитного поля и хороший теплоотвод.
Расчет этих параметров проводится тремя методами: методом многопроводных линий, полевым методом и методом эквивалентных схем. Последний метод наиболее прост, часто применяется и дает достаточно хорошее совпадение
22
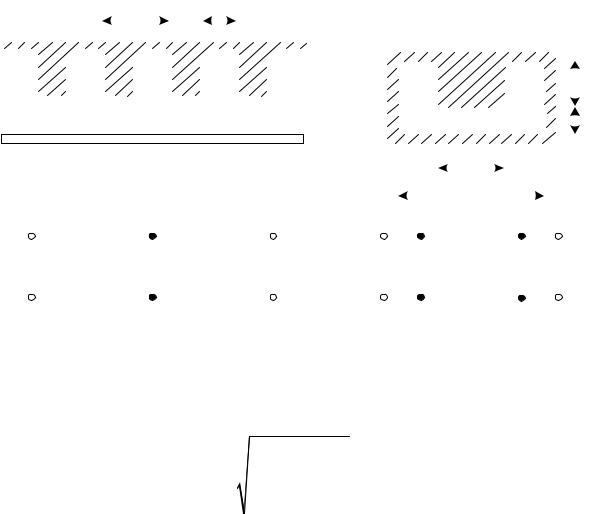
теоретических и практических результатов. Применим его для разных замедляющих систем.
Гребенка в волноводе (рис.1.5) на эквивалентной схеме [15,18] представляется цепочкой четырехполюсников П- или Т-образных ячеек.
Фазовый сдвиг ϕ0 волны на ячейку замедляющей системы в зависимости от
частоты (определяется геометрическими и электрическими параметрами замедляющей системы) называется дисперсионным уравнением. Для эквивалентных схем, представленных на рис 1.6, дисперсионное уравнение [11] имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos j = 1+ |
C2 |
× |
1- w2 |
. |
(1.37) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2C |
|
w |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис 1.5 – Гребенчатая замедляющая система в волноводе и ее эквивалентная схема: а) Т – образная ячейка; б) П – образная ячейка.
Полоса рабочих частот П и Т – образных схем может быть определена из (1.35) как полоса, ограниченная частотами отсечки полосового фильтра
|
|
ω 12 + |
|
C 2 |
|
|
ω 22 |
|
|
|
|
4 C |
|
|
|
||||
ω ϕ 0 = π |
= |
|
1 |
|
|
, |
(1.38) |
||
1 + |
|
C |
2 |
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
4 C 1 |
|
|
|
|||
|
|
|
|
|
|
|
|||
|
ω ϕ 0 = 0 = ω 2 , |
|
|
|
|
|
|||
здесь C2 - емкость связи между плоскостью (катодом) и штырем (например, сегментом в магнетроне) ЗС;
C = |
4b2 |
, L = pbln - индуктивность и емкость паза щелевого резонатора. |
|||||||
p2 L |
|||||||||
1 |
|
1 |
w |
|
|
||||
Соотношения для определенияw1 , w2 (частоты отсечки) следующие |
|||||||||
w2L |
C |
2 |
= 1; |
w2L C = 1 ; |
|||||
2 |
2 |
|
|
|
1 |
1 |
1 |
||
23
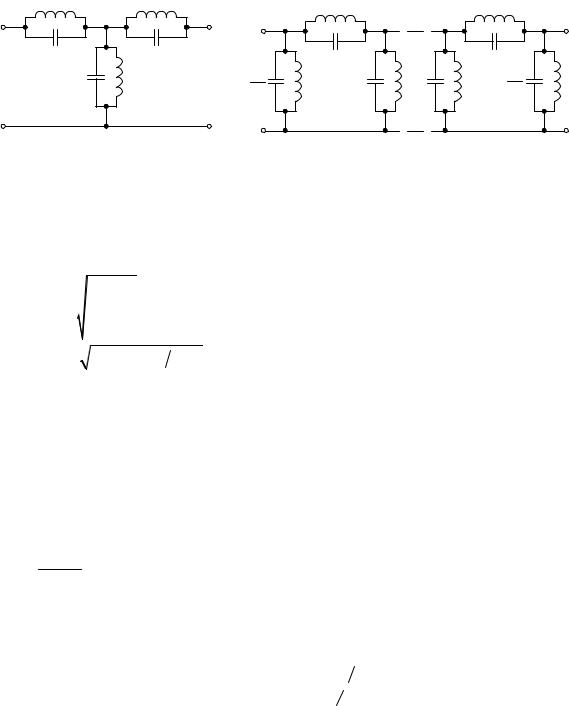
ω − рабочая частота;
L1,2 , C1,2 − параметры (индуктивности и емкости) эквивалентной схемы типа Т или П.
|
|
L1 |
|
|
L1 |
|
или С2 |
|
C1 |
|
|
C1 |
|
2L2 |
C2 |
L2 C2 |
L2 |
C2 |
2L2 |
|
2 |
|
|
|
|
2 |
|
|
Т – схема |
|
|
|
|
|
|
П – схема |
|
|
|
|
|
|||||
|
Рис. 1.6 |
|
Эквивалентная схема ЗС в виде эффективных индуктивностей и |
|||||||||||||||
|
|
|
|
|
|
емкостей для П- и Н- образных схем. |
|
|
|
|
|
|
||||||
|
Волновое сопротивление П – или Т – образной эквивалентной схемы со- |
|||||||||||||||||
гласно [15] равны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZП = |
|
Z1Z2 |
|
для П – |
образной ячейки, |
|
|
|
|
|
|
|
|
||||
|
1+ |
Z1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
4Z2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
для Т – образной ячейки. |
|
|
|
|
(1.39) |
|||||
|
ZТ = |
|
Z1Z2 (1+ Z1 |
4Z2 ) |
|
|
|
|
||||||||||
|
Величина коэффициента передачи g , для П или Т – |
|
образной эквива- |
|||||||||||||||
лентной схемы, определяется соотношением |
|
|
|
|
|
|
|
|
||||||||||
|
ch g = 1+ |
Z1 |
|
, где |
g = b0 ± jj0 ; |
|
|
|
|
|
|
(1.40) |
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2Z2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
tg |
j0 |
× w13 × |
1 |
|
|
|
где b - коэффициент потерь мощности на ячейку ЗС. b = |
2 |
|
, Нп; |
|||||||||||||||
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
Q |
w |
w1 -1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w2 |
|
|
здесь Q = p×lb0 - добротность ячейки ЗС типа щелевой резонатор, aТ - коэффици-
aТ ×l02
ент потерь в стенках ячейки замедляющей системы.
Сопротивление связи гребенки на m − ой гармонике [11] определяется соотношением
|
Z 12 |
|
1 |
|
s in (b |
0 l n |
2 ) |
2 |
|
|||
R св p = |
|
|
× |
|
|
|
|
|
|
|
, |
(1.41) |
2 |
Z T |
D |
2 |
b m |
l n 2 |
|
||||||
|
b m |
|
|
|
|
|
|
|
||||
24
где |
Z1 |
= |
|
1 |
|
|
- сопротивление последовательного элемента четырехполюс- |
|||||||||||||||
jwC1 |
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
- w12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
C2 |
- w12 - |
C2 |
× w22 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ника (рис 1.5); |
|
ZT = |
|
|
4C |
w2 |
|
4C |
w2 |
|||||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
- волновое сопротивление четырех- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
w |
|
|
|
2 |
-1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
C1C2 1 |
- w12 |
|
w22 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
w |
|
|
|
||||
полюсника;
bm = b0 |
+ |
2πm |
- фазовая постоянная распространения волны в ЗС на m − ой гармони- |
||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m = ±1, 2,3,... |
|
||||
ке; jm = j0 + 2pm - фазовый сдвиг; номер гармоники |
|
||||||||||||||||||||||||
|
Параметры индуктивности и емкости определяют из уравнений |
||||||||||||||||||||||||
|
C2 = |
eS |
= |
e0 w (D - ln ) |
[ф], |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
d |
|
|
|
d |
|
|
|
|
|
|
|
w (b + d) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
l22 |
|
|
|
|
l22 pd |
|
|
|
|
p |
2 |
|
(a - w ) pd |
p(b + d)(a - w ) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
, |
|||||||||
|
L2 = |
|
|
= |
|
|
|
= |
|
|
|
|
|
= |
|
||||||||||
|
(4p)2 C2 |
(4p)2 w (D - ln ) |
|
|
|
16p2 w (D - ln ) |
|
16 (D - ln ) |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
где l2 |
= lкрП,Н = p |
w (b + d) |
(a - w ) критическая длина волны волновода определяет- |
||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ся сечением ЗС. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Если использовать полевой метод [17]для получения дисперсионного урав- |
||||||||||||||||||||||||
нения [2] гребенки, то получим уравнение вида |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
× tg (k × b ) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
x × b × th |
|
|
× x × b |
= k × b |
|
(1.42) |
|||||||||
|
|
|
|
|
|
|
|
|
|
b |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где x −поперечное волновое число; |
|
k − фазовая постоянная распространения вол- |
|||||||||||||||||||||||
ны свободного пространства; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Остальные геометрические параметры видны на рис.1.5.
Из уравнения (1.42), при известной геометрии и заданной постоянной распространения в свободном пространстве k , определяется поперечное волновое число х, а, следовательно, фазовая постоянная волны β в ЗС и коэффициент замедления KЗ :
b = |
|
|
|
= k |
1- (x k )2 |
|
|
|
|||
k2 - x2 |
|
||||||||||
KЗ = b |
|
|
|
|
. |
|
|
||||
= 1- (x k )2 |
|
||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
Сопротивление связи на нулевой гармонике ( m = 0 ), полученное в [17] по- |
|||||||||||
левым методом, определяется в виде |
|
|
|
|
|
|
|||||
R св = |
|
|
Z 0 2 x 3 s h 2 ( x × y ) |
|
|||||||
|
|
|
, |
(1.43) |
|||||||
b |
3 k c h ( |
2 x d ) - 2 x d |
|||||||||
|
|
|
|
|
|
|
|
|
|||
25
где Z0 = 377 Ом.
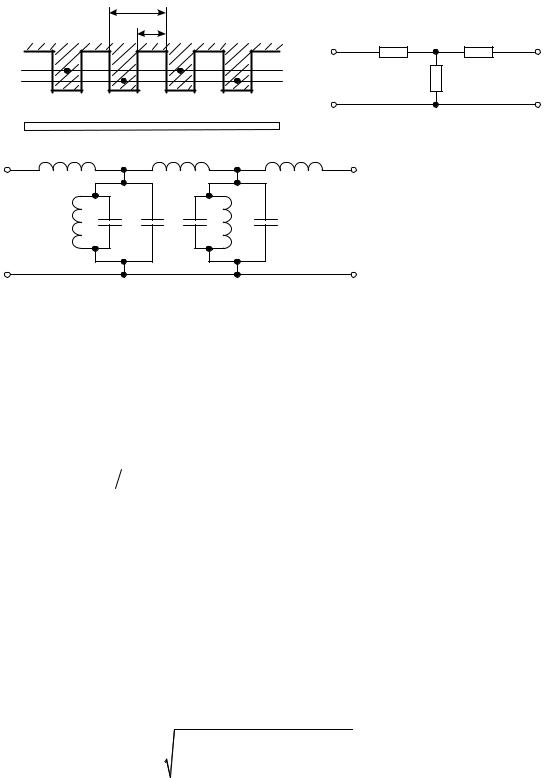
Гребенка со связками [10,11] используется в магнетронах и платинотронах. Штыри (в платинотронах - ламели) гребенки последовательно через один соединены электрически друг с другом проводниками, называемыми связками
(рис.1.7)
Рис 1.7. Гребенчатая система со связками и ее эквивалентная схема.
Система (рис. 1.7) характеризуется аномальной дисперсией в полосе пропускания. Эквивалентная схема (рис 1.7) позволяет записать
|
|
Z1 = jωLсв , Z2 |
= |
|
Z |
, |
(1.44) |
|
|
|
|
− jωZCсв |
|||||
|
|
|
1 |
|
|
|||
|
1 |
|
|
|
|
|
|
|
где |
Z = |
|
− |
входное сопротивление резонатора относительно то- |
||||
j(ωC1 −1 (ωL1 )) |
||||||||
чек подключения связок к ламели (например, точек A − D ,на рис.1.7);
C1 , L1 − эквивалентные параметры щелевого резонатора;
Lсв , Cсв - эквивалентные индуктивность и емкость связок на период системы
D.
Нижняя частота системы (фильтра) определяется из условия параллельного
резонанса: ( Z |
2 |
= ∞ ); |
ω = ( jZC |
св |
)−1 |
, а верхняя - из условия последовательного резо- |
|||||||||||||
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|||
нанса |
|
|
Z |
+ |
jωLсв |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1− jωCсвZ |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Параметры Т – образной схемы: |
|
|
|
|
|
|
|||||||||||||
волновое сопротивление |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
jωL |
св |
|
|
|
|
|
|
|
|
|
ZT = |
|
jωLсв |
|
|
+ |
|
|
, |
(1.45) |
|||||
|
|
|
|
|
|
− jωZCсв |
4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
величина постоянной передачи имеет вид
26
|
|
|
|
cos j0 |
= 1+ jωLсв (1- jwCсвZ) |
|
(1.46) |
|||||||||||
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
Z |
) + |
jwL |
|
|
; |
|
|
|
|
|||
ZT = |
|
jwLсв 1- (w w |
|
4 св |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
cos j |
|
= 1+ |
jωLсв |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
1- w |
w |
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
||
здесь j0 - фазовый сдвиг на период ячейки вдоль связок в направлении |
||||||||||||||||||
движения потока энергии. А фазовый сдвиг в пространстве взаимодействия в на- |
||||||||||||||||||
правлении движения электронного луча будет q0 = p - j0 |
и, следовательно, фазовая |
|||||||||||||||||
скорость волны в направлении движения электронного потока равна |
V = |
ωD . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ф |
p - j0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Располагая величиной j0 и выражением Vф , можно построить дисперсион- |
||||||||||||||||||
ную зависимость. Емкость и индуктивность связок определяются соотношениями, |
||||||||||||||||||
выраженными в сантиметрах (система ед. СGSE), |
|
|
|
|||||||||||||||
|
|
|
|
Ссв |
= |
(2S + d )(D - ln ) |
[см ] , |
|
|
|
||||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
ln |
|
|
- 1 |
|
|
|
|
||||
|
|
|
|
L св |
= D |
|
4 D |
|
[см ] . |
|
(1.47) |
|||||||
|
|
|
|
|
|
2 p |
|
|
|
d |
|
|
|
|
|
|
|
|
Размеры для определения С с в |
, L с в |
видны на рис 1.8 |
|
|
||||||||||||||
|
|
|
|
|
Рис 1.8 – |
Связка над сегментом. |
|
|
||||||||||
Сопротивление связи для m-ой гармоники определяется в виде |
|
|
||||||||||||||||
|
|
|
|
|
R св p |
= |
|
Z12 |
1 |
sin (0, 5b m ln ) 2 |
(1.48) |
|||||||
|
|
|
|
|
bm Z T D |
2 |
|
(0, 5bm ln ) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Соотношения для встречно штыревой и спиральной замедляющих систем |
||||||||||||||||||
приводятся в следующем разделе (примеры решения задач). |
|
|
||||||||||||||||
5.1.2. Примеры решения задач
Задача №1 (Роль углов пролета)
Расстояние между двумя плоскими электродами равно 2 мм. При каких постоянных напряжениях на электродах на частоте 3×108 Гц достигается угол пролета электронов θ = 0,33π при наличии и отсутствии пространственного заряда?
Решение
27
Угол пролета зазора при отсутствии объемного заряда, т.е. ρ = 0, и наличии, ρ ≠ 0, определяется из (1.3) и (1.7), а напряжение, соответственно, будет оп-
|
|
|
|
|
|
|
|
|
2m |
|
w2d2 |
|
2m |
|
1,52 w2d2 |
||||||
ределяться выражениями |
U0 (r=0) |
= |
|
|
× |
|
|
и U0 (r¹0) = |
|
× |
|
|
|
|
|||||||
e |
|
q |
2 |
e |
|
q |
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ОпределимU0 |
с учетом и без учета пространственного заряда: |
||||||||||||||||||||
|
2 |
|
4p×9 ×1016 ×4 ×10-6 |
|
|
|
32 ×9 |
В |
|
|
|
|
|
|
|||||||
U0 (r=0) = |
|
|
× |
|
|
|
|
|
= |
|
|
|
|
= 156 |
|
|
|
|
|
|
|
1, 76 ×10 |
|
2 |
× p |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0, 33 |
|
|
|
1, 76 ×1, 05 |
|
|
|
|
|
|
|
||||||||
U0 (r¹0) = 2, 25 ×156 = 350 В.
Вывод: Пространственный заряд как бы ослабляет поле, увеличивая время пролета. Чтобы угол пролета сделать одинаковым в случаях r = 0 и r ¹ 0 , необходимо увеличивать напряженность поля в зазоре, т.е. увеличить напряжение.
Задача №2 (Определение полного тока во внешней цепи) Конвекционный ток в пространстве между двумя электродами, к которым
приложено переменное напряжение U = 0, 4 cos wt , изменяется по закону
ik = 2 cos (wt - bx ) . Найти амплитуду полного тока во внешней цепи, если известны: размер зазора 1 мм, емкость зазора 5 пФ, рабочая частота f = 600 МГц, волновое
число b = π 103 1/м.
3
Решение При движении заряда в пространстве зазора, полный ток в его внешней це-
пи равен сумме емкостного и наведенного токов (1.10), которые определяются следующими выражениями:
iем |
= С |
dU |
= -C wU sin wt ; |
||||
|
|||||||
|
|
dt |
cos wt |
|
|
. |
|
iнав |
= M I k |
0 |
- bd |
||||
|
|
|
|
|
|
2 |
|
Найдем токи
iем |
= -5 ×10-12 ×6, 28 ×600 ×106 ×0, 4 sin wt = -7, 6 ×10-3 sin wt , A = 7, 6 ×10-3 cos p |
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
sin q |
× 2 ×10-3 ×cos wt |
|
- bd |
|
|
|
iнав |
= |
2 |
0 |
, |
||||
q |
||||||||
|
|
|
|
2 |
|
|
||
2
где t0 - время, соответствующее фазе сигнала в средине зазора.
q = |
wd |
= |
6, 28 ×600 ×106 |
×1×10-3 |
= 1, 004 радиан. |
|
|
|
|
|||||
V |
5,95 ×105 × |
|
|
|
|
|
|
|
|
|||||
0.4 |
|
|
sin (0, 5 ×q) |
|
||||||||||
|
|
|
|
|
|
|
|
|||||||
Величина М определяется из (1.13) |
M = |
= 0, 95 . |
||||||||||||
0, 5 ×q |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
iнав |
= 2 ×10-3 ×0, 25 ×cos wt0 |
|
- p |
= 1,9 ×10-3 ×cos wt0 |
- p ; |
|
||||||||
|
|
|
|
|
|
|
6 |
|
|
|
6 |
|
||
iпол |
= 1, 9 ×10-3 ×cos wt0 |
- p |
+ 7, 6 ×10-3 ×cos wt + p = |
|
||||||||||
|
|
|
|
6 |
|
|
2 |
|
|
|
||||
+ wt .
28
j |
ωt |
− |
π |
|
0 |
|
|
1,9 ×10−3 ×е |
|
|
6 |
|
ωt + |
π |
|
|
j |
|
= |
||
- 7, 6 ×10−3 ×e |
|
2 |
1, 9 |
|
|
|
|
|
|
|
|
|
|
|
×10−3 ×е |
− jπ |
− jπ |
= |
6 + 7, 6 ×10−3 ×e 2 ejωt0 |
|||
|
|
|
|
1,9 × |
cos p |
- jsin p |
+ 7, 6 × |
cos p |
- jsin p |
×10−3 |
×ejωt0 |
= (1, 65 - j0, 95) + j7, 6 ×10−3 |
×ejωt0 |
= |
||||
|
|
6 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
2 |
|
|
|
|
|
|
||
(1, 65 - j8, 55)×10−3 ×ejωt0 |
= 8, 7 ×10−3 ×ej(ωt−1,38) , А |
|
|
|
|
|
||||||||
Вывод: Полный ток представляет комплексную величину, в которой емкостная составляющая больше наведенного тока. Полный ток отстает по фазе от переменного напряжения примерно на 800 или 1,38 радиан за счет пролетных явлений в зазоре.
Задача №3(Определение предельной частоты)
Определить предельную рабочую частоту триода, в котором плотность тока эмиссии 2 А  см 2 , угол пролета зазора катод – сетка θ кс = 2 7 0 0 , размер зазора
см 2 , угол пролета зазора катод – сетка θ кс = 2 7 0 0 , размер зазора
dкс= 0,1мм.
Решение
Предельной длиной волны называется lпр , при которой прекращается рабо-
та лампы, а угол пролета в зазоре катод – сетка становится равным 3 p [3]. Эмис-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
сия с катода определяется законом “ степени |
3 |
” |
в виде |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
U3 2 |
|
|
|
U3 2 |
А |
|
|
|
|||
I = |
4 |
e0 |
2e |
× |
= 2,34 ×10 |
−6 |
× |
|
|
(1.49) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
9 |
m |
2 |
|
2 |
|
2 |
|
|
||||||||||
|
|
|
|
|
dкс |
|
|
|
dкс |
м |
|
|
|
|
|
|||
Угол пролета зазора из (1.7) записывается
q = wd |
|
|
2m |
= 6, 35 ×103 |
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.50) |
||||||||||||||||||||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
eU |
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Напряжение U не задано, но определим его из (1.50) и (1.49), найдем вели- |
|||||||||||||||||||||||||||||||||||||||||||||
чину Θ, из которой определим lпр . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
= 6,35 ×103 |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
lq |
|
|
|
|
|
|
|
|
|
|
2, 34 ×10−6 −1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
из (1.49) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I ×d2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
U |
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Id |
|
|
|
|
2, 34 ×10− |
|
|
|
|
|
|
|
|
|
|
||
|
6, 353 ×109 d3 |
= |
|
|
I ×d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
l3q3 |
|
|
2, 34 ×10−6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
6,353 ×109 ×d3 × 2, 34 ×10−6 |
|
|
|
|
|
|
6, 35 ×10 ×1, 53 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
l |
3 |
= |
или |
|
l = |
3 |
|
d |
= |
98, 6 |
3 |
|
d |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
q3 × I ×d2 |
|
|
|
|
|
|
|
|
|
|
|
q |
|
I |
q |
|
I |
||||||||||||||||||||
Рассчитаем предельную длину волны и частоту |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
lпред |
= |
98, 6 |
|
0, 01 |
= |
|
98, 6 |
|
|
= 3, 62 см |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
4, 74 |
|
2 |
|
|
4, 74 |
×5, 76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
nпр |
= |
|
с |
|
= |
3×1010 |
= 8, 6 ×109 Гц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
3, 62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
29
Вывод: На частоте 8,6 ГГц работа прибора с указанными параметрами прекращается.
Задача №4 (Определение добротностей резонатора)
Определить внешнюю, собственную и нагруженную добротности резонатора, используемого в приборе СВЧ, если на рабочей частоте 1 ГГц известно, что КПД резонатора должен быть 0,9, а степень затягивания частоты 0,5 ×107 Гц.
Решение Добротности в резонаторе связаны уравнением (1.18).
Степень затягивания частоты оценивается соотношением (1.36)
F = 0, 417 |
|
f0 |
. Коэффициент полезного действия резонатора связан с добротностя- |
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
з |
|
Qвн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ми (1.43) |
h = |
Qн |
|
= 1- |
|
Qн |
|
= |
|
Q0 |
|
|
. Внешняя добротность тогда может быть опре- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
Qвн |
|
|
|
|
|
Q0 |
|
|
|
Q0 + Qвн |
|||||||||
делена из уравнения |
|
|
|
|
Qвн |
= 0, 417 |
f0 |
. Нагруженная добротность из соотношения |
|||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fз |
||
Qн = h×Qвн = h×0, 417 × |
f0 |
|
|
.Собственная добротность из уравнения добротностей опре- |
|||||||||||||||||||||
Fз |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
деляется |
|
в виде Q0 = |
|
Qн ×Qвн |
. |
|
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qн + Qвн |
||||||||||
|
Рассчитаем требуемые по условию задачи величины |
||||||||||||||||||||||||
|
Qвн |
= 0, 417 |
109 |
|
|
|
|
|
= 208, 5 » 208 |
|
|||||||||||||||
|
0,5 ×107 |
|
|
||||||||||||||||||||||
|
Qн = 0, 9 × 208,5 = 187, 7 » 188 |
||||||||||||||||||||||||
|
Q0 |
= |
187, 7 × 208, 5 |
|
|
= |
39135, 45 |
» 1880 |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
-187, 7 + 208, 5 |
|
|
|
20,8 |
|
|
|
|
||||||||||||||
|
Q0 |
= |
Qн |
= |
187, 7 |
= 1880 |
|||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
1- h |
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задача №5 (Расчет тороидального резонатора)
Тороидальный медный резонатор используется в генераторном приборе СВЧ. Определить его резонансную частоту и предъявить требование к величине электронной проводимости, если размеры радиусов резонатора R 2 =10 мм, R1 = 5
мм, высота резонатора 10 мм, размер зазора 1 мм. Резонатор связан петлей с коаксиальной линией имеющей волновое сопротивление 50Ом, отношение площади петли связи Sn к площади сечения резонатора Sr в плоскости входа петли в резо-
натор равно 0,08.
Решение Для возбуждения генератора необходимо выполнить условие баланса ак-
тивных проводимостей (баланс амплитуд), т.е.
Gэл + G0 + Gн £ 0 .
30
