Математические основы теории систем.-2

F(λ1 ) = eλ1t = e−t = α0 − α1,

F(λ2 ) = eλ2t = e−2t = α0 − 2α1.

Решая систему уравнений, находим

α0 = 2e−t − e−2t , α1 = e−t − e−2t .

Окончательно получаем искомую функцию

Теперь что касается кратных собственных значений. Ясно, что если A имеет собственное значение λi кратности r, то подстановка λi в

уравнение (5.6.19) даст лишь одно линейно независимое уравнение. Остальные r −1 линейных уравнений для определения αi находятся дифференцированием обеих частей уравнения (5.6.19). В этом случае для нахождения единственного решения для коэффициентов αi полинома (5.6.20) нужно составить систему линейных уравнений вида

5.6.4.Теорема Сильвестра

Теорема разложения Сильвестра находит применение при отыскании матричных функций, представляющих в замкнутой форме степенные ряды матрицы А.

Теорема 5.6.2 (Сильвестра). Пусть N(A) – матричный многочлен от

A (неважно, конечный или бесконечный) и квадратная матрица A имеет n различных собственных значений. Тогда имеет место формула

275

где D(λ) – характеристический полином A .

С учетом соотношения (5.6.25) формула (5.6.24) примет вид

При наличии у A кратных собственных значений формула (5.6.26) нуждается в модификации. Можно показать, что составляющая N(A) ,

обусловленная собственным числом λi кратности r, равна

Очевидно, что формула (5.6.27) годится и для простых корней (r = 1) , поэтому окончательно

где суммирование производится по всем различным корням, причем кратные корни входят в сумму (5.6.28) только один раз.

Уравнение (5.6.28) носит название вырожденной формы теоремы Сильвестра.

Контрольные вопросы

1.Дайте определение матрицы.

2.Перечислите операции над матрицами.

277

3.Что такое определитель матрицы?

4.Чем отличается минор от алгебраического дополнения?

5.Назовите виды матриц.

6.Что такое дефект матрицы и как он связан с рангом?

7.Для каких матриц не существует обратных?

8.Что такое след матрицы?

9.Что такое ортогональные векторы?

10.Дайте определение базиса.

11.Что такое сопряженный базис?

12.В чем заключается процедура ортогонализации Грама – Шмидта?

13.Что такое собственные числа и собственные векторы квадратной матрицы А?

14.Как строится модальная матрица, соответствующая матрице А?

15.Что такое эквивалентные матрицы?

16.Как выглядит преобразование подобия?

17.Любую ли матрицу можно привести к диагональному виду?

18.В чем заключается необходимое и достаточное условие положительной определенности квадратичных форм?

19.Существуют ли дробные степени от матриц?

20.Сформулируйте теорему Кэли – Гамильтона.

21.Для чего можно использовать теорему Кэли – Гамильтона?

22.Какие методы используют для вычисления матричных функций?

278

6. ВЕКТОРНО-МАТРИЧНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

6.1 Уравнения состояния

Альтернативной дифференциальному уравнению n-го порядка формой описания динамических систем является векторно-матричная форма. Векторно-матричная форма по сути является записью дифференциального уравнения n-го порядка в нормальной форме Коши с привлечением дополнительных переменных, называемых переменными состояния.

Определение переменных состояния уже давалось в подразделе 1.3.5, но нелишне вспомнить его ещё раз. Переменные состояния системы – это такие переменные, знание значений которых в некоторый начальный момент времени t0 позволяет определить поведение системы в текущий момент

времени t > t0 (естественно, если известны входные воздействия системы на интервале (t0 ,t) ). Если ввести обозначения r(t) – входные переменные,

у(t) – выходные переменные, x(t) – переменные состояния, то общее математическое описание динамической системы задается уравнениями

x(t) = δ(x(t0 ),r(τ)), (6.1.1)

y (t) = λ (x(t0 ),r(τ)),

где δ и λ являются однозначными функциями, а τ – отрезок оси времени от t0 до t.

Уравнения (6.1.1) называются уравнениями состояния. Часто уравнением состояния называется первое из уравнений (6.1.1), а второе носит название уравнения выхода.

6.2 Обыкновенные дифференциальные уравнения

Если динамическая система описывается или может быть описана обыкновенным линейным дифференциальным уравнением n-го порядка, то переход к нормальной форме Коши дает уравнения состояния такой системы. Переход от дифференциального уравнения к уравнениям состояния может быть произведен различными способами в соответствии с различным определением переменных состояния, важно только, чтобы переменные состояния системы подлежали измерению (контролю).

279

Например, перейти от дифференциального уравнения к уравнениям состояния можно следующим образом. Пусть (для простоты) в дифференциальном уравнении отсутствуют производные входного воздействия. Так же, не снижая общности можно положить коэффициент при старшей производной единице. Тогда дифференциальное уравнение имеет вид

...

xn = xɺn−1 = y(n−1).

Подставив значения y и его производных в уравнение (6.2.1), найдем

dxdtn = xɺn = −an x1 − an−1x2 −...− a1xn + r .

Полученные уравнения запишем в нормальной форме Коши, то есть первые производные перенесем в левую часть, а все остальное – в правую. В результате получим систему уравнений

xɺ1 = x2 , xɺ2 = x3,

...

(6.2.2)

xɺn−1 = xn ,

xɺn = −an x1 − an−1x2 − a1xn + r, y = x1.

Уравнения состояния (6.2.2) удобнее записать в матричной форме

280

Уравнения состояния (6.2.3) с матрицами вида (6.2.4) носят название стандартной формы (у некоторых авторов можно встретить название

каноническая форма фазовой переменной). Матрица А вида (6.2.4) называется матрицей Фробениуса.

Уравнения (6.2.3) естественным образом обобщаются на случай многомерной системы, имеющей m входов и р выходов. Тогда в общем виде r и у являются векторами и, кроме того, выход может напрямую зависеть от входа. С учетом этого общий вид уравнений состояния будет такой

•

x = A(t)x + B(t)r, (6.2.5) y = C(t)x + D(t)r,

где A(t),B(t),C(t) и D(t) – матрицы соответствующих размерностей с

изменяющимися в общем случае во времени элементами.

Блок-схема системы, соответствующая уравнениям (6.2.5), приведена на рис. 6.1.

D(t)

A(t)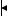

Рис. 6.1. Блок-схема уравнений состояния.

281

Для системы с постоянными параметрами матрицы A(t),B(t),C(t), D(t) от времени не зависят и могут записываться просто как A,B,C,D . В случае стационарных систем уравнения состояния записываются, таким образом, как

y= Cx + Dr.

6.3Каноническая форма

При исследовании систем, описываемых уравнениями состояния, часто является удобным такой выбор переменных состояния, чтобы разноименные компоненты вектора состояния не зависели друг от друга.

Возьмем уравнения состояния (6.2.6), где, в общем случае, матрица A

– произвольная квадратная матрица с различными собственными значениями. Произведем линейное преобразование x = Mq , где M – модаль-

ная матрица. Тогда уравнения (6.2.6) запишутся в виде

Так как матрица M является модальной матрицей, преобразование подобия M−1AM дает диагональную матрицу Λ с собственными числами λ1,λ2 ,...,λn по диагонали. Окончательно имеем

Уравнения (6.3.2) носят название нормальной или канонической формы уравнений состояния. При этом дифференциальные уравнения развязаны относительно переменных состояния q1,q2 ,...,qn и имеют вид

•

qi = λi qi + fi , где fi – вынуждающая функция, воздействующая на i-ю

переменную состояния.

Можно показать, что, если уравнения (6.2.6) представлены в стандартной форме (т.е. матрица A является матрицей Фробениуса), то модальная матрица M имеет вид

Матрица вида (6.3.3) называется матрицей Вандермонда.

При наличии у A кратных собственных значений и в случае, когда дефект характеристической матрицы [λiE− A] меньше кратности корня

λi , диагональная матрица Λ в уравнении (6.3.2) заменяется недиагональной матрицей Жордана.

6.4Обыкновенные уравнения стационарных систем

6.4.1.Переходная матрица и методы ее вычисления

Однородное уравнение для линейной стационарной системы имеет вид

где A – квадратная размерностью n матрица с постоянными коэффициентами, х – вектор-столбец переменных состояния. Аналогично скалярному случаю, общее решение уравнения (6.4.1) ищется в виде

где матрица eA(t−t0 ) определяется уравнением (5.6.6), а вектор x(t0 ) зада-

ет начальные условия.

Подставив выражение (6.4.2) в уравнение (6.4.1) и выполнив дифференцирование по всем правилам, удостоверимся, что оно (выражение (6.4.2)) действительно является решением однородного дифференциального уравнения. Подставив в формулу (6.4.2) t = t0 , можно убедиться, что

Матрица Φ(t − t0 ) = eA(t−t0 ) , удовлетворяющая однородному диффе-

ренциальному векторно-матричному уравнению (6.4.1), называется переходной матрицей или фундаментальной матрицей. Термином «фундаментальная матрица» чаще пользуются математики, связанные с матричными дифференциальными уравнениями, а словосочетание «переходная матрица состояния» встречается в теории управления и теории систем. Прилагательное «переходная» обусловлено тем, что с помощью матрицы Φ(t − t0 ) осуществляется «переход» системы от некоторого начального

состояния x(t0 ) к текущему состоянию x(t) . Часто для простоты начальный отсчет времени полагают равным нулю t0 = 0 .

Для вычисления переходной матрицы Φ(t) могут применяться не-

сколько методов. Из уже рассмотренных методов сюда относятся методы, основанные на теореме Кэли – Гамильтона и теореме разложения Сильвестра (см. примеры 5.9 и 5.10).

К другим методам относятся метод разложения в степенной ряд и метод, основанный на преобразовании Лапласа.

Метод разложения в степенной ряд. Согласно уравнению (5.6.6) переходную матрицу Φ(t) можно представить бесконечным рядом

Вычисление ряда (6.4.3) – задача трудоемкая, особенно если ряд сходится медленно, а порядок матрицы Φ(t) недостаточно низкий. Степени

матрицы Ak могут быть найдены с использованием теоремы Кэли – Гамильтона. После выполнения суммирования необходимо найти в замкнутом виде все элементы матрицы Φ(t) . Количество членов при вычисле-

нии ряда (6.4.3) определяется скоростью сходимости: ограничиваются

284