Вакуумная и плазменная электроника.-7

а выражение (5.76) совпадает с выражением (5.75).

Отвечающая этому равновесию степень ионизации определяется соотношением

где p = (ne ni na )T – давление, определяемое всеми частицами

в объеме. Выражение (5.77) представляет собой формулу Саха. Она имеет большое значение и связывает основные фундаментальные характеристики взаимодействующих частиц. Формула Саха справедлива, если ионизация и рекомбинация происходят по одному и тому же пути и плазму можно рассматривать как идеальный газ.

5.1.9 Излучение плазмы

Плазма по составу представляет собой сложную систему, которая включает в себя частицы разного сорта, взаимодействующие друг с другом. В частности, результатом взаимодействия частиц является излучение света, т.е. испускание фотонов. Излучение света может быть одним из основных каналов потерь энергии из плазмы. Существенные потери энергии плазмы на излучение влияют на ее энергетический баланс, температуру и на протекание разрядного процесса, формирующего плазму. Кванты света появляются и исчезают при радиационных переходах электронов из одних энергетических состояний в другие. Плотная равновесная плазма является более мощным излучателем, чем слабоионизованная. В отличие от последней взаимодействие электронов с ионами играет в ней очень большую роль, в том числе и в отношении излучения. Что касается электронно-электронных

151

столкновений, то ни излучения, ни поглощения света при этом не происходит. Преобладающими процессами плазмы, которые сопровождаются излучением, являются тормозное, рекомбинационное излучения и излучение резонансной полосы (таблица 5.4).

Таблица 5.4 – Процессы в плазме, сопровождающиеся излучением

Рассмотрим систему, которая состоит из положительного иона и электрона. Схема энергетических уровней электрона для рассматриваемого случая представлена на рисунке 5.4.

E

Свободно-свободные

Связанно-свободные

Связанно-связанные

Рисунок 5.4 – Схема энергетических уровней и переходов электрона в поле положительного иона

Энергия отсчитывается от границы непрерывного спектра, разделяющей свободные и связанные состояния. Уровни связанных состояний к границе сгущаются. Нижний уровень соответствует основному состоянию атома. Стрелками показаны возможные типы переходов: свободно-свободные, связанно-свободные,

152

связанно-связанные. Переходы сверху вниз сопровождаются излучением кванта энергии hν, равной разности между энергиями верхнего и нижнего состояний; переходы снизу вверх – поглощением.

Свободно-свободные переходы представляют собой тормозное излучение при кулоновских столкновениях электронов с ионами и обратные процессы тормозного поглощения. Связанносвободные переходы – это процессы фотоионизации и фотозахвата. Свободно-свободные и связанно-свободные переходы дают непрерывные спектры, поскольку либо начальное, либо конечное, либо оба этих состояния электрона лежат в непрерывном энергетическом спектре. Связанно-связанные переходы электрона между дискретными уровнями в атоме приводят к излучению и поглощению спектральных линий. Разновидностью линейчатых спектров являются полосатые спектры молекул, которые также обязаны своим происхождением связанно-связанным переходам. Насыщенность молекулярных спектров линиями, которые внутри полосы располагаются очень тесно, обусловлена сложностью системы энергетических уровней молекулы. Каждому электронному состоянию соответствует множество колебательных и вращательных состояний, и возможно много вариантов переходов между ними.

Свободно-свободные и связанно-свободные переходы происходят и при взаимодействии электронов с нейтральными атомами. Тормозное поглощение такого рола является главным механизмом диссипации энергии электромагнитных волн и внешних излучений в слабоионизованном газе. Тормозное излучение в оптическом диапазоне в слабоионизованном газе является крайне слабым из-за малости числа электронов. В качестве механизмов излучения и поглощения света роль связанно-свободных переходов в газоразрядной плазме не очень значительна.

С необходимыми общими понятиями теории излучения – интенсивность излучения, вынужденное и спонтанное испускание, коэффициент поглощения света, закон Кирхгофа, выражающий принцип детального равновесия для излучения, и др. – можно ознакомиться в [4].

153

Рассмотрим тормозное излучение при столкновениях электронов с ионами. Тормозное излучение обусловлено неравномерным движением электронов в полях ионов (столкновениями электронов с ионами), которые приближенно можно считать неподвижными. Спектр тормозного излучения является непрерывным (сплошным) и лежит в области высоких частот порядкаторм 2 T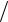h , поскольку при торможении электрон может терять

от нулевой до максимальной энергии. Это соответствует низкоэнергетическому рентгеновскому излучению, и для таких частот плазма фактически прозрачна, поэтому тормозное излучение свободно выходит наружу. Дифференциальное сечение тормозного излучения

где d – нормированная на единицу функция максвелловского распределения электронов; min 2 / me – наименьшая

скорость, имея которую электрон может испускать квант энергии. Спектр тормозного излучения определяется экспоненциаль-

ным множителем exp kT . В основном излучаются кван-

ты энергии порядка kT. Квантов с энергией kT излучается мало: их способны испускать только очень энергичные электроны, принадлежащие «хвосту» максвелловского распределения.

154

Общая интенсивность тормозного излучения Qd определяется

концентрациями электронов и ионов с учетом их зарядности Z, поскольку излучение тем сильнее, чем больше электрические поля:

где b1 – постоянная.

Теперь рассмотрим рекомбинационное излучение плазмы. Оно возникает при захвате ионом приближающегося к нему электрона. В процессе захвата электрона на скорости в связанное состояние с отрицательной энергией En излучается квант энергии

Для данного процесса оценочное значение сечения захвата для водородоподобной системы можно найти по выражению [4]

где n – главное квантовое число. При этом энергия En определяется выражением

В результате радиационного захвата электронов со скоростями от до + d на Nq-й уровень атомов в 1 см3 за 1 с излучается энергия

Кванты определенной энергии могут излучаться при захвате электрона на самые различные уровни, однако его энергия

155

должна иметь избранные значения, регламентируемые равенством (5.81). Поэтому, интересуясь излучательной способностью газа в данном спектральном интервале, выражение (5.84) следует просуммировать по всем тем уровням, захват на которые может привести к излучению кванта данной энергии. В излучении квантовE1 (n = 1) могут участвовать все уровни от n = 1 до ∞. Излу-

чить же квант с энергией E1 электрон может только при за-

хвате на достаточно высокие уровни с n n* . Самый нижний из них ( n*-й) определяется условием En* En* 1 . Таким обра-

зом, в результате всех возможных радиационных захватов в 1 см3 за 1 с в интервал d излучается энергия

J rec d d J n . (5.85) n*

Поскольку распределение электронов по скоростям описывается статистикой Максвелла – Больцмана и, следовательно, скорости электронов могут принимать любые значения, то и в этом случае спектр излучения будет непрерывным. Общую интенсивность рекомбинационного излучения Qrec можно определить по выра-

жению

где b2 – константа.

5.2 Плазма в магнитном поле

Плазма под действием магнитного поля теряет изотропию, многие ее свойства и параметры значительно изменяются. Например, используя магнитное поле, можно создавать плазменные конфигурации, которые занимают ограниченную часть пространства, что совершенно не свойственно обычному газу.

При рассмотрении плазмы в магнитном поле будем пользоваться одночастичным приближением (или рассмотрением) процессов, происходящих в ней. Данный подход заключается в том, что описание плазменных процессов сводится к изучению движе-

156

ния отдельных частиц плазмы в полях, которые считаются заданными изначально. Тем самым не учитывается влияние движения частиц плазмы на поля, «управляющие» их движением, т. е. пренебрегается эффектами самосогласования движения частиц и вызываемого им изменения поля. Одночастичное приближение в качестве первого шага вполне оправдано и повсеместно используется, особенно если есть возможность, по крайней мере, эффективно учесть влияние полей остальных частиц плазмы на движение какой-либо одной выделенной частицы.

В общем случае уравнение движения частицы с зарядом q и

где E – напряженность электрического поля; B – индукция магнитного поля; первое слагаемое отвечает силе со стороны электрического поля, второе описывает силу со стороны магнитного поля (сила Лоренца), а третье слагаемое (F) обозначает равнодействующую прочих внешних сил, которые могут действовать на частицу.

5.2.1Движение заряженной частицы в постоянном

иоднородном магнитном поле

Рассмотрим движение заряженной частице в постоянном и однородном магнитном поле в случае, когда других сил, кроме силы Лоренца, нет. Тогда выражение (5.87) будет иметь вид

Умножая скалярно правую и левую части выражения (5.88) на скорость и учитывая, что сила Лоренца перпендикулярна к обоим векторам, входящим в векторное произведение (5.88), получим соотношение

Отсюда следует, что кинетическая энергия частицы сохраняется:

157

производит работы над заряженной частицей. Поэтому модуль скорости этой частицы, заданный начальными условиями, сохраняет постоянное значение.

Разложив вектор скорости на компонент, параллельный магнитному полю, и компонент, перпендикулярный к магнитному

Следовательно, постоянное и однородное магнитное поле не меняет продольный компонент скорости, а B B const .

Из выражения (5.94) следует, что поперечный компонент меняется только по направлению. Следовательно, заряженная частица равномерно движется вдоль силовой линии поля, вращаясь при этом вокруг силовой линии по окружности с постоянной угловой скоростью.

Таким образом, если плазму поместить в постоянное и однородное магнитное поле, то заряженные частицы, в первую очередь электроны, будут вращаться по некоторым круговым орбитам ра-

158

Радиус rB , определяемый выражением (5.95), называют ларморовским радиусом частицы, а угловую скорость B , опреде-

ляемую (5.96), – ларморовской или циклотронной частотой. Из выражений (5.95) и (5.96) видно, что ларморовский радиус зависит от составляющей скорости, перпендикулярной к магнитному полю, причем с ее увеличением радиус возрастает прямо пропорционально, а циклотронная частота зависит от массы и заряда частицы, напряженности магнитного поля, но не зависит от величины скорости вращающейся в поле частицы. Следует отметить, что вектор угловой скорости положительно заряженной частицы антипараллелен, а отрицательно заряженной частицы (например, электрона) – параллелен магнитному полю. Поскольку движению заряженной частицы по окружности можно уподобить круговой ток I q 2 , то вращению частицы в магнитном поле можно

сопоставить магнитный момент Mm , равный магнитному моменту этого кругового тока:

где S – соответственно ориентированная площадь круга, охватываемая ларморовской окружностью радиусом rB .

Магнитный момент вращающейся в магнитном поле частицы всегда направлен против этого поля, следовательно, положительно и отрицательно заряженные частицы вращаются в противоположных направлениях. В общем случае траектория движения частицы в постоянном и однородном магнитном поле представляет собой спираль.

5.2.2Движение заряженной частицы

всильном медленно меняющемся поле. Дрейфовое приближение

Рассмотрим случай движения заряженной частицы в сильном медленно меняющемся магнитном поле. Когда магнитное поле медленно меняется в пространстве и во времени, то движущаяся в нем заряженная частица, прежде чем почувствует влияние

159

изменения поля, совершит в нем множество ларморовских оборотов, навиваясь на силовую линию магнитного поля. Движение заряженной частицы по ларморовскому радиусу было рассмотрено в ранее. Проанализируем движение не собственно заряженной частицы, а ее мгновенного центра вращения, так называемого ведущего центра. В случае если магнитное поле меняется во времени, то необходимо учитывать слабые электрические поля. Согласно уравнениям Максвелла в силу

переменное во времени магнитное поле вызывает появление вихревого электрического поля.

На медленное движение ведущего центра, определяемого как продольной скоростью частицы, так и влиянием слабого электрического поля и слабых неоднородностей магнитного поля, накладывается быстрое вращение частицы вокруг силовых линий магнитного поля. Такое раздельное рассмотрение быстрого вращения частицы по ларморовской окружности и медленного «дрейфа» центра этой окружности будет справедливо, если изменение ларморовского радиуса на одном обороте будет существенно меньше самого ларморовского радиуса. Это условие будет выполнено, если характерное время t f изменения полей будет значительно

больше времени ларморовского оборота tL ( t f tL ) и если характерный пространственный масштаб изменения полей l f будет значительно превышать ларморовский радиус rB ( l f rB ).

Количественно данные критерии можно представить следующим образом:

Условия, описываемые выражениями (5.99), выполняются тем лучше, чем больше величина индукции (напряженности) магнит-

160