Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Основы физической и квантовой оптики.-1

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

535.59 Кб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

В.М. Шандаров

ОСНОВЫ ФИЗИЧЕСКОЙ И КВАНТОВОЙ ОПТИКИ

Сборник задач для студентов специальности 210401 – Физика и техника оптической связи

Учебно-методическое пособие

Томск

ТУСУР

2012

УДК 621.37. (075.8+537.8(0758)

Рецензент:
Зав. каф. СВЧиКР, профессор	Шарангович С.Н.

Шандаров В.М.

Основы физической и квантовой оптики. Сборник задач для студентов очной и заочной форм обучения: Учебно-методическое пособие. – Томск:

ТУСУР, 2012. – 59 с.

Учебно-методическое пособие включает краткое изложение основных положений, определений и соотношений физической и квантовой оптики. Приведены примеры решения стандартных задач. Представлен набор задач для самостоятельного решения.

Для студентов очной и заочной форм обучения специальности 210401 – «Физика и техника оптической связи» по дисциплине «Основы физической и квантовой оптики».

УДК 621.37. (075.8+537.8(0758)

©Томск. гос. ун-т систем управления и

радиоэлектроники,	2012
© Шандаров В.М.	2012

Оглавление
1. ПЛОСКИЕ СВЕТОВЫЕ ВОЛНЫ………………………………….	4
Волновые уравнения для безграничной среды …………………..	4
Решение волнового уравнения - плоские волны ..……………….	4
Гармонические плоские волны ……………………………….…..	5
Распространение плоской волны в произвольном
направлении …………………………………………………...	6
Поляризация плоских световых волн ………………………….…	6
Поляризаторы ……………………………………………………...	9
Фазовые пластинки …………………………………………….….	10
Примеры решения задач ……………………………………….….	11
Задачи для самостоятельного решения ……………………….….	13
2. ДИФРАКЦИЯ СВЕТА НА ЩЕЛИ И ПЕРИОДИЧЕСКИХ
СТРУКТУРАХ ………………….	17
Примеры решения задач ……………………………………..….	18
Задачи для самостоятельного решения ……………………..….	20
3. ГАУССОВЫ СВЕТОВЫЕ ПУЧКИ ……………………………...	22
Примеры решения задач ……………………….……………….	23
Задачи для самостоятельного решения ………….…………….	24
4. РАСПРОСТРАНЕНИЕ СВЕТА В НАПРАВЛЯЮЩИХ
СТРУКТРАХ ………………………………………………………...	26
Примеры решения задач …………………………………….….	28
Задачи для самостоятельного решения …………………….….	29
5. ВЗАИМОДЕЙСТВИЯ СВЕТА С ФИЗИЧЕСКИМИ ПОЛЯМИ..	32
Примеры решения задач …………………….……………….	53
Задачи для самостоятельного решения ……………………….	54
Список литературы …………………………………………………..	58

1. ПЛОСКИЕ СВЕТОВЫЕ ВОЛНЫ

Волновые уравнения для безграничной среды

Решения для световых волн в диэлектрической безграничной однородной изотропной среде вытекают из уравнений Максвелла в дифференциальной форме при отсутствии в среде сторонних токов и зарядов. Для векторов напряженностей электрического и магнитного полей E и H эти уравнения в системе СИ принимают вид [1]:

		= ε ∂
				E		(1.1а),
rotH
			∂t
				∂
	= −μ				H	(1.1б),
rotE
				∂t
			= 0			(1.1в),
divE
		= 0				(1.1г),
divH

где ε и μ - абсолютные диэлектрическая и магнитная проницаемости среды. Используя стандартную методику, из (1.1 б и 1.1 а) можно получить волновые уравнения для векторов E и H :

				¶2
Ñ2			- me		E		= 0	(1.2).
Ñ2		E	- me		E		= 0	(1.2).
				¶t 2
				¶2
2						H
2	H - me					H	= 0	(1.3).
Ñ	H - me			¶t 2			= 0	(1.3).
				¶t 2

Решение волнового уравнения - плоские волны

В предположении зависимости поля E координаты z, уравнение (1.2) принимает вид:

¶2			¶2
	E	- em		E	= 0
¶z 2			¶t 2

лишь от пространственной

(1.4).

С учетом условия divD = 0 , световое возмущение - решение волнового уравнения (1.2) может иметь только поперечную (относительно направления распространения) компоненту поля E .

Пусть Ey=0, а Ex ¹ 0 , тогда (1.4) имеет вид скалярного одномерного волнового уравнения:

¶2 E	x - me	¶2 E	x	= 0	(1.5).
¶z 2		¶t 2

Его решение представляется в виде плоских скалярных волн:

(t, z) = Ex1

(t -

) + Ex 2

(t +

)

(1.6).

Здесь v =

- скорость распространения волны в среде,

а первое и

второе слагаемые соответствуют волнам, бегущим в направлениях +z и – z.

Но

м× е = м × е × м × е .

Тогда

v =

где

m =

m0 × e0

× mr

× er n

er =

- относительные

магнитная и диэлектрическая

проницаемости

n =

среды;

× er

ее

показатель

преломления.

Постоянные

м = 4р ×10−7 Гн/м ;

е =

×10−9 Ф/м ; c = 3 ×108

м/с [2, 3].

36p

Гармонические плоские волны

Если при z=0 задано возмущение вида

E(t) = Em × cos(wt + j) ,

то,

согласно (1.6):

E (z,t) = E

× cos[w(t -

) + j]

(1.7),

E2 (z,t) = Em2

× cos[w(t +

) + j]

т.е. ему соответствуют две гармонические плоские волны, бегущие в направлениях +z и – z. Мгновенное значение возмущения в некоторой точке определяется амплитудой Em волны и ее фазой


[w(t M	z	) + j] =[wt M k × z + j], где			k = ω - волновое число. Если Em не

	v				v
зависит от поперечных координат, то волна называется однородной.
Геометрическое				место	точек, в которых фаза волны
( wt M kz + j = const )			одинакова,		называется волновым или фазовым
фронтом.				t=t0 фаза плоской волны (wt M kz + j) = const при
В момент времени
некотором значении			z,	то есть	волновой фронт является плоскостью,

нормальной к оси z. Отсюда и термин «плоская волна. За время Dt волновой фронт смещается в пространстве на расстояние Dz . При этом (w × Dt - k × Dz) = 0 , так как фаза волны определяется выбранным волновым

фронтом. Отсюда:

ω =	z = vф	(1.8),
k	Dt
где vф - фазовая скорость волны.		В пространстве изменение ее фазы
Dj = 2p соответствует расстоянию,		равному длине волны l . Поскольку

Dj = k × l = 2p , то k = 2lπ .

Распространение плоской волны в произвольном направлении

При распространении плоской волны в произвольном направлении, не совпадающем с какой – либо координатной осью декартовой системы, поле гармонической плоской волны может быть записано в виде:

E(
		,t) = Em × cos(wt - k		×		)	(1.9).
	r				r
			- волновой вектор, параллельный
Здесь полагается, что j = 0 , а вектор k

единичному вектору нормали к фазовому фронту n . Величина и

определяются соотношением:

направление вектора k

× =

× w × me = (

0 nx +

0 ny +

0 nz ) ,

где nx, ny и nz – декартовы координаты единичного вектора n . Вектор k в этой системе координат имеет вид: k = k (x0 cosα + y0 cos β + z0 cos γ ) , где

a, b, g - углы между единичным вектором нормали к волновому фронту волны и осями x, y, z. Тогда:

			×		= k (x × cosα + y × cos β + z × cosγ )	(1.10).
		k
				r
В результате получаем:
E(		, t) = Em × cos[ωt - k (x × cosα + y × cos β + z × cos γ )]				(1.11).
	r

Поляризация плоских световых волн

Световая волна с векторами E и H , направление которых может быть однозначно определено в любой момент времени в любой точке пространства, называется поляризованной [1 - 3].

При случайных положениях векторов E и H в пространстве световое поле является неполяризованным.

Плоскость поляризации – это плоскость, в которой лежат вектор E и вектор k . В зависимости от того, какую фигуру описывает конец вектора E в пространстве при распространении световой волны, различают

линейную, круговую и эллиптическую поляризации.

Математически волну с произвольной поляризацией, бегущую вдоль оси OZ, можно представить в виде двух составляющих:


		x =				0 E1m cos(wt - kz)		(1.12 а),
E
				x
			y =				0 E2m cos(wt - kz - j)	(1.12 б).
	E
					y

В общем случае эти составляющие в плоскости, ортогональной волновому вектору, имеют разные амплитуды и сдвинуты по фазе друг относительно друга. Для плоскости z=0 эти выражения принимают вид:

Исключив из соотношениям, плоскости XOY:

		Ex	2
		Ex


		E1m

= cos(wt)

(1.13),

E1m

= cos(wt) × cos j + sin(wt) × sin j

(1.14).

E2m

данных уравнений временной множитель, придем

описывающим

изменение

положения вектора

- 2

× cos j = sin j

(1.15).

E2m

E1m

E2m

Характерные виды поляризации плоской волны соответствуют различным фазовым сдвигам ϕ :

1. ϕ = 0 .

В этом случае:

E	x	=	Ey	®	Ey =	E	2m	Ex	(1.16).
E1m			E2m
						E1m

Это уравнение прямой с наклоном к оси OX, определяемым отношением

E2m	.	Очевидно,	что	поляризация	будет	линейной	при

E1m
j = np,		(n = 0,±1,......) .	Поле плоской волны с линейной поляризацией в

общем случае можно записать в форме:

E = (x0 E1m + y0 E2m ) cos(ωt − kz) = E0 (x0 cos α + y0 sin α) cos(ωt − kz) (1.17),

где α = arctg(E2m / E1m ) . В частных случаях, при поляризации света в плоскостях XOZ и YOZ получим, соответственно: E = E0 x0 × cos(wt - kz) ,

E = E0 y0 × cos(wt - kz) .

2. ϕ = 90° .

При этом из (1.15):

E	x	2		Ey	2
	x					= 1	(1.18).

			+
E1m				E2m

Это уравнение эллипса с большой и малой полуосями, ориентированными по осям x и y. Направление вращения вектора E определяется знаком j.


При	j=90º	из	(1.12)	следует:	Ex	= E0 cos(ωt) ,		а
Ey = E0 cos(ωt − 90°) = E0 sin(ωt) .				Вращение вектора			в этом случае
Ey = E0 cos(ωt − 90°) = E0 sin(ωt) .				Вращение вектора		E	в этом случае

происходит по часовой стрелке, если смотреть вдоль направления распространения волны. Такую поляризацию называют левой эллиптической поляризацией. Для фазового сдвига ϕ = −90° вектор E вращается в противоположном направлении – это правое вращение. Если выполняется условие E1m=E2m, то эллипс превращается в окружность, а поляризацию называют круговой. В этом случае поле плоской волны может быть записано в виде:

= E0[

0 cos(wt - kz) +

0 sin(wt - kz)]

(1.19).

Или, при использовании комплексной формы записи:

(1.20).

E = E0 (x0 ± +iy0 ) × exp[i(wt - kz)]

Волна с круговой поляризацией представляется суммой двух линейно поляризованных волн с одинаковыми частотами и фазовым сдвигом (p/2±mp). В свою очередь, линейно поляризованная волна может быть представлена в виде суммы волн правой и левой круговой поляризации. Действительно, взяв для определенности волну с линейной поляризацией в плоскости XOZ, представим ее поле в виде:

E = E0 x0 exp[i(wt - kz)] =

[(x0

+ iy0 ) + (x0

- iy0 )]exp[i(wt - kz)] =

(1.21).

(

0 + iy

0 ) exp[i(wt - kz)] +

(

0 - iy

0 ) exp[i(wt - kz)]

3. Произвольный фазовый сдвиг j. В этом случае поляризация световых волн также эллиптическая, но направления главных осей эллипса поляризации не совпадают с координатными осями X и Y. Эллипс вписан в прямоугольник с размерами сторон 2Em1 и 2Em2 (рис. 1.1). Угол Ψ между

Em1,

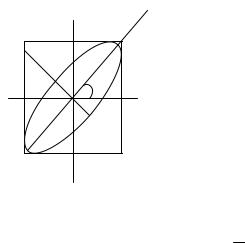
Рис. 1. 1. Ориентация эллипса поляризации при произвольном φ.

Поляризаторы

направлением главной оси эллипса поляризации и осью X можно выразить через амплитуды компонент Em2 и фазовый сдвиг j следующим образом [1, 2]:

tg 2y =	2E1m E2m		× cosj	(1.22).

	E 2	- E 2
	1m	2m

Поле плоской световой волны, бегущей в

направлении оси OZ, при эллиптической поляризации, можно записать в виде:

	&
	&	+ y0 E2m exp(-ij)] × cxp[i(wt - kz)]
E = [x0 E1m		+ y0 E2m exp(-ij)] × cxp[i(wt - kz)]
		(1.23).

Поляризаторы - это элементы, преобразующие состояние поляризации световых волн. Они используют эффекты оптического дихроизма (анизотропии поглощения света) и оптической анизотропии кристаллических материалов [1 - 4].

Дихроичные поляризаторы имеют в основе полимерные пленки с молекулами в виде длинных цепочек, ориентированных преимущественно

водном направлении. Пример - пленки поливинилового спирта с добавками йода или хинина. Они могут пропускать до 80% света, поляризованного в одном направлении, и менее 1% света, поляризованного

вортогональном направлении. Достоинство таких поляризаторов – низкая цена, основной недостаток – низкая лучевая стойкость.

Кристаллические поляризаторы изготавливаются, как правило, из

природного или синтетеического исландского шпата (кальцит, CaCO3). Они обладают высоким оптическим качеством, прозрачны в диапазоне длин волн от 0,2 до 2,2 мкм, устойчивы к воздействию интенсивного лазерного излучения. Существует несколько типов таких элементов. Это призмы Николя, Глана, Волластона, Рошона и т.д. Призмы Николя и Глана пропускают излучение лишь одной поляризации, призмы Волластона и Рошона на выходе имеют два ортогонально поляризованных световых луча, распространяющихся под некоторым углом относительно направления падающего излучения.

Интенсивность света при прохождении линейно поляризованной волны через поляризатор определяется законом Малюса:

Iвых = I0 × cos2 θ	(1.24),
где I0 - интенсивность падающей световой волны,	θ - угол между

направлением поляризации света и главным направлением поляризатора.

Фазовые пластинки

Фазовые пластинки преобразуют линейно поляризованный свет в свет с эллиптической (круговой) поляризацией и наоборот [1 - 3]. Это плоскопараллельные образцы с толщиной d, вырезанные из одноосного кристалла, с оптической осью, лежащей в плоскости пластинки. Линейно поляризованная плоская световая волна с вектором E , отклоненным от оптической оси на угол в 45°, в пластинке распадается на обыкновенную и необыкновенную волны, распространяющиеся в кристалле со скоростями

vo = c / no и ve = c / ne . Разность			фаз	между обыкновенным и
необыкновенным лучами на выходе пластинки толщиной d:
Φ =	2π	(n	− n )d	(1.25).
	λ
		0	e

Поляризация прошедшего через пластинку светового поля определяется величиной Φ . На практике стандартными элементами являются четвертьволновые (λ/4) и полуволновые (λ/2) пластинки. Для λ/4 пластинки Φ =π/2 и при линейной поляризации падающей световой волны прошедшая через пластинку будет иметь круговую поляризацию. Для полуволновой пластинки Φ =π и при линейной поляризации падающей волны прошедшая волна остается также линейно поляризованной, но плоскость ее поляризации поворачивается на 90°.

Очевидно, что если падающая на полуволновую пластинку световая волна имеет круговую поляризацию, то пластинка меняет на противоположное направление вращения вектора E в прошедшей волне. В подобной ситуации четвертьволновая пластинка преобразует свет с круговой поляризацией в линейно поляризованный.

При заданной толщине пластинки фазовый сдвиг между волнами с ортогональной поляризацией может быть равен π или π/2 только на определенной длине волны.

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023186.9 Кб1Основы управленческой деятельности.-6.pdf
#
05.02.20231.17 Mб2Основы управленческой деятельности.-7.pdf
#
05.02.2023594.86 Кб1Основы управленческой деятельности..pdf
#
05.02.20231.96 Mб33Основы физики горения и взрыва..pdf
#
05.02.2023408.84 Кб5Основы физики твердого тела..pdf
#
05.02.2023535.59 Кб2Основы физической и квантовой оптики.-1.pdf
#
05.02.2023534.27 Кб7Основы физической и квантовой оптики.-2.pdf
#
05.02.20233.95 Mб5Основы физической и квантовой оптики..pdf
#
05.02.2023542.55 Кб19Основы физической оптики.-1.pdf
#
05.02.20231.96 Mб8Основы физической оптики..pdf
#
05.02.202353.19 Кб0Основы физической подготовки гребцов..pdf