Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Антенны и устройства СВЧ.-2

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2.76 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Рисунок 2.1 – П и Н волноводы

При тех же габаритных размерах они имеют большую критическую волну основного типа Н10 чем прямоугольные волноводы, в то время как критическая длина волны высшего типа Н20 изменяется мало. Рабочий диапазон частот П- и Н- волноводов, по этой причине, значительно шире чем у прямоугольных, а габариты меньше [3,7]. Если соотношение размеров П- и Н- волноводов соответствует рисунку 1.1, то критические частоты у них одинаковы, волновое сопротивление и коэффициент затухания у Н-волноводов вдвое меньше чем у П- волновода [6]. Коэффициент затухания П- и Н- волноводов больше чем у прямоугольных волноводов. П- и Н- волноводы имеют более плавную зависимость волнового сопротивления от частоты по сравнению с прямоугольными волноводами, что облегчает задачу широкополосного согласования. Меняя высоту гребней можно получить достаточно низкое волновое сопротивление равное волновому сопротивлению коаксиальных линий (50 или 75 Ом). Расчёты волнового сопротивления, коэффициента затухания и предельной мощности проводятся по громоздким формулам, приведённым в [3]. Нами они не рассматриваются. Целесообразно размеры П- и Н- волноводов выбирать следующим образом [3]:

размер 2l выбирать на 20% меньше самой короткой длины волны рабочего диапазона min это обеспечивает минимальные габариты при усло-

вии, что волновод остается одноволновым
		2l=0,8∙ min ;		(2.34)
минимальные потери и максимальная пропускаемая мощность при
a	l	0,3 0, 4	;	(2.35)

отношение g/h выбирают в зависимости от требуемого отношения между критическими длинами волн типов Н10 ( кр10) и Н20 ( кр20) с помощью таблицы 2.3 [2],

кр10	.	(2.36)

кр 20

Таблица 2.3 – Значения отношения при различных соотношениях размеров П и Н – волноводов.

g/h	0.1	0.15	0.2	0.3	0.35	0.4	0.5
a/l=0.3	6.3	5.25	4.4	3.7	3.5	3.2	2.8
a/l=0.4	5.6	4.8	4.1	3.6	3.4	3	2.6

2.1.4 Расчет параметров полосковых волноводов

Полосковые волноводы нашли применение в печатных и интегральных схемах СВЧ. Наиболее широко используется несимметричная полосковая линия передачи, представляющая проводник ленточного сечения, нанесенный на диэлектрическую, ферритовую или полупроводниковую подложку на некотором расстоянии от металлической плоскости (рисунок 2.2). Другие типы линий передачи (симметричные, компланарные, щелевые) используется редко [4] и здесь не рассматривается.

Рисунок 2.2 – Несимметричная полосковая линия передачи: b- ширина полоски; t - толщина полоски; d- толщина подложки с относительной диэлек-

трической проницаемостью

9 .

Для расчета параметров несимметричной полосковой линии передач наиболее удобно пользоваться формулами, приведенными в [7].

Погонная ёмкость (Ф/м) :

C1	1.06 10	11	1	b				(t/d<<1, b/d>0.6),		(2.37)
		11
				d
				d
		11		b		t			1
C1	1.06 10		1	b	1	t			(b/d<2),	(2.38)

				d			d
				d			d
		11		b			t		1
C1	1.06 10		1	b	1		t		(b/d>2).	(2.39)

				d				d
				d				d

Волновое сопротивление

314

(t/d<<1) ,

(2.40)

314

)

(b/d<2),

(2.41)

		b			t		1	1
							1
Z B 314	1		d	1		d		(b/d>2).	(2.42)
Z B 314	1			1				(b/d>2).	(2.42)

Передаваемая мощность

P 8.44 10 4		E2 d 2 ln rB	, Вт,	(2.43)

	0		ra

где Е0 – амплитуда напряженности в центре линии (В/м), а значения rA и rB берут из таблицы 2.4.

Таблица 2.4 – Значения коэффициентов rA и rB.

b/d		t/d=0.025	t/d=0.06
	rB	rA	rB	rA
1	5.1289	1.0365 10-1	5.8905	1.3372 10-1
2	7.6705	2.0195 10-2	8.7697	2.2142 10-2
3	10.0405	4.1461 10-3	11.4578	4.5479 10-3
4	12.3280	8.5969 10-4	14.0536	9.4308 10-4
5	14.5661	1.7862 10-4	16.5938	1.9595 10-4
6	16.7708	3.7127 10-5	19.0964	4.0729 10-5
7	18.9514	7.7177 10-6	21.5717	8.4565 10-6
8	21.1137	1.6043 10-6	24.0265	1.7600 10-6
9	23.2617	3.3351 10-7	26.4651	3.8586 10-7
10	25.3981	6.9329 10-8	28.8905	7.6056 10-8

Предельная мощность ограничивается максимально допустимой напряженностью электрического поля вблизи проводника, так как поле внутри линии неравномерно

EMAX		2E0	KH	,			(2.44)
EMAX				,			(2.44)

где КН – коэффициент, учитывающий эту неравномерность
					t
KH	2	2t	4		t	,	(2.45)
		2t
		d			d
		d

Предельная мощность Рпр	при учете неравномерности распределения

поля и Е0 равном пробивному напряжению

K 2

Pnp P 4H . (2.46)

Коэффициент ослабления, обусловленный потерями в проводящих пластинах

Нп/м,

(2.47)

120

где RS поверхностное сопротивление металла:

			RS		2					f0	0	.	(2.48)
			RS						2			.	(2.48)
									2
Коэффициент ослабления обусловленный потерями в диэлектрике д
при 1можно посчитать по формуле
		1							(tg		tg	) .	(2.49)
	д	1			a a

		2
		2
При 1 выражение для длины волны в полосковом волноводе имеет
вид
									0		,		(2.50)
									0
				в
				в				эфф эфф
								эфф эфф
где	0 – длина волны генератора.
При μ=1
									0		.		(2.51)
									0
					в
					в					эфф
										эфф
Здесь:	эфф -эффективная диэлектрическая проницаемость, а												эфф - эффек-
	тивная магнитная проницаемость а в полосковом волноводе
Из (1.61) находим эффективную диэлектрическую проницаемость в по-
лосковом волноводе эфф при μ=1:
											2		(2.52)
									0		.		(2.52)
									0
					эфф
										в
Постоянная времени отрезка полоскового волновода длиной l нахо-
дится из выражения
							l			Zв	C1	l ,	(2.53)

						vф
						vф

а фазовая скорость находится из выражений

vф (2.54)

L1 C1

vф	c	,	(2.55)

эф

где с = 3∙108 м/с – скорость света.

Сопоставляя (1.63) и (1.65) вычислим величину волнового сопротивления полоскового волновода

Zв		1	эфф	.	(2.56)

	vф	C1	с С1

Величина волнового сопротивления находится также из выражения

	23

Z			L1		.		(2.57)
Z	в				.		(2.57)
	в		C1
			C1
Величина амплитуды Im электрического тока на проводящей полоске
находится из выражения:
	I			Um		,	((2.58)
	I	m				,	((2.58)
		m		Zв
				Zв

где Um - амплитуда гармонического напряжения.

Величина амплитуды вектора плотности поверхностного электрическо-

го тока на полоске J mпов находится из выражения:
										J				Im		.												(2.59)
										J		mпов			b	.												(2.59)
												mпов

Волновое сопротивление несимметричной полосковой линии передачи
иногда рассчитывают по уточненным по сравнению с формулами (1.50) -
(1.52) формулам (1.70):
								120														b
								120							эф					,		b		1

Zв			b d			1.393				0.667				ln		b d		1.444				d						(2.60)
Zв		60							d				b										b					(2.60)
		60				ln		8	d				b	,									b	1.
									b				4 d										d
				эф


В формулах				(1.70)				эффективная								диэлектрическая								проницаемости					эф
																													эф
определяется из выражения
										1				1		1		1		p ,								(2.61)
								эф
										2						2


где
						d		12																		b
	1			12		d		,																		b	1
p	1			12		b		,																		d	1
						b																				d	.	(2.62)
								1										2									.	(2.62)
								1
							d	2									b								b
								2
	1			12						0.04				1				,									1
	1			12			b			0.04				1			d	,							d		1
							b										d								d
При b d >1 значение эффективной диэлектрической проницаемости																												эф
																												эф
можно также определять по формуле
					1						1								d	12
					1			1			1			1		1		12	d		.							(2.63)
	эф			2				1		2				1		1		12	b		.							(2.63)
	эф

2.2 Примеры решения типовых задач по расчету волноводов 2.2.1 Примеры решения задач по расчету параметров прямоугольных

волноводов

2.2.1.1 В прямоугольном волноводе сечением 4 3 см2 распространя-

ется волна типа H11 . Волновод заполнен диэлектриком с

1,15 . Частота ко-

лебаний 8 ГГц. Определить фазовую и групповую скорости и длину волны в волноводе.

Решение.

Для того, чтобы найти длину волны и фазовую скорость в прямоугольном волноводе, необходимо определить значения критической длины волны ( кр ) для волны Нmn типа H11

			2				=				2			2	4,8 см

кр
кр	m	2		n		2			1 2		1 2		1 2	1 2
	m	2		n		2			1 2		1 2		1 2	1 2

	a			b						a		b	4	3
и длины волны генератора
					с			3 108			0,0375м		3,75см.
			0		f			8 109			0,0375м		3,75см.
			0

Вычисляем длину волны в прямоугольном волноводе, заполненном ди-
электриком с 1.15.
				0									3,75		5,102см.
				0

в									2				3,75/ 4,8 2
в
						0 /		кр			1,15 1

Затем определим фазовую скорость волны в этом волноводе

3 108

4,082 108 м / с.

1,15 1

3,75

4,8

кр

Вычислим групповую скорость волны. Получим

v c2 /

(3 108 )2

1,917 108

м / с.

4,082 108

гр

1,15 1

Ответ:

4,082 108 м/ с, vгр

1,917 108 м/ с,

5,102см.

2.2.1.2 Прямоугольный волновод сечением 23 10 мм2 служит для пе-

редачи СВЧ импульсов t

6 нс , несущая частота

10 ГГц . Длина линии

50 м . Оценить качественно величину искажения импульсов, вызванных дис-

персией волновода [7].

Указание. Частотная зависимость модуля спектральной плотности прямоугольного СВЧ импульса представлена на рисунке 2.3.

Решение.

Определим значение критической длины волны ( кр ) и критической частоты ( f кр ) для волны основного типа H 10 :

	кр	2 a =2∙2,3 = 4,6 см;
	кр
f		c		3 108	6,52 109	6,52ГГц.
f	кр		0,046		6,52 109	6,52ГГц.
		кр	0,046
		кр

Рисунок 2.3 – Частотная зависимость модуля спектральной плотности прямоугольного СВЧ импульса

В диапазоне частот от f1 до f2 (рисунок 2.3) передается большая часть мощности СВЧ импульсов. Вычислим значения частот f1 и f2,:

f1= f0 -		1	1010		1		9,83 109				9,83ГГц ;
f1= f0 -			1010				9,83 109				9,83ГГц ;
			6 10 9
f2= f0 +	1		1010		1		10,167 109				10,167ГГц .
f2= f0 +			1010				10,167 109				10,167ГГц .
			6 10 9
Групповое время запаздывания Δt					волн в				волноводе на пути l можно
оценить по формуле
					l				l
			Δt(l)=							.
			Δt(l)=	vгр	f1			vгр	f2	.
При подстановке в эту формулу выражений (1.19) для определения
групповой скорости волны на частотах					f1	и f2

гр f1 c 1

гр f2 c 1

кр

fкр

получим

кр

Δt(l)=	i		1			1				=	50			1				1
	с										3 10	8
					2				2							2				2

				fкр			f								6,52				6,52
		1		fкр	1		f	кр					1		6,52		1		6,52
														9,83				10,167
				f1			f2
				f1			f2
					5,8 10 9 с			5,8нс.
			Ответ: Δt(l=50м)						5,8 10 9 с				5,8нс.

2.2.1.3 Вычислить размеры поперечного сечения квадратного волновода с воздушным заполнением, если известно, что фазовая скорость волны ти-

па E11 равна 6 108 м / с . Частота передаваемых колебаний 5 ГГц.

Решение.

Запишем выражение для критической длины волны кр :

		2		.


кр
кр		2	n 2
	m	2	n 2

a b

Подставив в это выражение исходные данные задачи ( m=1, n=1, a=b)

получим кр а 2.

Запишем выражение для фазовой скорости для исходных данных зада-

чи

		c			c		.
ф

		2				2

				1
	1	0		1	0
					0

					а 2
			кр

Из последнего выражения находим формулу для расчёта численного значения а и вычисляем это значение:

		2							2			2
	с								2		с
	с		1				0			;	с	2 a	2	2 a		2	2	,
							0						2			2	2
	vф										vф						0
					2		а										0
					2		а
где				c		3 108				0,06м		6см;
где		0		f	5 109					0,06м		6см;
		0		f	5 109

	a						1				0,06			1				0,049 м 49 мм.
			0
								с		2					3 108		2
										2							2
					2 1							2 1
														6 108
								vф
								vф

Ответ: 49 49 мм .

2.2.1.4 Фазовая скорость волны типа H10 в прямоугольном волноводе

равна 5с, где с - скорость света. Определить размеры волновода, если длина волны в свободном пространстве равна 10 см.

Решение.

Запишем выражение для критической длины волны типа H10 в прямоугольном волноводе для исходных данных задачи ( m=1, n=0):

		2						2			=2а.


кр		2		2			2			2
кр
	m		n		1			0

	a		b			a			b

Запишем выражение для фазовой скорости для исходных данных зада-

чи

		c			c			.
ф

		2					2

				1
	1	0		1	0
						2 а
			кр

Из последнего выражения находим формулу для расчёта численного значения а и вычисляем это значение:

		2			2			2
	с				2		с
	с	1	0		,		с	4 a		2		4 a		2	2
			0							2				2	2
	vф		2 а				vф								0
															0


a			1			0,1		1					0,051м 5,1см.
		0
					2				с		2
					2						2
		4 1		с			4 1
				с
									5 с
				vф

Ответ: а = 5.1 см; размер b из условий задачи определить нельзя.

2.2.1.5 В волноводе заполненном диэлектриком с относительной проницаемостью 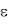2.25 , распространяется волна с фазовой скоростью 3 10 8 м / с . Определить групповую скорость.

Решение.

На любой рабочей частоте имеет место соотношение

			ф гр	c2	/	.
			ф гр
Откуда получим
v	c2 / v	=	(3 108 )2		1,333 108 м / с.
v	c2 / v	=	3 108 2, 25 1		1,333 108 м / с.
гр	ф		3 108 2, 25 1
Ответ: 1,333 108		м / с .

2.2.1.6Определить характеристическое сопротивление волны типа H10

впрямоугольном волноводе сечением 72 34 мм при частоте колебаний 3

ГГц.

Решение.

Вычислим значение величины критической длины волны типа H10 в прямоугольном волноводе для исходных данных задачи ( m=1, n=0):

				2							2		=2а=2∙72=144мм=14,4 см.
кр

				2		n 2		1 2			0 2

			m
			a			b				a		b
Вычислим значение величины длины волны генератора
									с		3 108		0,1м 10см.
							0		f		3 109		0,1м 10см.
							0		f		3 109
Вычислим характеристическое сопротивление волны типа H10
ZCH			Z0				376,7					523,6Ом.

					2			10			2
					2						2
	1			0	1
	1				1
								14, 4
				кр				14, 4
				кр
Ответ:	ZCH			523,6Ом.
2.2.1.7		Определить затухание волны типа H10 в отрезке прямоуголь-
ного волновода сечением 23							10 мм , длиной 10 см на частоте 6 ГГц.

Решение.

Вычислим значения величин длины волны генератора

с 3 108

0 f 6 109 0,05м 5см

и коэффициента

2	0	6,28 5 1,256см 1.
	0

Вычислим поперечное волновое число для исходных данных задачи ( m=1, n=0)

		m	2	n	2	1		2	0	2		3,14
g		m		n		1			0			3,14	1,365см 1

		a			b		a		b		а	2,3
		a			b		a		b		а	2,3
	и продольное волновое число

h		2 g 2 = h				1, 2562		1,3652				j0,534см 1.
h		2 g 2 = h			jh	1, 2562		1,3652		0, 285		j0,534см 1.

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023699.49 Кб4Английский язык..pdf
#
05.02.2023894.6 Кб36Антенны и устройства СВЧ. Микроволновые антенны и устройства СВЧ-1.pdf
#
05.02.20232.4 Mб100Антенны и устройства СВЧ. Микроволновые антенны и устройства СВЧ.pdf
#
05.02.20232.47 Mб204Антенны и устройства СВЧ. Часть 1. Устройства СВЧ.pdf
#
05.02.20231.19 Mб85Антенны и устройства СВЧ.-1.pdf
#
05.02.20232.76 Mб42Антенны и устройства СВЧ.-2.pdf
#
05.02.2023295.32 Кб39Антенны и устройства СВЧ.-3.pdf
#
05.02.202311.7 Mб40Антенны и устройства СВЧ..pdf
#
05.02.20234.31 Mб61Антенны и фидеры.-1.pdf
#
05.02.20234.19 Mб43Антенны и фидеры..pdf
#
05.02.20232.43 Mб27Антенны.-1.pdf