
Теория автоматического управления.-5
.pdf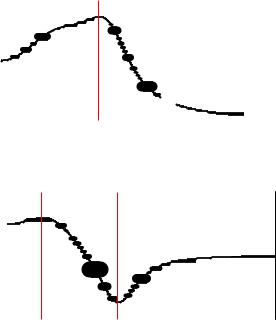
51
0 0.1 100
Амплитудная частотная характеристика
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
36.737 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рад/с |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
20 |
|
|
40 |
60 |
|
|
|
|
80 |
|
|
100 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
|
|
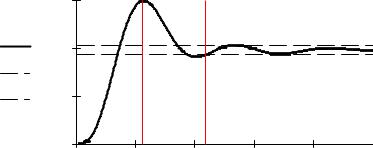
Вещественная частотная характеристика |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
13.638 |
|
|
41.489 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 |
|
20 |
|
40 |
60 |
|
|
|
80 |
|
100 рад/с |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Определение угловой частоты и периода собственных колебаний |
|||||||||||||||||||||||||||||||||||||
переходных характеристик замкнутой САУ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Частота |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
40 Given |
|
|
A |
|
0 k Find |
k 36.737 |
рад/с |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Период |
Tk |
2 |
|
|
Tk 0.171 |
с |
|
|
|
|
|||||||||||||||||||||||||||
k |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Amax A k |
|
|
|
|
|
|
|
|
- максимум АЧХ |
|
|
|
|
||||||||||||||||||||||||
|
|
|
Amax 3.433 |
|
|
|
|
||||||||||||||||||||||||||||||
Показатель колебательности переходной характеристики САУ |
|
||||||||||||||||||||||||||||||||||||
по задающему воздействию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
M |
Amax |
M 1.748 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
A(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
52
Определение частот, соответствующих максимуму и минимуму ВЧХ
18 |
Given |
d |
P |
|
0 |
|
max Find |
|
||
|
|
d |
|
|
|
|
max 13.639 |
рад/с |
||
|
|
|
|
|
|
|
|
|
||
40 |
Given |
d |
P |
|
0 |
|
min Find |
|
||
|
|
d |
|
|
|
|
min 41.489 |
рад/с |
||
|
|
|
|
|
|
|
|
|
||
Pmax P max |
|
Pmin P min - максимум и минимум |
||||||||
|
|
|
|
|
|
|
|
ВЧХ |
|
|
Максимальное перерегулирование, возможное в системе |
|
|||||||||
|
1.18 Pmax 0.277 |
|
Pmin |
|
P(0) |
|
||||
|
|
|
|
|||||||
max |
|
|
|
|
|
|
|
|
100 |
|
|
|
P(0) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
max 83.292 %
6.3.3. Расчет и построение переходных характеристик замкнутой САУ. Определение показателей качества регулирования
Вектор коэффициентов характеристического полинома замкнутой САУ
|
|
|
1 Kp |
|
|
|
|
|
T1 T2 2 T3 1 Kp |
|
|
|
|
|
|
|
|
|
|
|
2 |
||
a |
|
T1 T2 |
2 T1 T3 2 T2 T3 T3 |
|
|
|
|
|
|||
|
2 T1 T2 T3 T1 T32 T2 T32 |
|
|||
|
|
|
|
||
|
|
|
T1 T2 T32 |
|
|
|
|
|
|
|
|
Характеристический полином замкнутой САУ
A(p) a4 p4 a3 p3 a2 p2 a1 p a0

53
Числители передаточных функций замкнутой САУ по задающему и возмущающему воздействиям, производная от характеристического полинома
B(p) |
Kp |
1 p 1 |
C(p) k3 (T1 p 1) (T2 p 1) |
|
|||
|
koc |
|
|
Q(p) d A(p) dp
Корни характеристического уравнения замкнутой САУ
14.162 17.178i
p polyroots(a) |
p |
14.162 17.178i |
||||||
|
8.963 |
40.897i |
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
B(0) |
|
|
|
8.963 |
40.897i |
|
|
y0g gm |
y0g 39.281 |
- установившееся значение |
||||||
A(0) |
||||||||
|
|
|
|
выходной величины при |
||||
подаче задающего воздействия
C(0)
y0f y0g fm y0f 33.885 - установившееся значе- A(0) ние выходной величины при подаче возмущаю-
щего воздействия
Переходная функция САУ по задающему воздействию
|
3 |
B pk exp pk t |
|
|
|
|
|
yg(t) y0g gm Re |
|
|
|
pk Q pk |
|||
k 0 |
|
|
|
t0 0.1 с - момент подачи возмущающего воздействия
Переходная функция САУ по возмущающему воздействию
|
3 |
C p exp |
p |
k |
(t t0) |
|
|
|
|
k |
|
|
|
|
|
yf(t) y0f fm Re |
pk Q pk |
|
|
||||
k 0 |
|
|
|
|
|
|
|
yf(t) if(t t0 y0g yf(t))
|
|
54 |
|
|
|
t 0 0.001 0.5 |
|
|
|
|
|
60 |
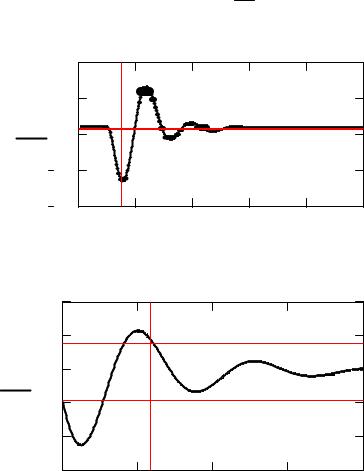
ПХ САУ по задающему воздействию |
|
|||
|
|
|
|
|
|
yg(t) |
0.112 |
0.218 |
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
1.05y0g |
|
|
|
|
|
0.95y0g |
|
|
|
|
|
20 |
|
|
|
|
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
с |
|
|
|
t |
|
|
|
|
|
|
|
|
Показатели качества регулирования по задающему воздействию
Время, соответствующее первому и второму максимумам переходной характеристики (с)
t 0.12 |
Given |
d |
yg(t) |
|
0 |
tm1 Find(t) |
tm1 |
0.112 |
|
|
dt |
|
|
|
|
|
|
t 0.27 |
Given |
d |
yg(t) |
|
0 |
tm2 Find(t) |
tm2 |
0.266 |
|
|
dt |
|
|
|
|
|
|
Значения первого и второго максимумов переходной характеристики
ygm1 yg(tm1) |
ygm1 |
59.754 |
ygm2 yg(tm2) |
ygm2 |
41.237 |
Значения перерегулирования (в %) и колебательности переходной характеристики по задающему воздействию
z |
ygm1 y0g |
100 |
z 52.12 |
|
ygm1 |
1.449 |
||
y0g |
ygm2 |
|||||||
|
|
|
|
|
|
|||
Время переходного процесса по задающему воздействию (с) |
||||||||
t 0.25 Given |
yg(t) |
|
0.95 y0g |
tpz Find(t) |
tpz 0.218 |
|||
|
||||||||
|
||||||||
|
|
|
55 |
|
|
|
|
Период и частота собственных колебаний переходных характерис- |
|||||||
тик САУ (с и рад/с) |
|
|
2 |
|
|
||
Tk tm2 tm1 |
Tk 0.154 |
k |
k 40.901 |
||||
Tk |
|||||||
t 0 0.001 1 |
|
|
|
|
|||
|
|
|
|
|
|||
|
400 |
ПХ по возмущающему воздействию |
|
||||
|
|
|
|
|
|
||
|
200 |
0.153 |
|
|
01.059 y0f |
||
|
|
|
|
||||
yf(t) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
200 |
|
|
|
|
|
|
|
400 0 |
0.2 |
0.4 |
0.6 |
0.8 |
|
|
|
|
|
t |
|
|
|
|
t 0.6 0.601 1 |
|
|
|
|
|
||
|
Участок ПХ по возмущающему воздействию |
|
|||||
|
38 |
|
|
|
1.05y0f |
||
|
|
0.718 |
|
|
|||
|
36 |
|
|
|
|
||
|
|
|
|
|
|
||
yf(t) |
34 |
|
|
|
0.95y0 |
f |
|
|
32 |
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
280.6 |
0.7 |
0.8 |
|
0.9 |
1 |
|
|
|
|
t |
|
|
|
|
56
Показатели качества регулирования по возмущающему воздействию
Время окончания переходного процесса по возмущающему воздействию (с)
t 0.72 Given |
yf(t) |
|
1.05 y0f |
tpv Find(t) |
|
||||
|
||||
tpv tpv t0 |
tpv 0.62 |
|
||
Время, соответствующее минимуму переходной характеристики
САУ по возмущающему воздействию (с) |
|
||||||||
t 0.15 Given |
|
d |
yf(t) |
|
0 |
tmin Find(t) |
tmin 0.153 |
||
|
|
|
|
dt |
|
|
|||
Минимум и перерегулирование переходной характеристики |
|||||||||
САУ по возмущающему воздействию (%) |
|
||||||||
yfm yf(tmin) |
|
|
yfm 261.607 |
|
|||||
v |
y0f yfm |
100 |
v 872.038 |
|
|||||
|
|
|
|||||||
y0f
6.4.ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 3. ПОСЛЕДОВАТЕЛЬНАЯ КОРРЕКЦИЯ ДИНАМИЧЕСКИХ СВОЙСТВ САУ
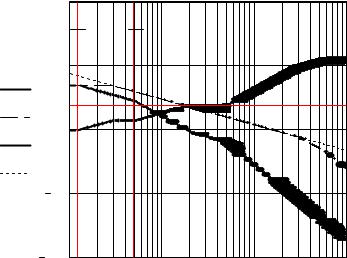
6.4.1. Построение желаемой ЛАЧХ САУ, ЛАЧХ
корректирующего устройства
2.5 |
Lg 20 |
- параметры, взятые из табл. 4.2 |
|||||||
|
|
|
|
|
для |
|
20% |
||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
tnn 0.05 |
cp |
|
cp 157.08 - частота среза |
||||||
|
|
|
|
||||||
|
tnn |
||||||||
|
|
|
|
|
|
для желаемой ЛАЧХ |
|||
Gx1 |
cp |
- прямая, проходящая через частоту |
|||||||
20 log |
|
|
|
|
среза с наклоном -20 дБ/дек |
||||
|
|
|
|||||||
|
|
|
|
||||||
|
|
|
|
57 |
|
|
1 1.1 1000 |
|
|
|
|
||
|
100 |
|
Построение ЛАЧХ коррект. устройства |
|
||
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
T1 |
T2 |
|
|
|
Ga |
50 |
|
|
|
Lg |
|
|
|
|
|
|
|
|
Gg |
|
|
|
|
|
|
Gk 0 |
|
|
|
|
|
|
Gx1 |
|
|
|
|
|
|
дБ 50 |
|
|
|
|
|
|
|
100 |
1 |
10 |
100 |
|
3 |
|
|
1 10 |
||||
|
|
|
|
|
|
|
6.4.2.Синтез передаточной функции корректирующего устройства. Определение передаточных функций скорректированной системы
ЛАЧХ корректирующего устройства имеет следующие на-
клоны: |
|
1 |
|
|
|
|
- |
0 при 1 |
, это соответствует единичному коэф- |
||||
|
||||||
|
|
T1 |
||||
|
фициенту передачи корректирующего устройства; |
|||||
- |
+20 дБ/дек при |
1 |
3 , это соответствует форси- |
|||
|
||||||
|
|
|
|
T1 |
||
|
рующему звену с постоянной времени k1 T1; |
|||||

|
|
|
|
|
|
|
|
|
|
58 |
|
|
|
|
|
|
- |
0 при |
3 |
1 |
|
, |
это соответствует |
инерционному |
|||||||||
|
|
|
||||||||||||||
|
|
|
|
|
T2 |
|
|
|
|
1 |
|
|
||||
|
звену с постоянной времени T |
|
; |
|
||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
1 |
k1 |
3 |
|
||
- |
+20 дБ/дек при |
|
|
|
, это соответствует форси- |
|||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
T2 |
1 |
|
|
|
|
|||||
|
рующему звену с постоянной времени k2 T2 ; |
|||||||||||||||
- |
0 при |
|
1 |
|
1 |
|
это соответствует |
инерционному |
||||||||
|
|
T3 |
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
||||||
звену с постоянной времени Tk1 1;
-+40 дБ/дек, это соответствует двум последовательно включенным форсирующим звеньям с постоянной времени k3 T3;
- +20 дБ/дек при |
1 |
, это соответствует инерци- |
|
||
|
1 |
|
|
T3 |
|
онному звену с постоянной времени Tk2 1 ;
1
-0 при 1 2 , это соответствует инерционному звену с постоянной времени Tk3 1 .
2
Таким образом, корректирующее устройство представляет собой трехзвенный фильтр с передаточной функцией
|
(T p 1)(T |
p 1)(T p 1)2 |
|
||
Wк(p) |
1 |
2 |
3 |
. |
|
( 1p 1)(Tк1p 1)(Tк2 p 1)(Tк3p 1) |
|||||
|
|
||||
Выведем передаточные функции скорректированной САУ относительно задающего воздействия:
- передаточная функция разомкнутой системы
59
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(T p 1)(T p 1)(T p 1)2 |
|
|
|
|
|||||||||||||||
Wpg,c(p) Wк(p) Wpg(p) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Kp |
|
|
( 1p 1)(Tк1p 1)(Tк2p 1)(Tк3p 1) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
koc |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
(T p 1)(T p 1)(T |
2p2 2 T p 1) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Kp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(T p 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|||
|
|
|
koc |
(T |
2 p |
2 2 T p 1)(T |
p 1)(T |
p 1)(T |
p 1) |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
к1 |
|
|
|
|
к2 |
|
|
|
|
|
к3 |
|
|
|
|
|
||||||||
|
|
|
- передаточная функция разомкнутой цепи |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Wpц,,c(p) Wрg,c(p) Woc(p) Wрg,c(p) koc |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
p |
(T p 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
||||
|
|
|
|
|
(T 2p |
2 2 T p 1)(T |
|
|
p 1)(T |
|
p 1)(T |
|
p 1) |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
к1 |
|
|
|
к2 |
|
|
|
к3 |
|
|
|
|
|
|
|
|
||||||||||
|
|
- передаточная функция замкнутой скорректированной |
||||||||||||||||||||||||||||||||||||||||||||
САУ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wрg,c(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
W |
|
(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
зg,,c |
|
|
|
|
|
|
1 Wрg,c(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Kp |
(T p 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
oc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(T 2p2 2 T p 1)(T |
|
|
|
p 1)(T |
p 1)(T |
|
p 1) |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
к1 |
|
|
|
|
|
|
к2 |
|
|
|
к3 |
|
|
|
|
|
|
|
(*) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
(T p 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
(T 2p2 |
2 T p 1)(T |
|
|
p 1)(T |
|
p 1)(T |
|
p 1) |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
к1 |
|
|
|
|
к2 |
|
|
|
к3 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Kp |
(T p 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
oc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
(T |
2p2 |
2 T p 1)(T |
|
|
p 1)(T |
|
|
p 1)(T |
|
p 1) K |
p |
(T p 1)2 |
||||||||||||||||||||||||||||||||||
3 |
|
|
|
3 |
|
|
к1 |
|
|
|
|
|
|
|
|
|
к2 |
|
|
|
к3 |
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||
В скорректированной САУ произошла компенсация (сокращение) постоянных времени T1, T2 и 1, скорректированная система стала иметь пятый порядок.

60
6.4.3. Расчет переходной характеристики
скорректированной САУ. Настройка системы на заданное перерегулирование
Расчет переходной характеристики скорректированной САУ проводится аналогично расчету переходной характеристики нескорректированной САУ. Ввиду громоздкости выражений коэффициентов характеристического полинома скорректированной системы некоторые из них представлены в виде сумм отдельных составляющих. В общем случае они могут быть получены с помощью команды Polynomial Coefficients символьного процессора.
1 |
|
1 |
|
1 |
|
||||
Tk1 |
|
|
Tk2 |
|
|
Tk3 |
|
|
|
3 |
1 |
2 |
|||||||
|
|
|
|||||||
Bc(p) Kp (T3 p 1)2 koc
- новые постоянные времени инерционных звеньев, входящих в корретирующее устройство
ac0 1 Kp |
ac1 2 2 Kp T3 Tk3 Tk1 Tk2 |
|||
ac12 |
(1 Kp) T32 2 Tk1 2 Tk3 2 Tk2 T3 |
|||
ac22 |
(Tk2 Tk3) Tk1 Tk2 Tk3 |
ac13 (Tk3 Tk1 Tk2) T32 |
||
ac2 |
3 |
2 Tk2 2 Tk3 Tk1 |
2 Tk2 Tk3 T3 |
|
|
|
|
|
|
ac33 |
Tk2 Tk3 Tk1 |
|
||
|
|
|
|
1 Kp |
|
|
|
2 2 Kp T3 Tk3 Tk1 Tk2 |
|
||
|
|
|
|||
|
|
|
ac12 ac22 |
|
|
ac |
|
ac13 ac23 ac33 |
|
||
|
|
||||
|
|
|
|
|
|
|
[(Tk2 |
Tk3) Tk1 Tk2 Tk3] T32 2 Tk2 Tk3 Tk1 T3 |
|||
|
|
T3 |
2 |
Tk1 Tk2 Tk3 |
|
|
|
|
|
||
