Квантовая и оптическая электроника.-2
.pdf
41
Из графика рис. 1.7 видно, что для получения максимального излучения необходимо использовать зеркала с коэффициентом отражения, равным 0,7 (r=r1× r2=0,8).
2 вариант. Оптимальный коэффициент отражения зеркал находим из следующей формулы
|
|
|
|
|
|
|
|
|
|
|
|
|
s × (1 - r2 ) |
|
|
c × L |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
P(r2 ) = |
|
|
|
× |
|
|
|
|
, |
(1.66) |
||
h× (1 + r ) |
|
1 |
|
|
||||||||
|
2 |
|
|
a × 2L + ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
r |
× r |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
где s – эффективное сечение среды, h – параметр насыщения, c( c0a )– ненасыщенный показатель усиления среды, r1 – коэффициент отражения глухого зеркала, r2 – коэффициент отражения выходного зеркала.
Подставив в (1.66) числовые значения параметров, получим график и расчетные значения мощности излучения Ризл.уд =f(r1 r2).
|
1.2 |
|
|
P(R2) = |
|
|
|
0.96 |
|
|
|
|
|
|
|
1 |
|
|
1.012 |
P(R2) |
0.8 |
|
|
1.028 |
|
|
1.017 |
||
|
|
|
|
|
|
0.6 |
|
|
0.981 |
|
0.4 |
|
|
0.914 |
|
0.5 |
1 |
0.795 |
|
|
0 |
|||
|
|
R2 |
|
0.568 |
|
|
Рис. 1.8 |
|
|
Из графика рис. 1.8 видно, что для получения максимального излучения необходимо использовать зеркала с коэффициентом отражения, равным 0,4 (r=r1× r2=0,4).
1.2.25. Резонатор оптического квантового генератора образован зеркалами с коэффициентами отражения r1=r2=0,5, распо-
42
ложенными на длине L друг от друга. Активная среда занимает всё пространство между зеркалами.
Как нужно изменить коэффициент квантового усиления активной среды для выполнения условия самовозбуждения генератора, если в резонатор вносится поглотитель, поглощающий 50% падающего на него излучения (не учитывать дифракционные потери на зеркалах и в материале активной среды и зеркал)?
Решение. Пусть от зеркала 1 к зеркалу 2 начинает распространяться волна с интенсивностью I0 . Если поглотитель расположен на расстоянии L1 от первого зеркала, то до поглотителя дойдет волна интенсивностью I0eχa L1 , где χa – коэффициент квантового усиления активной среды.
Пусть α1 определяет долю поглощаемой поглотителем интенсивности, и тогда после поглотителя интенсивность волны
равна
I0 (1− б1 )eχa L1 .
Далее волна опять усиливается в среде и на зеркало 2 при-
ходит с интенсивностью
I0 (1− б1 )eχa L1 eχa L2 = I0 (1− б1 )eχa L .
После отражения от зеркала 2 в направлении зеркала 1 бу-
дет распространяться волна с интенсивностью rI0 (1 − б1 )eχa L .
На обратном пути к зеркалу 1 она испытывает усиление в активной среде и поглощение в поглотителе, после отражения от зеркала 1 интенсивность волны составит
r2I0 (1− б1 )2 e2χa L .
Условие существования в резонаторе самоподдерживающейся волны получается, если приравнять интенсивность исходной волны и волны, совершившей обход резонатора.
I0 = r 2 I0 (1− б1 )2 e2χa L ,
r |
2 |
2 |
2χa L |
= 1. |
(1.67) |
|
(1 − б1 ) e |
|
Откуда условие для порогового коэффициента усиления имеет вид:
|
|
|
43 |
|
|
|
|
|
χa L = |
1 |
ln |
1 |
= ln |
|
1 |
|
. |
|
r2 (1 − б1 )2 |
r(1 |
− б1 ) |
|||||
2 |
|
|
|
|||||
При отсутствии поглотителя б1 = 0
χ0a L = ln 1. r
Очевидно, что отношение пороговых коэффициентов усиления для среды без поглотителя и с поглотителем будет:
|
1 |
|
|
||||
χa |
= |
ln |
|
|
|
|
. |
r(1− б1 ) |
|||||||
|
|
|
|||||
χa0 |
|
|
ln |
1 |
|
|
|
|
|
r |
|||||
|
|
|
|
||||
При r=0,5 и при б1 =50% , получим χa/ / χ0a = 2 .
Таким образом, пороговый коэффициент усиления среды с поглотителем вдвое выше, чем без поглотителя.
1.2.26. Можно ли добиться генерации для активного кристалла длиной 8 см, который дает полуторократное усиление сигнала при условии, что Æ0=0,1см и δ = 0,02 см (Æ0 – ненасыщенный показатель усиления среды, δ – показатель распределенных потерь в среде).
Решение. В результате однократного отражения излучения на зеркалах в резонаторе остается относительная величина потока, равная r1 × r2 . Поскольку однократному отражению на каждом зеркале соответствует два прохода, то условие возникновения генерации соответствует неравенству
|
|
k2 |
(r × r ) > 1, |
(1.68) |
|||
|
|
0 |
1 |
2 |
|
|
|
где k0 – ненасыщенный коэффициент усиления. |
|
||||||
В нашем случае |
k0 = 1,5, |
значит, условие будет выглядеть |
|||||
так: 2,25(r × r ) > 1 , откуда r × r |
= |
1 |
= 0,44 . |
|
|||
|
|
||||||
1 |
2 |
1 |
2 |
2,25 |
|
||
|
|
|
|
|
|||
44
Далее, используя условие c |
|
- d - |
1 |
× ln(r × r )− |
1 |
>0, получим |
||||||
0 |
2 |
|||||||||||
|
|
|
|
l |
1 |
2 |
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
1 |
× ln(0,44)− |
|
|
|
|
||||
численное его решение 0,1 - 0,02 - |
|
|
> 0 . Если это |
|||||||||
2 |
|
|||||||||||
|
||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
||
условие выполняется, то генерацию с этим кристаллом получить можно. В результате получаем 0,03>0.
Ответ: В кристалле длиной l = 8 см генерацию можно получить.
Монохроматичность. Когерентность. Направленность.
1.2.27. Рассчитать число типов колебаний для активного вещества, если степень монохроматичности равна m = Dn / n0 = 10−3 . Активное вещество помещено в резонатор длиной L = 1 см, поперечный апертурный размер зеркал равен D = 1 см, рабочая частота n0 = 3 ×1014 Гц. Как изменится число типов колебаний, если
длина резонатора L = 100 см, а монохроматичность ν |
= 10−6 . |
|
n0 |
Решение. Число типов колебаний в объеме V в интервале частот ν определяется по формуле (1.61). Объем, занимаемый
веществом, равен V = p × D 2 × L . Подставляя в (1.61) формулу
4
для объема, получим следующее соотношение для числа типов колебаний
DN = |
8 × p× no2 |
× p× D2 × L × n0 |
×10−6 |
|
|
|
|
|
. |
(1.69) |
|
|
4c3 |
|
|||
|
|
|
|
|
|
Подставляя в (1.69) заданные значения параметров и длины резонатора L=1 см, получим
DN = |
2 ×(3,14)2 ×(3×1014 )3 ×(10−2 )2 ×10− 2 ×10−6 |
= 20 ×106 , DN=20×106, |
|
||
(3×108 )3 |
|
|
а при длине резонатора L=100 см , DN=20×108.
Ответ: Число типов колебаний увеличится на два порядка.
45
1.2.28. Резонатор образован зеркалами с поперечным размером D=1,5 см, коэффициентом отражения r=r1×r2=0,88. Рассчитать число типов колебаний, возникающих в резонаторе с плоскими зеркалами, для активного твердотельного вещества. Монохроматичность лазера или ширина спектральной линии излу-
чения равна m= nν =10−3 . Расстояние между зеркалами равно
L=8 см. Лазер работает на частоте n = 2 ×1014 Гц. Как изменится число типов колебаний, если кристалл заменить газообразным веществом, при m=10–6 и длине резонатора со сферическими зеркалами L=150 см.
Решение. Число типов колебаний резонатора, распространяющихся внутри угла q, определяется выражением
N(n) = |
L × D4 |
×16 × p3 × n4 × Dn |
или N(n) = |
L × D4 |
×8 × p3 |
× n4 × Dn |
|
|
|
|
|
|
, (1.70) |
||
|
c5 × q2 |
|
c5 × q2 |
/ 2 |
|||
|
|
|
|
|
|||
где Dn – ширина спектральной линии излучения (частотный интервал, в котором содержится половина излучаемой энергии). Величина Dn для резонатора с плоскими зеркалами определяется из формулы (1.27).
Подставляя в (1.27) скорость света и длину резонатора, получаем
|
3 ×108 |
|
10 |
|
|
|
|
Dn = |
|
= 0,18 ×10 |
Гц. |
|
|
||
2 × 0,08 |
|
|
|||||
Для определения |
N(n) необходимо определить q из форму- |
||||||
лы |
|
|
|
|
|
|
|
|
|
|
|
Dn |
= |
q2 |
(1.71) |
|
|
|
|
n |
. |
||
|
|
|
|
|
2 |
|
|
Если генерируются не основные типы колебаний, для которых добротность резонатора может быть равна 90% от добротности для основного типа колебаний, то тогда угол распространения этой моды определяется из соотношения
q » 0,11(1 − r)D , |
(1.72) |
L |
|
а полоса частот излучения лазера будет равняться
46
|
|
|
|
Dn |
|
|
|
−2 |
|
|
|
2 |
D 2 |
|
|
|||
|
|
|
|
n |
= 0,6 |
×10 |
|
|
(1 |
- r |
|
)× |
|
. |
|
(1.73) |
||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
||
Уточним полосу, подставляя данные в(1.73), получим: |
||||||||||||||||||
Dn |
|
|
−2 |
|
|
2 |
1,5 |
2 |
|
|
|
|
−6 |
|
||||
n |
= 0,6 |
×10 |
|
(1 - 0,88 |
) |
× |
|
|
|
= 3,038 ×10 |
|
. |
||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|||||
Число типов колебаний, возникающих в резонаторе с плоскими зеркалами, для активного твердотельного вещества, согласно формуле (1.70), равно
|
8 ×10−2 |
× (1,5 ×10−2 )4 ×8 ×3,143 × (2 ×1014 )4 × 0,18 ×1010 |
23 |
N(n) = |
|
|
= 3,913 ×10 . |
|
(3 ×108 )5 ×3,038 ×10−6 |
||
|
|
|
По второму условию задачи для резонатора со сферическими зеркалами Dn равно
|
|
|
|
Dn = |
|
c |
. |
(1.74) |
|
|
|
|
|
|
|||
|
|
|
|
4 |
× L |
|
||
|
|
Откуда следует Dn=0,5×108. Число типов колебаний в этом |
||||||
резонаторе будет равно |
|
|
|
|||||
|
/ |
|
150 ×10−2 |
× (1,5 ×10−2 )4 ×8 ×3,143 × (2 ×1014 )4 ×0,5 ×108 |
25 |
|||
N |
|
(n) = |
|
|
|
|
|
= 7,166 ×10 . |
|
|
(3 ×108 )5 ×8,64 ×10−9 |
||||||
|
|
|
|
|
||||
Ответ: Во втором случае число типов колебаний будет в 183 раза больше.
1.2.29. Провести сравнительную оценку длины когерентности для некоторых наиболее применяемых источников света:
1)для белого света t £ 10−4 с;
2)для зеленой линии ртутной лампы ( λ0 = 0,546 мкм) со
|
& |
−13 |
|
спектральной шириной Dl = 100 A ; t = 10 с; |
t = 2 ×10−10 с |
||
|
3) для Не-Nе лазера λ0 = 0,63 мкм; |
f = 1,5 ГГц; |
|
– |
для многомодового режима; |
f = 1,5 ГГц; t = 2 ×10−2 с |
|
|
4) для Не-Nе лазера λ0 = 0,63 мкм; |
||
– |
для одномодового режима. |
|
|
|
Решение. Расстояние, проходимое |
светом за |
время коге- |
рентности, называют длиной когерентности.
47
1.Для белого света, согласно формуле (1.40) Lкогер = c × t = 3 ×108 ×10−4 м.
2.Для зеленой линии, зная ширину спектра генерации, длину когерентности определим по формуле
|
|
|
|
|
Lкогер » c |
Dν |
. |
|
|
|
|
|
(1.75) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляем в (1.40) численные значения параметров, полу- |
|||||||||||||||
чим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lкогер » c × t = 3 ×108 ×10−13 = 3 ×10−5 м. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
c |
3 ×108 |
|
|
|
16 |
|
|
Другой |
|
вариант |
Dn = |
|
= |
|
= |
3 ×10 |
м, |
||||||
|
Dl |
100 ×10−10 |
|||||||||||||
Lкогер = |
c |
16 |
= 1×10 |
−8 |
м, |
|
|
|
& |
= 10 |
−8 |
м. |
|
||
|
|
Lкогер = Dl = 100A |
|
|
|||||||||||
|
3 ×10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Для |
одномодового |
Не-Nе лазера с |
временем |
жизни |
|||||||||||
t = 2 ×1010 длина когерентности будет равна |
|
|
|
|
|
||||||||||
Lкогер = c × 2 ×10−10 = 6 ×10−2 м. |
|
|
|
|
|
|
|
|
|||||||
4. Для Не-Nе многомодовогого |
лазера с временем жизни |
||||||||||||||
t = 2 ×10−2 длина когерентности будет равна |
|
|
|
|
|
||||||||||
Lкогер = c × 2 ×10−2 = 6 ×106 м. |
|
|
|
|
|
|
|
|
|||||||
1.2.30. Определить ширину спектра генерации Не-Nе лазера |
|||||||||||||||
( λ = 0,63 мкм) |
с длиной резонатора |
L = 1 м и количество про- |
|||||||||||||
дольных мод, укладывающихся в пределах спектральной линии,
если длина когерентности в одном случае равна Lкогер |
= 20 см, а |
|||||
|
|
|
|
|
1 |
|
в другом L |
|
= 2 ×102 м. |
|
|||
|
когер2 |
|
|
|
|
|
Решение. Определим интервал между частотами соседних |
||||||
продольных мод |
|
|
|
|
||
Dνq = c |
× L |
= |
3 ×108 |
= 1,5 ×108 с–1 =150 МГц. |
|
|
|
|
|||||
|
2 |
2 ×1 |
|
|
||
Воспользуемся формулой (1.75), дающей зависимость длины когерентности от ширины спектральной линии, и определим ширину спектральной линии для случая Lкогер1 = 20 см,
|
|
|
|
|
48 |
Dν = |
с |
= |
3 |
×108 |
= 1,5 ×109 Гц=1,5 ГГц. |
|
|
×10−2 |
|||
1 |
Lкогер |
20 |
|
||
|
|
||||
|
1 |
|
|
|
|
Вэтом случае, в резонаторе будет генерироваться 10 продольных мод.
Вслучае Lкогер2 = 2 ×102 м,
Dν2 |
= |
с |
|
= |
|
3 ×108 |
= 1,5 ×108 Гц=150 МГц. |
Lкогер |
|
|
×102 ×10−2 |
||||
|
|
2 |
2 |
|
|||
|
|
|
|
|
|
|
|
В этом случае, в резонаторе будет генерироваться 1 продольная мода.
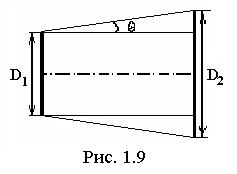
1.2.31. Диаметр светового пучка на выходе газового лазера составляет D = 3 мм. Оценить угол расхождения луча лазера, если на расстоянии 2 м диаметр пятна равен 5,4 мм. Сравнить вычисленный угол расхождения с величиной, определенной теорией дифракции. Длина волны излучения λ = 0,63 мкм. Зеркало круглое.
Решение. Из рис. 1.9 легко можно определить угол расхождения лазерного пучка q.
D1 = 1,5мм × 2, |
D2 = 2,7мм × 2, |
|
|||
R 2 - R1 = 2,7 -1,5 = 1,2 мм = 1,2 ×10−3 , м |
|||||
|
1,2 ×10−3 |
|
= tg(0,6 ×10 |
−3 |
). |
|
|
|
|
||
|
|
||||
q = tg |
2 |
|
|
||
|
|
|
|
|
|
Так как аргумент тангенса весьма мал, то его можно взять за величину q.
Таким образом, q=0,6×10–3 , что соответствует 2/. Теоретически угол расхождения определяется по формуле
qg = |
1,22 × l / D . |
(1.76) |
Это будет равно qg=0,25×10–3 рад или 0,15/. |
|
|
Ответ: qэкспер = 2/ , qтеор |
= 0,15/ . |
|
1.2.32. Определить в вертикальной и горизонтальной плоскости расходимость дифракционно-ограниченного пучка инжекционного полупроводникового лазера, если лазер работает на
|
49 |
длине волны |
λ = 0,85 мкми ширина резонатора t = 10 мкм, |
d = 0,5 мкм , и |
сравнить с расходимостью рубинового лазера |
d = 6,5 мм. |
|
Решение. Угловой коэффициент расходимости полупроводникового лазера в вертикальной и горизонтальной плоскостях определяется по формулам:
|
|
|
|
|
|
|
|
QВ |
= λ , |
QГ |
= λ . |
|
(1.77) |
||||||||
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
t |
|
|
|
|
||
|
|
Подставив числа в (1.77), получим |
|
|
|
|
|||||||||||||||
QВ |
= |
|
0,85 ×10 |
−6 |
|
= 1,7 рад = 97,5 |
O |
; |
|
QГ |
= |
|
0,85 ×10−6 |
= 0,08 рад = 5 |
O |
. |
|||||
0,5 |
×10−6 |
|
|
|
|
10 ×10−6 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Для рубинового лазера: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Q |
|
= |
1,22×l |
= |
1.22×0.69×10−6 |
= 0.13×10−3 рад= 7,5 ×10−3 = 0,45¢ = 27¢¢. |
|||||||||||||||
|
|
|
|||||||||||||||||||
РУБ |
|
|
|
d |
|
|
6.5×10−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
O |
QГ = 5 |
O |
; QРУБ |
′′ |
|
|
|
||||||
|
|
Ответ: QВ = 97,5 ; |
|
= 27 . |
|
|
|
||||||||||||||
1.2.33. Определить оптимальный коэффициент пропускания зеркал Tp (зеркала одинаковые) резонатора, позволяющий полу-
чить максимальную выходную мощность. Коэффициент ненасы-
щенного усиления на проход c0 = 0,1 1 , коэффициент потерь см
a = 0,01 1 , длина резонатора L=10 см. Активная среда заполняет см
весь резонатор. Дифракционными потерями пренебречь. Решение. Стоячую волну в резонаторе лазера можно рас-
сматривать как суперпозицию двух бегущих волн. Пусть каждая из волн характеризуется интенсивностью J. Выходная мощность лазерного резонатора равна
P = TpJ . |
(1.78) |
Удобнее характеризовать потери за счет пропускания зер-
кал.
α = |
Tp |
. |
(1.79) |
|
|||
зер |
λ |
|
|
|
|
|
|
50
В лазере коэффициент усиления из-за насыщения имеет вид:
a = |
|
χ0 |
, |
(1.80) |
|
1 + |
J |
||||
|
J0 |
|
|
||
|
|
|
|
|
|
где J0 – насыщенная интенсивность.
При генерации потери на проход плюс потери на зеркалах должны компенсироваться усилением на проход, т.е. должно выполняться равенство
|
|
|
|
|
|
|
|
|
|
|
|
|
|
χ0 |
|
= aзер + a . |
|
|
|
|
(1.81) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Выразим из (1.81) c0 |
J0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
c |
|
|
|
+ a + |
Ja |
рез |
+ Ja = a |
|
+ a + J |
зер + a , |
||||||||||||||||||||||||||
= 1 + J |
|
|
× (a + a)= a |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
зер |
|
|
рез |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зер |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
J0 |
|
|
|
J0 |
|
|
|
|
|||||||||||||||||
|
|
J0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J0 |
|
|
J0 |
||||||||||
|
|
c0 - aзер |
- a |
|
|
|
|
|
c0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
J = |
|
× J0 |
= J0 × |
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
(1.82) |
||||||||||||||||
|
aзерз |
+ a |
|
|
|
|
|
|
|
|
|
|
1 . |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
aзер + a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Подставляя (1.82) в (1.78), получим |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
P = T |
|
|
× J = a |
|
|
LJ |
0 |
|
|
|
-1 . |
|
(1.83) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
зер |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aзер + a |
|
|
|
|
|
|
|
||||||
Оптимальный коэффициент пропускания зеркал определяется из условия нахождения экстремума выражения (1.79), т.е.
∂ p |
= 0 |
||
∂ α |
зер |
||
|
|||
¶ p |
|
¶ p |
L J0aзерc0 |
|
|
|
|
|
|
|
|
= |
|
|
|
- a |
зер |
L J |
0 |
|
= 0 . |
|
|
|
||||||||
¶ aзер |
|
|
|
aзер + a |
|
|
|
|
||
|
¶ aзер |
|
|
|
|
|
|
|||
Отсюда:
Tp.опт = Laзеропт = L(
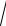c0a - a).
Подставим численные значения
Tp.опт = 10(
0,1×0,01 - 0,01)= 0,22.
Таким образом, оптимальный коэффициент пропускания зеркал резонатора равен Tp.опт = 22% .