Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Квантовая и оптическая электроника.-2

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.74 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 233 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

где J1 и J2 – интенсивность световых полей выделенных интерферирующих пучков; γ эксп – измеряемый в интерферометре контраст интерференционных полос.

В случае генерации одной моды на частоте nо, ширина ла-

зерного излучения может быть оценена по формуле
dnT @	8πhν0	Dnp2 ,	(1.42)

	P
где Р – мощность излучения; v0 – резонансная частота			(v0 =
=Q×∆vP).

Степень монохроматичности можно определить по огибаю-

щей спектра, состоящей из нескольких мод:
μ = δν0 / ν0 = δνoc / ν0 ≈ 10−7 .	(1.43)
Временная когерентность и монохроматичность	связаны

между собой. Чем выше степень временной когерентности, т.е. чем больше время когерентности, тем меньше частотный спектр ∆v, занимаемый излучением, и лучше монохроматичность.

Высокую направленность лазерного излучения, возможность фокусировки излучения в пятно чрезвычайно малых размеров обуславливает пространственная когерентность пучка лазера. Направленность излучения характеризуется телесным углом, в котором распространяется большая часть излучения. Как известно, угловое расстояние первого дифракционного минимума от центра дифракционной картины в случае дифракции плоской

волны на круглом отверстии диаметром D равно:
Da	=	1,22 × l	.	(1.44)

		D

1.2 Примеры решения типовых задач

Темы: Квантовые переходы. Энергетические уровни, ширина спектральной линии. Усиление и генерация в квантовых системах.

1.2.1. Определить неопределенность энергии i-того уровня и ширину естественной линии вещества, имеющего время жизни уровня 7 ×10−6 с.

Решение. Если в данный момент времени атом находится в одном возбужденном состоянии Ek , то такое состояние атома неустойчиво. Через время τ атом перейдет в одно из состояний с меньшей энергией Ei . Это время характеризуется изменением

населенности уровня Ek в 2,7	раз. А вероятность спонтанного
перехода определяется из (1.2),	откуда A21 = 1/ τ .

Но даже в идеальном случае, когда на частицу не действуют внешние силы, ширина энергетических уровней конечна. Энергия изолированного атома в возбужденном состоянии записывается

выражением: DE ³ h . 2

Подставляя численные значения для t и h в формулы для А21 и DЕ, получим

A21	=		1	= 0,142 ×106 ;
			×10−6
	7
DE =		6,62 ×10−34			= 0,945 ×10−28	Дж = 5,9 ×10−10	эВ.

			7 ×10−6

1.2.2. Населенность верхнего и нижнего уровней равна соответственно 1×1010 и 0,5×1010 см–3 . Кратность вырождения верхнего уровня 2, нижний уровень не вырожден. Возможно ли в рассматриваемой системе усиление? Поглощение?

Решение. Отношение числа частиц на уровнях i и j с учетом вырождения:

n								E i	- E j
	i	=	g		i	exp(	-			).
n j									kT
			g	j

Для температурной зависимости можно записать:

T =	Ei − E j				.	(1.45)
	n j
				ni
	k ln		/
		~		~
	g j			gi

				23
			~	~
	Условие		усиления ni g j	> n j gi не выполняется. Так как
1×1010			10
		= 0,5 ×10
2		= 0,5 ×10
2			и, таким образом, Т = ±∞. В системе нет ни

усиления, ни поглощения.

1.2.3. Рассчитать доплеровскую ширину линии для лазера с плоско-параллельным резонатором Фабри– Перо на переходе 1,15 мкм. При следующих значениях активной среды:

k =1,38 ×10

−23 Дж

T = 300

K ,

–

постоянная

Больцмана;

M = 2 ×10−24 г ,

с = 3 ×108

Решение.

Произведем оценку DnД с учетом условий задачи

по следующей формуле:

DnD = 2n0

2kT

0 ln 2

(1.46)

Mc2

Центральная частота, при заданном переходе 1,15 мкм, рав-

на n0 =1,15 ×10−6 м.

ν D = 800 МГц .

Подставляя числовые значения, получим:

1.2.4. Как записать соотношение Г21 / Г12 ,

если учесть, что

hν >> kT , что обычно справедливо для квантовых приборов оптического диапазона.

Решение. Из принципа детального равновесия для n 21 = n12 , получим Г12 × N1 = Г21 × N2 . Заменяя в законе Больцмана (1.19) отношение населенностей на отношение вероятностей, получим

следующее выражение

- E

= exp

Г12

Учитывая, что hv >> kT , разложим в ряд экспоненту. Оставив два первых члена ряда, запишем отношение вероятностей в следующем виде

Г	21	= 1 +	hv	21			= Г		+	hn	21
	21			21	или Г			1			21	.	(1.47)
					или Г			1				.	(1.47)
Г			kT			21	12			kT
12

Таким образом, вероятность безызлучательного перехода сверху вниз больше вероятности снизу вверх.

1.2.5. Изобразить контур спектральной линии, если ширина контура спектральной линии на длине волны излучения в 0,63 мкм равна 150 МГц.

Решение. Так как в задаче заданы резонансная частота и ширина контура, то для изображения контура спектральной линии необходимо использовать формулу (1.8).

Так как время естественной релаксации равно ι = 1/ 2π ν , то

преобразуем (1.8) к виду
	2×Dn		2×Dn
g(n) =		=	(2p)2 ×106 ×[Dn2 +104 ×(×n2 -2×n×n0 +n02 )]	,
	(2pDn)2 +(2p×n-2pn0 )2

где n0= 4,7×10–6 м. Просчитываем несколько значений g(n) вблизи n0.

g(n) :=					2 × 150
g(n) :=							(			2)
2		6		2	4	×	(	n	2	2)
	4 × p	× 10	×	150	+ 10	×		n		- 2 × n × 4.7 + 4.7
с интервалом n := -3, -2.9005.. 10 ,									получим график зависимо-

сти g(n).

Вид требуемой кривой представлен на рис. 1.6.

− 4 .10 3.375×10 10

g(ν )2 .10

1.235×10− 11

10
10
0	0	5	10
5	0	5	10
− 3	ν		9.935
Рис. 1.6

1.2.6. Определить коэффициент Эйнштейна по индуциро-

ванным переходам на

длине волны

λ = 0,56 мкм,

если время

жизни по спонтанным переходам t = 0,5 ×10−7 с.

Решение. Спонтанные переходы линейно связаны между со-

бой следующим выражением (1.5). Так как в задаче задано время

жизни по спонтанным переходам t = 0,5 ×10−7 с, то легко опреде-

лить

А21– вероятность спонтанных переходов по формуле (1.2).

Подставляя все численные значения в (1.5), получим величину,

определяющую индуцированные переходы

c3 ×l3

(0,56)3 ×10−18

B =

= 2×10

/(Дж×с

t×

t×8

−7

−34

8×p× h ×c

×p× h 0,5×10

×8×p×6,63×10

При А21=2×108

с–1

частота

перехода равна

n=5,36×1014 Гц.

1.2.7. Атом излучает фотон

с длиной волны l = 0,55мкм.

Известно, что время излучения

t»18×10–14 с. Оценить, исходя из

соотношений неопределенностей для энергии, неточности в оп-

ределении указанной длины волны.

Решение.

При λ = 0,55

мкм; t = 18 ×10−14

с неопределен-

ность

энергии i

уровня

согласно

уравнению

(1.7)

равна

DE =

6,63 ×10−34

= 0,3683 ×10

−20

Дж.

18 ×10−14

С другой стороны, частоту определяем из соотношения

Эйнштейна

0,3683 ×10−20

n =

= 5,55 ×10

Дж.

6,63

×10

−34

Определим длину волны

l = c / n = 3 ×108 / 5,55 ×1014 = 0,54 ×10−6 м.

При сравнении с заданным значением длины волны видно, что несоответствие равно 0,01 мкм.

1.2.8. Пусть отношение населенностей N2/N1 двух уровней, находящихся в термодинамическом равновесии при температуре T=300 К, равно 1/e. Вычислите частоту излучения n, соответствующую переходу между этими уровнями. В какую область электромагнитного спектра попадает излучение с такой частотой?

Решение. В состоянии термодинамического равновесия N1 = N1e ; N2 = Ne2 . Используя выражение (1.24), определяющее значение температуры из закона Больцмана (1.19), находим частоту

	T × k × ln	Ne
		1		300 ×1,3 ×10−23 × ln e
		Ne				12

n =		2	=		= 6	×10 Гц.
	h			6,62 ×10−34

Для определения области спектра, находим длину волны

l =	c	=	3 ×108	= 50 ×10−6 м – инфракрасный диапазон.
	n
		6 ×1012

1.2.9. Если коэффициент усиления в активной среде ca равен 3·10–1 см–1 , то чему равна мощность сигнала в процессе второго прохождения через активное вещество длиной L = 10 см при мощности на входе в активное вещество Р(0, ν0 ) = 1 мВт?

Решение. Выходную мощность можно определить довольно просто из выражения (1.23). Подставляя исходные данные, получим

Pвых = Р0 × еcа×L = 1× e0,3×20 = 403,43 мВт.

1.2.10. Определить число степеней свободы движения в молекуле аммиака (NH3) и углекислого (CO2)газа.

Решение. Многоатомная молекула – это колебательная система со многими степенями свободы, совершающая малые колебания. Число степеней свободы определяется из выражения

3N–5, (1.4 8)

где N – число атомов в молекуле.

Для CO2: 3·3–5=4 степени свободы

Для HN3: 3·4–5=7 степени свободы.

Таким образом, получаем для CO2 – 4 , а для HN3 –7 степеней свободы.

1.2.11. Если газ состоит из молекул, то следует рассматривать поступательное движение атомов внутри молекулы. Определить рабочий частотный диапазон переходов для колебательных энергетических уровней. (Справка: 1эВ = 1,6 ´10−19 Дж ).

Решение. Расстояние между колебательными уровнями разных молекул находится в пределах 0,1¸0,01эВ.

Определим частоту и длину волны для колебательных энергетических уровней с энергией 0,1эВ

	0,16	−19			8
n =		×10	= 0,024 ×1015	Гц, l =	3 ×10	= 12,5 ×10−6 м.
		−34			15
6,62		×10			0,024 ×10
Определим частоту и длину волны для колебательных энер-
гетических уровней с энергией 0,01эВ
		n = 0,0024 ×1015 Гц,		l = 125 ×10−6 м.

1.2.12. Между колебательными уровнями находятся вращательные уровни. Определить рабочий частотный диапазон переходов для вращательных энергетических уровней. (Справка: 1 эВ = 1,6 ´10−19 Дж).

Решение. Расстояние между вращательными уровнями разных молекул находится в пределах 10–3 ¸10–4 эВ.

Определим частоту и длину волны для вращательных энер-

гетических уровней с энергией 10–3 эВ

1,6 ×10−19 ×10−3

3 ×108

−3

n =

= 0,24 ×10

Гц,

l =

= 125 ×10

м.

6,62

×10

−34

0,24

×10

Определим частоту и длину волны для вращательных энер-

гетических уровней с энергией 10–4 эВ

3 ×108

−2

n =

0,24 ×10

Гц, l =

= 125 ×10

м.

0,24 ×10

Оптические резонаторы. Моды резонатора. Потери

1.2.13. Оценить, насколько частота типа колебаний ТЕМ01 отличается от частоты основного типа колебаний ТЕМ00 для пустого резонатора. Резонатор образован плоским и сферическим

(радиус кривизны R1 = ¥ и R2 = 100 см) зеркалами. Длина резонатора L=50 см.

Решение. Собственные частоты основной моды пустого ре-

зонатора
		1
		1
n = n0	q +		arc cos	g1 × g2	.	(1.49)
n = n0	q +	p	arc cos	g1 × g2	.	(1.49)
		p

Для частот высших типов колебаний существует выраже-

ние
n = n0	q + (m + n)		1	arc cos
			1		g1 ×g2	,	(1.50)
					g1 ×g2	,	(1.50)
			p
где n0 = c/2L; g1,2=1–L/R 1,2;		q, m, n – целые числа; R1 ,R2 –					радиу-

сы кривизны зеркал; L – длина резонатора.

Из (1.50) видно, что все моды с постоянной суммой поперечных индексов m+n частотно вырождены.

Частотные ряды двух типов колебаний разного порядка m+n сдвинуты друг относительно друга на величину

Dn = n0 p1 (D(m + n))arc cos 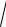g1 ×g2 .

Одно из зеркал резонатора плоское, т.е. его R = ∞ и

g =1 - L =1,

для другого зеркала g = 0,5. Для типа колебаний m=q = 0, n = I имеем:

n01 - n00

3×1010

arc cos

= 74,5 МГц.

arc cos

g1g

0,5

2 ×50 ×3,14

1.2.14.Имеется резонатор объемом V = 1 см3 . Найдите,

сколько мод резонатора находится на полосе λ = 0,01 мкм с центральной длиной волны λq = 0,6 мкм.

Решение. Предполагая, что резонатор образован плоскими зеркалами, определим расстояние в Гц между модами резонатора по формуле (1.26)

		c			3 ×1010	10
Dnq	=			=		= 1,5 ×10	Гц.
		×			2 ×1
	2		L

При длине волны в 0,6 мкм, частота будет

nq =

3 ×108

= 5 ×1014 Гц.

0,6 ×10-6

Число частиц

на уровне определятся выражением

N =

8 × p × n2 × Dn

× V .

(1.51)

N =

8 ×3,14 × 25 ×1028 ×3 ×1016 ×1×10−6

= 0,69 ×1016 .

27 ×1024

В пустом резонаторе уложится

q =

× 2 × L

5 ×1014 × 2 ×1×10−2

= 3,3 ×10

мод.

3 ×108

На заданной

полосе частот Dnл =

= 3 ×1016

уло-

1×10−2 ×10−6

жится

Dnл =

3 ×1016

= 2 ×106 мод.

Dnq

1,5 ×1010

Ответ: 2·106 мод.

1.2.15. Чему равна ширина первого (главного) дифракционного максимума резонатора с плоскими зеркалами диаметром 10 мм, при длине рабочей волны l=0,69 мкм.

Решение. Максимумы интерференции получаются при условии

D ×sina = 2 × k × λ ,	(1.52)
2

где k = 1,2,3,4.

Расстояние от первого дифракционного максимума, заключенного между двумя первыми минимумами, будет определяться из условия

sin q =	λ	,	(1.53)

1	D

где θ1 – угол дифракции, в направлении которого расположен первый минимум. Под таким же углом будет расположен симметричный ему первый минимум. Следовательно, ширина первого (главного) максимума дифракции равна:

Dq1 = 2 × arcsin l , D

если q1 мал, то и sin q1 » q , и для Dq1 можем написать

Dq1 = 2 × l . D

Подставляя численные данные получим,

Dq =	2 × 0,69 ×10−6		= 1,38 ×10−4 рад.

1	10	×10−3

Ответ: Dq1 = 1,38 ×10−4 рад.

1.2.16. Спектральная ширина линии излучения лазера составляет 800 МГц. Центральная частота для излучательного перехода ν0 = 4,74 ×1014 Гц.

1)Определить, какое число продольных типов колебаний может возбуждаться в лазере, если длина резонатора L = 50 см.

2)Оценить, при какой длине резонатора в лазере будет возбуждаться один продольный тип колебаний.

Решение.

Дано:ν0 = 4,74 ×1014 Гц, Dnq = 800 МГц, L = 50 см.

1)Каждому индексу q соответствует своя частота колебаний

νq , определяемая из известного соотношения

νq =

q × c

2 × l

Отсюда легко получаем

q =

2 × L × νq

2 ×50 × 4,74 ×1014

= 158 ×10

×1010

С другой стороны L =

q × lq

. Откуда

q =

2 × L

= c

3 ×1010

= 0,63×10−4 см,

следовательно,

νq

4,74 ×1014

q =

2 ×50

= 158 ×104 .

0,63 ×10

−4

<<< < Предыдущая 1 23 / 233 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023869.01 Кб5Квазисиндромное декодирование II типа алгебраических блоковых кодов..pdf
#
05.02.2023207.11 Кб8Квалиметрия.-1.pdf
#
05.02.2023158.11 Кб5Квалиметрия.-2.pdf
#
05.02.2023158.51 Кб7Квалиметрия..pdf
#
05.02.2023262.55 Кб8Квантовая и оптическая электроника.-1.pdf
#
05.02.20231.74 Mб28Квантовая и оптическая электроника.-2.pdf
#
05.02.2023947.02 Кб19Квантовая и оптическая электроника.-3.pdf
#
05.02.2023485.87 Кб8Квантовая и оптическая электроника.-4.pdf
#
05.02.2023818.12 Кб11Квантовая и оптическая электроника.-5.pdf
#
05.02.20232.68 Mб37Квантовая и оптическая электроника..pdf
#
05.02.2023262.88 Кб8Квантовые и оптоэлектронные приборы и устройства.-1.pdf