Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Квантовая и оптическая электроника.-2

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.74 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2313 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

121

где Pp – плотность мощности накачки.

Определить усиление в среде активного вещества g(Pp ) , ес-

ли

g(P ) = b × (P

- P ) .

(3.87)

Решение. 1. Определяем по (3.86) коэффициент связи

Kсв =

1,14

= 2,3.

10 × 5 ×10−2

0,5

из (3.86) при b = 2 ×10−5 , a = 10−1 ,

2. Определяем P − P

(Kсв +

1) =

(Pp

- P0 ) ×b

, Pp - P0 =

a(K

св +1)2

10−1 × (3,3)2

2 ×10−5

g(P ) =

2 ×10−5

(10−1 ×10,9)

= 1,09 (1/см).

×10−5

Ответ: g(Pp ) = 1,09 (1/см).

3.5.23.

Используя данные в задачах

3.5.21

3.5.22, опре-

делить максимальную мощность излучения (Pmax), которая может быть получена при заданной мощности (PΡ − P0 ), вернее (PΡ ) на-

качки. Примечание: P <<

- P

= 5,4 ×104

Вт

см3

Решение.

Формулу,

определяющую максимальную мощ-

ность излучения (Pmax), запишем в виде

Pизл

= h

1 -

- P )

× (P - P )× V ,

(3.88)

max

P 0

где ηP – коэффициент эффективности накачки, т.е. доля энергии

накачки,

превращенная

в энергию

возбужденных

электронов

( ηP = 0,7 ), V – обьем активного вещества. Он определяется из за-

дач 3.5.21

и 3.5.22 .

V = L × d ×S = 0,05 ×10 ×10−4 × 0,4 ×10−4 = 0,2 ×10−8 см3 .

Подставляя данные в (3.88), получим

изл

−8

Pmax

= 0,7 × 1

×5,4 ×10

×0,2 ×10

= 188 Вт.

×10

−5

Ответ: Pизл

= 188 Вт .

max

122

3.5.24. Определить коэффициент полезного действия (η) лазера по соотношению

h = Pизл P × V ,	(3.89)
p

где Pизл – мощность излучения лазера, определяемая следующим выражением

Pизл = hP × f (a, L)(PP - Pt )V = hP [ 1 − r αL ]. aL 1 + (1 - r)(e -1)

Решение. При оптимальном резонаторе коэффициент полезного действия (КПД) определяется из следующей зависимости:

			P - P					2
			P - P			a		2
h	= h		P 0	1	-			.	(3.90)
h	= h		PP	1	-			.	(3.90)
max		P	PP			b (P - P )
						P	0

Дальнейшее уточнение наибольшего достигаемого КПД лазера следует проводить с учетом его конкретного устройства. В инжекционных лазерах нужно учитывать потери на джоулево тепло, выделяющееся на последовательном сопротивлении RS. КПД можно представить в виде

h =	Hωηg (I − It )	,	(3.91)

	eI2RS + IU
где I – ток накачки, It – пороговый ток, ηg –			дифференциальная

эффективность лазера (отношение приращения мощности излучения к приращению мощности накачки, подведенной к активной области лазера), U – внешнее напряжение, приложенное к p-n- переходу.

Оптимальное превышение порога генерации

				Y	º Iopt	= 1 +		,	(3.92)
				Y	º Iopt	= 1 +	x +1	,	(3.92)
				opt		It
						It
где x =	U		It » Eg	,	ρS –	последовательное			сопротивление,
где x =			It » Eg	,	ρS –	последовательное			сопротивление,
	R	S		lrS jt
		S
приведенное к единице площади p-n-перехода,									jt – пороговая

плотность тока. При токе Iopt достигается наибольший КПД лазера, в случае заданных значений ηg и ξ он равен

h	= h x /(1 +		(3.93)
		x +1)2 .
max	d

123

Совместное нахождение условий для оптимального резонатора и оптимальной накачки приводит к решению, в котором и параметры резонатора, и уровень накачки определяются внутренними характеристиками активной среды. Если Ф0<<α/β*, то решение находится довольно просто и зависит от единой характеристики лазерного материала

ξ∞ = Eξ / lρs j∞ ,

(3.94)

где j∞ – пороговая плотность тока для ненагруженного резонатора, т.е. резонатора, не имеющего внешних потерь излучения.

При этом

η	max	= ξ	∞	(Y −1) / Y			4 .			(3.95)
	max		∞		опт	опт
Зависимости Yопт и ηmax					от ξ ∞ берутся из графиков.
							Например: если ξ ∞ =100,
					то		из	графика		получаем
					Yопт=10, и подставляя в (3.95),
					получим			ηmax,			равное
					h	=105 ×9/104 =			945		= 0,0945.
					h	=105 ×9/104 =					= 0,0945.
					max			104
								104

Ответ: ηmax = 0,0945 .

3.5.25. Определить время затухания в резонаторе для продольных мод (τр), частоту генерации, скорость вынужденного из-

лучения. Если заданы следующие

параметры:

L=0,05 см,

r ×r

= 0,32

; a = 10 см−1

; n=3,6; DE = 2 ×10−2 эВ; E = 1,5эВ.

Решение. Время затухания в резонаторе определим по фор-

муле

(α +

τ p =

) −1 ,

(3.96)

r1 r2

2 L

где Q – добротность резонатора для соответствующего типа колебаний.

Из этого же выражения определим угловую частоту генера-

ции w=Q/tp.

Скорость вынужденного излучения (rst) определим по следующей формуле:

124

		P				2E2
rst	→		=		n		= jηi / cd Eγ ,	(3.97)
				π2h3c3τp
		τp

где Р – плотность мод (число фотонов в единичном энергетическом интервале и единице объема); j – плотность тока накачки; ηi

– внутренний квантовый выход излучения; d – толщина активного слоя; ∆E – ширина спектра генерации; γ – некоторый множитель, зависящий от формы спектра и степени вырождения (т.е. от формы энергетического спектра и температур).

Здесь пороговую плотность (3.73) можно выразить следующим образом:

		2d		E2DEg		1		1
j =	en		×		(a +		ln		) ,

t	p2c2h3			hi		2L r1 × r2

Усиление в активной среде равно [Богд]

g =		p2c2h3h × j
			i t	,
			2d × E2DE × g
	en

так как скорость вынужденного излучения (rst)

rst = c × P(E) × g , n

= n2 × (hn)2 где P(E) .

p2h3c3

(3.98)

(3.99)

равна

(3.100)

(3.101)

9) Определить Pвых инжекционного лазера при увеличении тока накачки на 10 - 50%, если

Pвн = ηWA (I − It ) ,

где It – пороговый ток, I – рабочий ток, ηWA – ватт-амперная диф-

ференциальная эффективность равна
hWA	=	Hw	ln( 1r )			× hp ,
hWA	=	c	a × L + ln( 1	r	)	× hp ,
		c	a × L + ln( 1		)

где ηp – эффективность накачки, т.е. отношение числа электрон- но-дырочных пар, введенных в активную среду лазера, к числу электронов, пересекших p-n-переход.

При определении тока накачки можно также пользоваться скоростью изменения накачки (G)

125

G = hp I 1 , e V

где V – объем активной области.

3.5.26. Электронно-дырочный переход полупроводникового лазерного диода имеет площадь, определяемую размерами 0,245 х х0,048 см2. Пороговый ток через диод составляет 1,1 А. В рабочем режиме, при десятикратном превышении порогового значения по току и напряжению на диоде Uд =1,7 В, излучаемая мощность составляет 1,9 Вт. Определить:

1)плотность тока в пороговом и рабочем режимах;

2)коэффициент полезного действия полупроводникового

ОКГ;

3)величину мощности, рассеиваемой в виде тепла, и плотность потока мощности в хладопроводе, если диод зажат между двумя охлаждающими поверхностями.

Решение.

Задано рабочее значение тока и площадь поперечного сечения

Iраб = 11А, S = 0,01176 cм2 = 1,176 ×10−6 м2 .

Определим плотность порогового тока, она же будет и плотностью рабочего тока

1.1

= 0,94 ×106

, j

= 9,4 ×106

пор

1,176 ×10−6

м2

раб

1,176 ×10−6

м2

Перейдем к определению потребляемой мощности

Pпотр = IрабUд = 11×1,7 = 18,7 Вт, и

если излучаемая

мощ-

ность

равна

1,9

Вт, то мощность

потерь

будет

равна

Pпотерь = 18,7 -1,9 = 16,8 Вт. Следовательно, КПД

легко опреде-

лится, что видно из следующего выражения:

КПД = Pизл 100 = 10,15 % .

Pпотр

Определим коэффициент потерь

kпотерь = 16,8100 = 89,85 % . 18,7

Мощность потерь будем считать равной тепловой мощности

Pпотерь = Pтепловая .

126

Тепловая мощность делится на два потока и определится по

следующей формуле:

P =

Pпот

16,8

= 7,16 ×106 ,

Вт

тепл

2S 2 ×1,176 ×10−6

м2

Ответ:

= 0,94 ×106

; j = 9,4 ×106

;

м2

пор

раб

КПД = 10,15 %; kпотерь = 89,85 %;

= 16,8 Вт; P

= 7,16 ×106

Вт

тепл

м2

Управление пространственными характеристиками

лазерного излучения

3.5.26. Размер пятна в перетяжке гауссова пучка, излучаемого He-Ne лазером видимого диапазона, равен ω0 = 5 мм. Вычислить размер пятна пучка и радиус кривизны поверхности равных фаз на расстоянии 10 м от перетяжки.

Решение. Размер пятна по обе стороны от перетяжки увеличивается по закону, описываемому формулой (3.37). Из формулы

(3.37) следует, что зависимость (ωw ) = f (2z R	) является уни-
0	э
версальной для любого резонатора.

К расчету размеров пятна.

(Здесь z – текущая координата вдоль оси пучка, отсчитываемая от перетяжки, см. рис. 3.13). Эту зависимость можно изобразить в виде графика, показанного на рис. 3.14.

127

Для расчета воспользуемся простой зависимостью (3.36). Длина волны излучения He-Ne лазера λ = 0,63 мкм . Находим из

(3.36) Rэ :

R э = w02 × к = 25 ×10−6			2π		= 249,2 , м.
		0,63 ×10−6

Подставляя параметры в (3.37), получим

w(z) = 5 ×10−3 1+	400			= 5 ×10−3 ×1,0032 = 5,016 ×10−3 , м.

62104
Ответ: w(z) = 5,016 ×10−3 м.

3.5.27.Гауссов пучок с ω0 = 5 мм нужно сфокусировать

таким образом, чтобы перетяжка пучка с размером 50 мкм образовалась на расстоянии 1 м от перетяжки исходного пучка. Какое фокусное расстояние должна иметь линза, и где она должна быть расположена? Лазер He-Ne.

Решение.

Дано: L = 1 м; 2w0 = 10 мм = 10 ×10−3 м; 2w0/ = 100 мкм = 100 ×10−6 м .

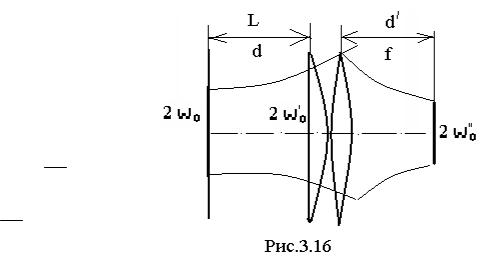
Запишем выражения, определяющие перетяжку пучка внутри резонатора (2w0) и перетяжку, образованную линзой ( 2w0/ ). На рис. 3. 15 показаны размер перетяжки 2w0 для свободного ре-

128

зонатора и размер перетяжки 2w0 за линзой, помещенной в резонатор.

w / =

RЭ/

; w

R э

; к =

2π

(3.102)

Определим конфокальный параметр для падающего пучка

( R э ) по формуле

6,28(5 ×10−3 )2

6,28 × 25 ×10−6

2p(w0 )

R э =

к(w0 )

= 249, м.

0,63 ×10−6

Определим конфокальный параметр сфокусированного лин-

зой пучка ( R э ).

2p(50 ×10−6 )2

6,28 × 2500 ×10−12

Rэ/ = к(w

/ )2 =

= 0,025, м.

0,63

×10−6

0,63 ×10−6

Линза с фокусным расстоянием f

преобразует пучок так,

что выполняются соотношения (3.103).

Rэ

Rэ/

1 -

l - d

1 -

;

. (3.103)

d 2

Rэ 2

Rэ

1 -

Находим из первого уравнения системы (3.103) знаменатель

правой части:

f × Rэ

1 -

Rэ

2 =

1 -

Rэ

;

. (3.104)

Rэ

Rэ/

Подставляем (3.104) во второе уравнение системы (3.103). После некоторых математических операций выразим фокусное расстояние линзы

l - d

1 -

l - d

Rэ

= 1 -

;

Rэ

Rэ/

Rэ

(l - d) -

1 Rэ

Rэ

-1 =

l -

d - d ;

Rэ/

f f Rэ/

129

Rэ

-1

Rэ/

;

Rэ

d - d

Rэ/

f =

104 ×1 -104 d - d

104

(1 - d).

(3.106)

Определяем d, d/

104 -1

104

и f

1 - d

1 -

1 − d − 1 + d

1 − d − d

;

1 -

1 - d

; 2d=1;

d=1/2;

(1 - d)104

1 - d

104

1 - d

f = (1 − d) = 1 − 0,5 = 0,5, м.

Ответ: d=0,5 м, f=0,5 м.

3.5.28. Задан He-Ne лазер c полуконфокальным резонатором длиной 50 см. Для уменьшения расходимости выходного пучка за сферическим (выходным) зеркалом резонатора помещается линза. Какое фокусное расстояние должна иметь эта линза, чтобы размер пятна в образованной за линзой перетяжке пучка составлял 0,95 размера пятна на сферическом зеркале?

Решение. Поставим линзу сразу за вторым зеркалом, т.е. полагаем, что L=d.

В резонаторе на плоском зеркале согласно (3.33)

R1 = ¥, g1 = 1 - 50¥ = 1,

g2 = 1 - 50 = 0 . 50

Размер сечения пучка для основной моды определяется

выражением (3.36). Подставляя в него числовые параметры, получим размер перетяжки на плоском зеркале.

130

				0,5 × 0,63 ×10−6
		Ll			=		= 2,23 ×10−4 =
w =			=			0,5 ×10−2 ×10−6

0	2p			6,28

= 223×10−6 = 223, мкм.

Определим размер пятна на расстоянии 50 см от ω0 по фор-

муле (3.37):

w /				2z 2	= 223×10−6		1	2
	(z) = w	0	1 +			1 +		=

0			Rэ			0,5

= 223×10−6 × 2,23 = 498,6 ×10−6 , м.

Ширина перетяжки, образованной линзой, равна w0// = 0,95 × 498,6 ×10−6 , м = 473 ×10−6 , м.

Пучок ОКГ за линзой имеет такие же закономерности изменения сечения и кривизны волнового фронта, как и пучок без линзы, то есть он может характеризоваться своим местоположением перетяжки и конфокальным параметром. Обозначим расстояние перетяжки от линзы и конфокальный параметр для падающего пучка соответственно через d и R э , а те же параметры для прошедшего через линзу пучка через d′и R′э . Тогда линза с фокусом f преобразует пучок так [Ищенко].

Rэ

2 , (3.107)

Rэ

, 1

Rэ

где согласно (3.36)

Rэ = w0 2 2lπ = 0,49 м, Rэ/ = (w0 // )2 2lπ = 2,23 м.

Перейдем к определению фокусного расстояния линзы. Из

		d	/
	-			находим

второго соотношения (3.107) для 1		f
		f

		d 2	Rэ 2			Rэ		0,49
1	-		+		=		=		= 0,219 .
				2f		Rэ/		2,23
		f

Делая простые арифметические вычисления, из (3.107) находим фокусное расстояние линзы

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2313 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023869.01 Кб5Квазисиндромное декодирование II типа алгебраических блоковых кодов..pdf
#
05.02.2023207.11 Кб8Квалиметрия.-1.pdf
#
05.02.2023158.11 Кб5Квалиметрия.-2.pdf
#
05.02.2023158.51 Кб7Квалиметрия..pdf
#
05.02.2023262.55 Кб8Квантовая и оптическая электроника.-1.pdf
#
05.02.20231.74 Mб28Квантовая и оптическая электроника.-2.pdf
#
05.02.2023947.02 Кб19Квантовая и оптическая электроника.-3.pdf
#
05.02.2023485.87 Кб8Квантовая и оптическая электроника.-4.pdf
#
05.02.2023818.12 Кб11Квантовая и оптическая электроника.-5.pdf
#
05.02.20232.68 Mб37Квантовая и оптическая электроника..pdf
#
05.02.2023262.88 Кб8Квантовые и оптоэлектронные приборы и устройства.-1.pdf