Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Квантовая и оптическая электроника.-2

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.74 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2312 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

111

3.4.11. Сделаем сравнительную оценку выходных параметров 3- и 4-уровневых схем. Если Рвых для рубина при концентрации ионов Cr3+ в рубине 1,6×1019 см–3 , при малых объемах рубиновых элементов, используемых в непрерывном ОКГ (L = 2¸5см, d = 2¸3мм), получается равным примерно около 10Вт. Энергия 1 кванта на длине волны рубинового ОКГ (l=0,69мкм), hw » 10– 19дж; t = 3,4×10–3 сек, tр/tс = 0,5. Достигнутые выходные мощности непрерывных ОКГ на Y3Al5O12:Nd3+ составляют сотни ватт.

Пороговая накачка для 4-уровневой схемы меньше, чем в 3- уровневых. Но нужно отметить следующие обстоятельства:

Величина t для 3-уровневых генераторов (рубин t=3,4×10–3 ) в 10¸30 раз больше, чем t в 4-уровневых ОКГ (стекло с неодимом

t=120×10–6 с, иттрий-алюминиевые гранаты (AYG) имеют t=200×10–6 с).

Полосы поглощения в рубине шире полос поглощения Nd3+ в различных основах, так что эффективность накачки для рубинов является более высокой.

Полупроводниковые лазеры

3.5.12. Лазер на двойной гетероструктуре (ДГС) GaAs/GaAlAs имеет длину резонатора L=300 мкм, коэффициент потерь aa = 10 см−1 и коэффициент отражения граней 0,33. Рассчитать, насколько снизится пороговый коэффициент усиления в результате увеличения коэффициента отражения на одном торце (решать в см).

Решение. Используя соотношение (1.35), определяющее ко-

эффициент усиления вещества:
			1		1
xa	= aa	+		ln			,

			L		r	r

					1	2

где r2и – коэффициент отражения выходного зеркала примем рав-

ным 0,55;

112

– коэффициент

отражения

глухого

зеркала равен

r1 = r / r2 = 0,6 .

Подставляя в него все параметры, получим:

0,56

= 10 +18 = 28 cм−1 .

= 10 +

= 10

−2

−

×10

0,33

Если сделаем r1=1, тогда полное значение коэффициента от-

ражения будет равно

r = 0,55 и

0,3

= 10 +10 = 20 cм−1.

= 10 +

= 10

−2

−

×10

0,55

При увеличении коэффициента отражения

отношение ко-

эффициентов усиления равно

= 1,4 .

xa/

Ответ: Коэффициент усиления уменьшился в 1,4 раза.

3.5.13. Лазер на ДГС, с длиной резонатора L=300мкм, шириной активного слоя S=10 мкм, и толщиной d=0,4 мкм, имеет квантовую эффективность η=0,7, показатель преломления n=4, коэффициент потерь αа=10 см–1 , коэффициент отражения зеркал r=0,33. Рассчитать, как изменится плотность порогового тока при увеличении коэффициента отражения глухого зеркала до 100%.

Решение. По формуле, при

T=0o К,

	=	8π e n2ν2 d ν 1			1			+ α
j					ln				,
		η c2
						r
пор				L					a
							(3.73)
где e –	заряд электрона равен 1,6×10–19
Кл, n –	показатель преломления сре-
ды, ν – резонансная частота,							d –		толщина перехода активной об-
ласти, τ – время жизни перехода 10–10 с, Dn равна 1/t .
Определим			резонансную длину волны для резонатора с

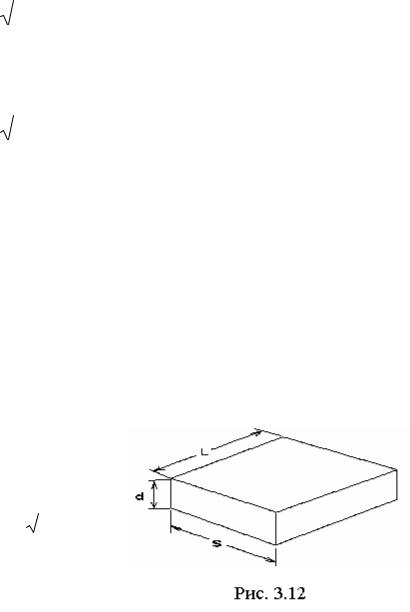
волной типа H110, беря размеры соответственно рис. 3.12.

										113
lp =			2				=			2					» 0,84 мкм = 0,84 ×10−6 м.



	1	2	1	2		1 2		1	2	1	2		1	2
			+		+					+		+

													300
	S		d		L			10		0,4			300

(3.74)

Просчитаем

jпор, подставляя все параметры в (3.73) для раз-

ных коэффициентов отражения зеркал:

a) при r=0,33 и r1=0,6, r2=0,55,

б) при r=0,55 и r1=1, r2=0,55.

8 ×3,14 ×1,6 ×10−19 ×16 ×0,4 ×10

−6

jпор =

×ln

+10

×10

−4

0,7 ×(0,84 ×10−6 ) ×10−10

× ln

103 = 0,33 ×104 × 0,56

+103 = 1,8 ×103 +103 = 2,8 ×103 м-1.

×10−4

0,33

В конечном счете, пороговая плотность получается равной

771,6 ×10−25

2,8 ×10

= 4,4 ×10

×10

−25

×10

= 4,4 ×10

×10−12

×10−10

пор

0,49

м2

б) при r=0,55 и r1=1, r2=0,55

× ln

+103

= 0,33 ×104 × 0,33 +103 = 1,99 ×103 » 2 ×103 м-1,

×10−4

0,55

пороговая плотность равна

771,6 ×10−25

−25

j пор =

× 2 ×10

= 3,15 ×10

×10

= 3,15 ×10

0,49

×10

−12

×10

−10

Ответ: j

= 4,4 ×10

j пор =

3,15 ×10

, т.е. порого-

пор

м2

вая плотность тока уменьшится в ~ 1,4 раза.

3.5.14. По полученным результатам плотности тока в задачах 3.5.12 и 3.6.13 определить мощность излучения лазера для тех же исходных данных.

Решение: определяем пороговый ток по плотности порогового тока

	I0 = j0 ×Sпер ,	(3.75)
где Sпер –	площадь перехода равна (обозначения см. рис. 3.12)
S	= L ×S = 10 ×10−6 × 0,3 ×10−3 = 3 ×10−9	м2 .
пер

114

Тогда пороговый ток равен

= j

×S

= 4,4 ×103 ×3 ×10−9 = 13,2 ×10−6 А.

пер

Вычислим пороговую мощность излучения (мощность неко-

герентного излучения) на длине λо=0,84 мкм

(3.76)

изл

+ 2

Подставляя численные значения параметров, получим

1,87 ×10 3

13 ,2 ×10 − 6

× 0 ,562

3 ×10 8

Pизл =

× 6 ,62 ×10 − 34 ×

0,3 ×10 − 3

1,6 ×10 −19

0 ,84 ×10 − 6

× 0 ,562 + 10

0 ,3 ×10

− 3

262 ×10−32 × 0,65

2 ,87 ×10 3

= 126 ×10−7 = 12,6 ×10−6 Вт.

1,344 ×10−25

Ответ: Pизл=12,6×10–6

Вт = 12,6 мВт.

3.5.15. Используя условия задачи 3.5.12 и 3.6.13,

рассчитать

влияние коэффициента отражения граней на время жизни фотона.

Взять следующие размеры резонатора: длину резонатора L= 300

мкм = 300 10–6 м, D2 –

размер площади торца элемента (D2=S×d),

где S–

поперечный размер резонатора (10×10–6

м),

d –

его высота

(0,4×10–6

м).

Подставляя

значения

получим

D = S × d = (10 × 0,4) ×10−12 .

Взять два варианта коэффициентов от-

ражения: а) r1=0,6,

r2=0,55, r=r1×r2=0,33;

б)

r1=1,

r2=0,55,

r=r1×r2=0,55 при рабочей длине волны λо = 0,84 10–6

м.

Решение. Сделаем анализ времени жизни фотона в резонаторе, используя формулу (1.63а). Добротность Q определяется по формуле (1.62).

Подсчитаем добротность Q для r=0,33, подставив в (1.62) численные значения параметров,

115

2pL

2 ×3,14×300×10−6

6,28×10−4 ×3

18,84×10−4

= 3364.

(1- 0,33+ 4 ×10−12 )

(1- r +

l0L

)

0,84×10−6

10−6 ×53,48

0,5628×10−6

Добротность Q для r=0,55, соответственно, будет равна

2 × 3,14 × 300 ×10−6

6,28 ×10−4

18,84 ×10−4

= 4984 .

0,84 ×10−6 (1 - 0,55 + 4 ×10−12 )

0,84 ×10−6 (0,45)

0,378 ×10−6

Тогда время жизни фотона в первом случае равно

Q × l

3364 × 0,84 ×10−6

−14

−12

= 150 ×10

= 1,5 ×10

ф1

2 × p × C

6,28 × 3 ×10

и во втором

= 2,2 ×10-12 с.

ф2

Ответ: tф

=1,5 ×10−12

c , tф

= 2,2 ×10-12 с.

3.5.16. Используя представленные ниже данные, определить изменения частоты генерации при превышении тока накачки в 2 раза при параметрах лазера, заданных в 3.5.12 и 3.6.13.

Решение. Формулу (3.73), определяющую плотность тока, можно записать так:

−1

6,3 ×104 × n 2 × d × e2 DE

j =

(3.77)

где j – пороговая плотность тока в A/см2; ε – энергия излучения в

эВ (ε = 1,47 эВ); ∆Ε – ширина линии спонтанного излучения в эВ

(∆Ε =0,023 эВ); d – толщина p-n перехода (d = 1,1 10–3 cм); η – квантовый выход (η =0,7); n – показатель преломления (n = 4); χ0 – коэффициент поглощения света (χ0= 10 см–1 ); L – расстояние между двумя отражающими покрытиями (L = 300 мкм); r – коэффициент отражения граней (r = 0,33).

Определим общий коэффициент потерь a=aа+aз, полагая, что c0 = aа,

0,56

см-1.

a = c

=10 +

= 10

+18

= 28

3 ×`102 ×10−4

3 ×10−2

0,33

116

Подставляя числа в (3.77), получим значение плотности тока

j =

6,3 ×104 × 4 ×1,1×10−3 ×1,472 × 0,023 × 28

= 2200

2 .

см

0,7

При ∆Ε = 0,023 эВ определим частоту генерации по форму-

ле (1.7)

0,023 ×1,6 ×10−19

5,5 ×10−3 ×10−19

0,023 эВ

n =

5,5 ×10

Гц,

6,62 ×10

−34

6,62 ×10

−34

Длина волны при этом будет равна

l =

3 ×108

= 0,545 ×10−4 м.

5,5 ×1012

Определим из (3.77) величину ∆Ε, увеличив плотность тока

в 5 раз ( j

= 2 × 2200 = 4,4 ×103 А м2 ).

При этом значении j1 величина ∆Ε равна

DE =

j1 × h

4,4 ×103

= 0,0656 эВ.

6,3 ×104

6,3 ×104 × n 2 × d × e2 × c

×16 ×1,1×10-3 × (2,16) × 28

При новой ширине линии спонтанного излучения, частота

будет равна

0,0656 ×1,6 ×10-19

Гц .

n =

= 1,58 ×10

6,62

×10- 34

А длина волны соответственно

l1 =

3 ×108

= 1,9 ×10

- 5

м.

1,58 ×1013

Ответ: При двукратном превышении тока накачки ширина

спектральной линии уменьшилась в

0,545 ×104

= 2,8 раз.

0,19 ×104

3.5.17.

Определить отношение полного числа фотонов Nф к

числу Nq электромагнитных колебаний различной поляризации в

пределах спектральной линии излучения в кристалле полупро-

водника, две противоположные грани которого образуют объем-

ный

резонатор, при

следующих заданных параметрах лазера:

h = 0,5; I = 105 А/ см2; n02 = 11;

r= 0,35; e= 1,47 эВ; DE= 0,02

эВ.

117

Решение. Упрощенная теория, основанная на предположении однородного распределения фотонов и изотропного распределения их по скоростям, показывает, что это отношение выражается следующей формулой:

	N	=		3 ×p2 × h× h3 × c2 × I
					,	(3.78)

	N0		n02 × (1 - r) × (1 - cos q) × e × e2 × DE
где η – квантовый выход п/п материала ( η= 0,5); ε –						энергия фо-
тонов спектральной линии излучения; E – ширина спектраль-
ной линии; n0 – коэффициент преломления линии; I						– плотность
тока возбуждения, проходящего через p-n-переход; r –						коэффици-

ент отражения от граней кристалла при нормальном падении луча; q – половина угла, в пределах которого распространяются те фотоны, которые претерпевают многократные отражения: (q = =180); e – заряд электрона, скорость света; h – постоянная Планка.

Подставляя заданные численные параметры в (3.78), полу-

чим

(3,14)2 × 0,5 × (4,8 ×10−10 )3 × (3 ×108 )2 ×105

3 ×

× (1 - 0,35) × (1 - cos180) ×16 ×10−19 × (1,47)2 × 0,02

1,73 ×9,85 × 0,5 ×990 ×10−102 ×9 ×1016 ×105

11×

0,65 × (1 - cos180) ×1,6 ×10−19 ×1,472 ×1,63 ×10−57 × 0,02

22260 ×10−81

2,02 ×10−76 × (1 - cos180)

22260 ×10−81

11019 ×10−5

0,11

= 0,055 .

2,02 ×10−76 × (1 - cos180)

1 - cos180

Ответ:

= 0,055 .

118

Определение добротности в полупроводниковых лазерах

3.5.18. Определить нагруженную добротность резонатора полупроводникового лазера тремя вариантами: 1) обусловленную активным поглощением на свободных носителях, 2) определяемую через отражения от торцевых граней кристалла, 3) обусловленную дифракцией.

Численные значения параметров, необходимых при решении следующие:

ε0 – диэлектрическая проницаемость ( ε0 = 10), σ – прово-

димость ( s = 0,5 ×103 Ом–1 см–1 ), τ – время релаксации носителей тока ( t » 0,2 ×10−12 с), длина волны l ( λ = 0,84 мкм), коэффициент

отражения граней r (r=0,3), длина резонатора (L = 5 ×10−2 см), толщина области локализации поля d (d = 10 см).

Решение. Нагруженная добротность для первого варианта может быть определена следующим выражением

Qн = e0 × w2 × t2 .

(3.79)

4 × p × s

Вычислим угловую частоту, при заданной длине волны

w = 2 × p × f =

2 × p × 3 ×10

18,84 ×10

= 22,43 ×1014 рад.

−6

0,84 ×10

Подставляя (3.79) заданные числа, получим величину на-

груженной добротности

10 × (22,43)2 ×1028 × (0,2 ×10−12 )2

10 ×503 ×1028

× (0,2)2

×10−24

160 ×104

Qн

= 320.

4 × p × 0,5 ×103

6,28 ×103

Для второго варианта нагруженная добротность определяет-

ся по формуле (1.62) и равна

2 × p ×e0 ×L

6,28 ×10 × 5 ×10−2

−2

Qн =

= 5,3 ×10

×10

= 5,3 ×10

l × (1 - r)

0,84 ×10−4

× 0,7

Для третьего варианта нагруженная добротность определя-

ется по формуле

QН =

4 × p × d2 × e

(3.80)

где d – толщина области локализации поля.

119

Подставляя в формулу (3.80) численные значения параметров, получим

QН = 4 × p ×10× −6−×10 = 15,0 ×10−1 = 1,5 . 0,84 10 4

Ответ: Для первого варианта QН=320,

для второго варианта – Q Н = 5,3 ×104 , для третьего варианта – QН = 1,5 .

3.5.19. Просчитать плотность энергии собственного поля Uν, на резонансной частоте (λ=0,84 мкм), при T=300 K по формуле Планка для равновесного излучения абсолютно черного тела

8 × p × n2

Uν =

(3.81)

-1

exp

где k

–

постоянная Больцмана ( k = 1,38 ×10−23 Дж × (°K)−1 ),

h –

постоянная Планка ( h = 6,62 ×10−34

Дж × с), частота при задан-

ной длине n = 3,6 ×1014 Гц.

Решение.

Подставляя в (3.81) числа, получим

U =

8×3,14× 46,65×1042 ×6,62×10−34

287,3×10−16

= 526×10−16Дж/ cм3×с.

−34

0,545

8 3

6,26×10

×3,6 ×10

(10 ) ×exp

-1

−23

×300

1,38×10

Ответ: Uν = 526 ×10−16 Дж/ cм3×с.

3.5.20. Оценить мощность порога генерации (Pt) в кристалле GaAs при коэффициенте пропорциональности β , равному:

		1,59 ×10−5			−5	2
b	=			» 2 ×10		см /Вт,	(3.82)
			2 × E2 × DE
		n
где E – ширина полосы ( DE = 2 ×10−2 эВ),							энергия перехода

E = 1,5 эВ, n – показатель преломления ( n = 3,6).

Решение. Мощность порога генерации (Pt) в GaAs при известном коэффициенте пропорциональности b равна:

	120
P = P	+	a	+	ln r1/ 2	,	(3.83)
		b		b × L
t 0

где r = r1 × r2 - коэффициент отражения зеркал 1 и 2 ( r = 0,32 ), L – расстояние между зеркалами (L = 0,05 см), α – коэффициент по-

глощения ( α = 10			см–1 ), P			– порог мощности инверсии ( P = 0,
					0	0
выполняется при низкой температуре).
Подставляем эти данные в (3.83), получаем
P = 0 +		10		+	ln r	= 2 ×106 Вт/см3, если r = r .
	2	×10−5			b × L
t						1 2

Ответ: Pt = 2 ×106 Вт/см3.

3.5.21. При мощности порога генерации в кристалле GaAs Pt ( Pt = 2 ×106 Вт/см3), оценить верхний предел эффективного раз-

мера d p-n-перехода активной области диода, определяемого из формулы

		d =					(3.84)
	d* –	d =		dV / S	,		(3.84)
где	d* –	линейный размер активной области, V –					объем, S –
площадь.
	Решение. При приближенных оценках можно считать
		d =				,	(3.85)
		d =	c × DT / P			,	(3.85)
					t
где	ΔΤ –	допустимый перегрев активной области ( ΔΤ =10 К),
P = 2 ×106		Вт/см3;
t

χ ≈ 10 (Вт/см) – коэффициент теплопроводности. При этих параметрах d = 70 мкм.

Ответ: d = 70 мкм.

3.5.22. Оценить коэффициент связи Kсв резонатора с внешней средой через параметры лазера, если r = 0,32 , α = 10 см–1 , L = 0,05 см.

Примечание: коэффициент связи определяется по формуле

ln×

(Pp

-P0 ) ×b

× r

Kсв

-1,

(3.86)

× L

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2312 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023869.01 Кб5Квазисиндромное декодирование II типа алгебраических блоковых кодов..pdf
#
05.02.2023207.11 Кб8Квалиметрия.-1.pdf
#
05.02.2023158.11 Кб5Квалиметрия.-2.pdf
#
05.02.2023158.51 Кб7Квалиметрия..pdf
#
05.02.2023262.55 Кб8Квантовая и оптическая электроника.-1.pdf
#
05.02.20231.74 Mб28Квантовая и оптическая электроника.-2.pdf
#
05.02.2023947.02 Кб19Квантовая и оптическая электроника.-3.pdf
#
05.02.2023485.87 Кб8Квантовая и оптическая электроника.-4.pdf
#
05.02.2023818.12 Кб11Квантовая и оптическая электроника.-5.pdf
#
05.02.20232.68 Mб37Квантовая и оптическая электроника..pdf
#
05.02.2023262.88 Кб8Квантовые и оптоэлектронные приборы и устройства.-1.pdf