
Физические основы оптоэлектроники.-2
.pdf
б |
kT |
ln |
Nd Na |
, |
|
q |
2 |
||||
|
|
|
|||
|
|
|
ni |
|
где Ge - относительная диэлектрическая проницаемость германия. Подстановка численных значений в выражения (8.13) приводит к следующему результату:
|
1.38 |
10 |
23 |
300 |
|
ln |
2.4 |
1015 |
2.4 |
1015 |
1.38 |
4 |
3 |
10 |
21 |
ln 10 |
|
||||||||||||||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1.6 |
10 |
19 |
|
2.4 |
1013 |
2.4 |
1013 |
|
|
1.6 |
10 |
19 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
10 1 |
|
2.3 |
|
0.2 B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.6 10 19 |
|
|
8.85 10 14 |
2.4 1015 |
|
||||||||||
C S |
|
|
|
q |
Ge 0 |
|
Nd Na |
|
10 |
2 |
16 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
б |
|
V |
|
Nd |
|
Na |
|
|
|
|
|
|
2 |
0.2 |
0.1 |
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
1.6 |
1.6 |
8.85 |
1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
10 |
2 |
|
10 |
17 |
|
10 |
2 |
1.4 10 |
|
16 |
|
1.2 10 |
10 |
Ф. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференциальное сопротивление перехода в области положительных смещений определяется выражением
Rd V0 |
kT |
exp |
qV0 |
, |
(8.14) |
|
qI0 |
kT |
|||||
|
|
|
|
где все величины табличные или легко вычисляются. Поэтому
можно найти величину Rd V0 |
: |
|
|
|
|
|
|
|
|
|||||||||
Rd V0 |
|
|
|
1.38 |
10 |
23 |
300 |
|
exp |
1.6 |
10 |
19 |
0.1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1.6 10 |
19 |
10 |
6 |
10 |
2 |
1.38 |
10 |
23 |
300 |
|
|||||||
|
|
|
|
|
||||||||||||||
4.2 |
10 |
21 |
exp |
1.6 |
10 |
|
20 |
|
2.6 106 exp |
3.8 1.7 105 Ом. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.6 |
10 |
27 |
|
4.2 |
10 |
|
21 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Теперь, используя выражение (8.12), найдем реальную часть импеданса фотодиода на частоте 104 Гц :
81
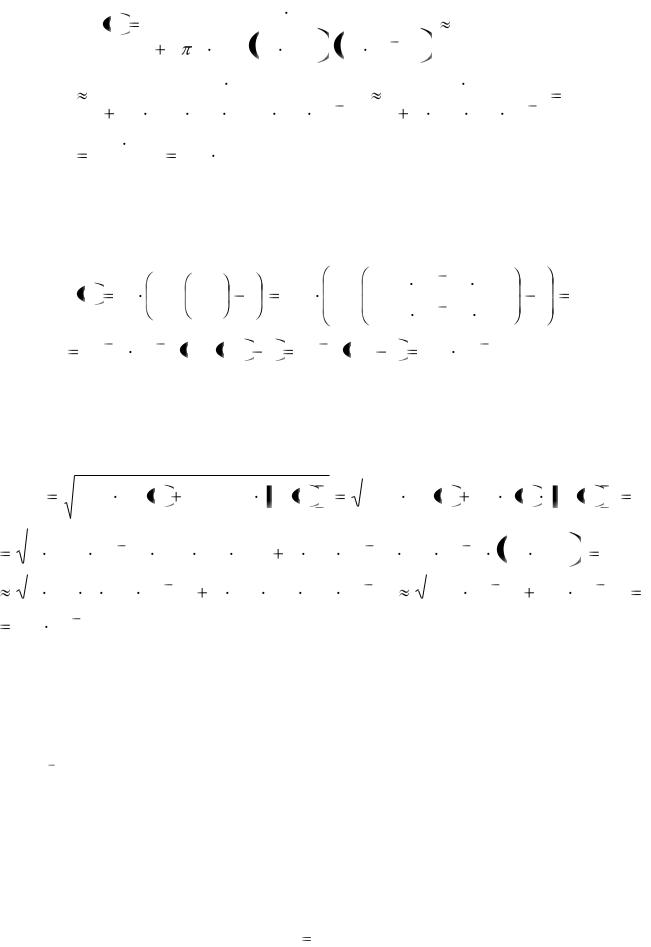
Re Z |
|
|
|
|
|
|
1.7 |
105 |
|
|
|
|
|
|
|
|
|||
|
1 |
4 |
2 |
108 1.7 |
|
105 |
2 1.2 10 10 2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1.7 |
105 |
|
|
|
|
|
|
|
1.7 |
105 |
|
||
1 |
40 |
108 |
2.9 |
1010 |
1.4 |
10 |
20 |
1 |
4 |
2.9 |
1.4 |
10 1 |
|||||||
1.7 |
105 |
|
6.5 |
104 Ом. |
|
|
|
|
|
|
|
|
|
||||||
|
2.6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определим величину постоянного тока, текущего через p-n переход:
I V |
I0 |
exp |
qV |
1 |
i0S |
exp |
1.6 |
10 |
19 |
0.1 |
1 |
|||
|
|
|
|
|
|
|
||||||||
kT |
1.38 |
10 |
23 |
300 |
||||||||||
|
|
|
|
|
|
|
||||||||
10 |
6 |
10 2 exp 1.3 |
1 |
10 |
8 3.7 1 |
2.7 10 8 A . |
||||||||
Теперь можно рассчитать спектральную плотность суммарного шума фотодиода, подставив в выражение (8.11) найденное значение активной части импеданса:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re Z 2 |
|
4kT Re Z 2q I V Re Z 2 |
|
|||||||||||
Uш f |
|
4kT Re Z I |
2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ш дроб |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
1.38 |
10 |
23 |
300 |
6.5 |
104 |
2 1.6 |
10 |
19 |
2.7 |
10 |
8 |
6.5 |
104 2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
1.4 |
3 |
6.5 |
10 |
17 |
2 |
1.6 |
|
2.7 |
4.2 |
10 |
18 |
10.1 10 |
16 |
0.4 |
10 |
16 |
||||||||||
3.2 |
10 |
8 |
|
В / Гц1/ 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, ответ на поставленный в этой задаче вопрос таков: спектральная плотность суммарного шума германиевого фотодиода на частоте 104 Гц при напряжении на нем V 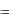 составляет
составляет
3.2 10 8 В / Гц1/ 2.
10 8 В / Гц1/ 2.
8.3.ВАРИАНТЫ ЗАДАНИЙ ПО ОПРЕДЕЛЕНИЮ ПАРАМЕТРОВ ФЛУКТУАЦИОННЫХ ПРОЦЕССОВ
ВПОЛУПРОВОДНИКАХ
ККОНТРОЛЬНОЙ РАБОТЕ № 2
1.Рассчитать амплитуду теплового шума, возникающего на постоянном сопротивлении R 2.6  1010 Ом, находящемся при тем-
1010 Ом, находящемся при тем-
82

|
пературе T |
300 K , если полоса пропускания вольтметра, с по- |
|||||
|
мощью которого производится измерение, составляет |
f |
106 Гц . |
||||
2. |
Рассчитать |
спектральную |
плотность теплового |
шума, |
возни- |
||
|
кающего на постоянном сопротивлении R |
9 108 Ом, находящем- |
|||||
|
ся при температуре T 400 K , если вольтметр, с помощью кото- |
||||||
|
рого производится измерение, настроен на регистрацию пере- |
||||||
|
менного напряжения частотой f 108 Гц . |
|
|
|
|
||
3. |
Рассчитать амплитуду теплового шума, возникающего на по- |
||||||
|
стоянном сопротивлении R |
2 109 Ом, находящемся при темпе- |
|||||
|
ратуре T 500 K , если полоса пропускания вольтметра, с помо- |
||||||
|
щью которого производится измерение, составляет |
f |
108 Гц . |
||||
4. |
Рассчитать величину активного сопротивления, |
находящегося |
|||||
|
при температуре T 300 K , |
если амплитуда регистрируемого на |
|||||
|
нем вольтметром с полосой пропускания |
f 104 |
Гц , |
составляет |
|||
1.7 10 8 В.
10 8 В.
5.Рассчитать величину активного сопротивления, находящегося при температуре T 500 K , если амплитуда регистрируемого на
нем вольтметром с полосой пропускания f 102 Гц , составляет
3.7 10 9 В.
10 9 В.
6.Рассчитать температуру, при которой находится проволочный резистор величиной 109 Ом , если амплитуда регистрируемого на
нем вольтметром с полосой пропускания f 106 Гц , составляет
8.7 10 8 В.
10 8 В.
7.Рассчитать величину активного сопротивления, находящегося при температуре T 300 K , если амплитуда регистрируемого на
нем вольтметром с полосой пропускания f 104 Гц , составляет
4.5  10 9 В.
10 9 В.
8. |
Рассчитать |
напряжение |
суммарного шума в полосе частот |
|
|
f |
107 Гц , |
измеряемого |
на постоянном резисторе величиной |
|
R 2 105 Ом, если к резистору приложено постоянное напряже- |
|||
|
ние величиной V 1.5 В , а температура окружающей среды равна |
|||
|
T |
300 K . |
|
|
9. |
Рассчитать |
напряжение |
суммарного шума в полосе частот |
|
|
f |
106 Гц , |
измеряемого |
на постоянном резисторе величиной |
|
R |
9.1 105 Ом , если к резистору приложено постоянное напряже- |
||
83

ние величиной V 1.5 В , а температура окружающей среды равна
T |
290 K . |
|
10. |
Рассчитать напряжение |
суммарного шума в полосе частот |
|
f 105 Гц , измеряемого |
на постоянном резисторе величиной |
R 5.1 106 Ом , если к резистору приложено постоянное напряжение величиной V 10 В , а температура окружающей среды равна
106 Ом , если к резистору приложено постоянное напряжение величиной V 10 В , а температура окружающей среды равна
T290 K .
11.Рассчитать напряжение суммарного шума на частоте f 10 кГц RC - цепи, составленной из резистора величиной R 5  105 Ом и
105 Ом и
параллельной ему емкости С |
2 106 пФ , если к цепи приложено |
||||
постоянное напряжение величиной V |
2 В , а температура окру- |
||||
жающей среды равна T |
290 K . |
|
|
|
|
12. Рассчитать напряжение суммарного шума на частоте f |
100 кГц |
||||
RC - цепи, составленной из резистора величиной R |
2 104 Ом и |
||||
параллельной ему емкости С |
5 103 пФ , если к цепи приложено |
||||
постоянное напряжение величиной V |
0.1 В , а температура ок- |
||||
ружающей среды равна T 310 K . |
|
|
|
||
13. Рассчитать напряжение суммарного шума на частоте |
f 3 кГц |
||||
RC - цепи, составленной из резистора величиной R |
5.1 104 Ом и |
||||
параллельной ему емкости С |
2.2 106 пФ , если к цепи приложено |
||||
постоянное напряжение величиной V |
10 В , а температура окру- |
||||
жающей среды равна T |
290 K . |
|
|
|
|
14. Рассчитать напряжение суммарного шума на частоте f |
20 кГц |
||||
RC - цепи, составленной из резистора величиной R |
5.1 103 Ом и |
||||
параллельной ему емкости С |
2.2 106 пФ , если к цепи приложено |
||||
постоянное напряжение величиной V |
20 В , а температура окру- |
||||
жающей среды равна T |
350 K . |
|
|
|
|
15. Рассчитать спектральную плотность суммарного шума кремние-
вого |
фотодиода на частоте 104 |
Гц |
при напряжении на нем |
V 0.1 В , имеющего площадь S |
10 2 |
см2 и плотность обратного |
|
0 |
|
|
|
тока |
j0 10 6 А / см2 . Считать уровни легирования p- и n-областей |
||
одинаковыми и равными 2.4 1015 см 3 . |
|
||
16. Рассчитать спектральную плотность суммарного шума германиевого фотодиода на частоте 103Гц при напряжении на нем V0 0.2 В , имеющего площадь S 10 2 см2 и плотность обратного
84

тока j0 10 8 А / см2 . Считать уровни легирования p- и n-областей одинаковыми и равными 2.0  1014 см 3 .
1014 см 3 .
17. Рассчитать спектральную плотность суммарного шума арсе- нид-галлиевого фотодиода на частоте 104 Гц при напряжении на
нем |
V 0.3 В |
, имеющего площадь S 10 2 см2 и плотность обрат- |
|
0 |
|
ного тока j0 |
10 10 А / см2 . Считать уровни легирования p- и n- |
|
областей одинаковыми и равными 1.4  1013 см 3 .
1013 см 3 .
18.Рассчитать спектральную плотность суммарного шума крем-
ниевого |
диода на частоте 3 103 Гц |
при |
напряжении на нем |
V 0.1 В , имеющего площадь S 6 10 2 |
см2 |
и плотность обратного |
|
0 |
|
|
|
тока j0 |
10 8 А / см2 . Считать уровни легирования p- и n-областей |
||
одинаковыми и равными 3.3 1016 см 3 . |
|
|
|
19. Рассчитать спектральную плотность суммарного шума герма- |
|
ниевого диода на частоте 106 Гц при напряжении на нем V 0 В , |
|
|
0 |
имеющего площадь S 7.5 10 2см2 |
и плотность обратного тока |
j0 2 10 7 А / см2 . Считать уровни |
легирования p- и n-областей |
одинаковыми и равными 2.4  1015 см 3 .
1015 см 3 .
20. Рассчитать спектральную плотность суммарного шума арсе- нид-галлиевого диода на частоте 104 Гц при напряжении на нем V0 0 В , имеющего площадь S 10 2 см2 и плотность обратного тока j0 4.5  10 8 А / см2 . Считать уровни легирования p- и n-областей одинаковыми и равными 8.5
10 8 А / см2 . Считать уровни легирования p- и n-областей одинаковыми и равными 8.5  1015 см 3 .
1015 см 3 .
85

9. «ЭМИССИЯ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ ИЗ ПОЛУПРОВОДНИКОВ»
9.1. КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРИИ
Проблему изучения эмиссии излучения из твердых тел можно рассматривать с двух позиций: макроскопической и микроскопической, различающихся объектом рассмотрения излучающих свойств.
С макроскопической позиции излучательные свойства твердого тела анализируются как свойства однородного кристалла. Здесь для численной оценки эффективности излучательной способности вводят два параметра. Первый из них называется внутренней квантовой эффективностью . Он характеризует способность атомов полупроводника излучать фотоны при рекомбинации электронно-дырочных пар и вычисляется следующим образом:
1
|
|
l |
|
|
|
r |
(9.1) |
|
1 |
|
1 |
|
|
r l |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
l |
r |
|
|
|
|
|
т.е. это параметр превышения способности генерировать фотоны над способностью того же вещества генерировать фононы. Численно он определяет: сколько генерируется фотонов в результате рекомбинации одной пары «электрон-дырка». Как показывает расчет (см. п.6.2 Учебного пособия по курсу Давыдов В.Н. «Физические основы оптоэлектроники», Томск, ТУСУР, 2011 г.), для повышения внутренней квантовой эффективности источника оптического излучения для его изготовления необходимо использовать полупроводники с высоким уровнем легирования.
Для того чтобы наблюдать эмиссию излучения, необходимо, чтобы сгенерированные фотоны вышли из полупроводника через одну из его граней в окружающее пространство. Однако, распространяясь в кристалле на пути от места генерации к излучающей поверхности, фотоны могут быть поглощены другими атомами, находящимися в основном энергетическом состоянии. Поэтому вводят еще один па-
раметр, называемый внешней квантовой эффективностью и обо-
значаемый как . Он показывает долю сгенерированных в объеме полупроводника фотонов, вышедших через его поверхность:
86

ф |
, |
(9.2) |
ф L |
где L – толщина полупроводника в направлении на излучающую поверхность; ф – длина свободного пробега фотона в полупроводнике.
Из этого определения видно, что условие достижения высокого выхода светового излучения заключается в том, чтобы сгенерированные фотоны могли выйти из полупроводника не будучи поглощенными другими атомами на пути от излучающего атома до поверхности. Для этого необходимо, чтобы длина свободного пробега фотона была
больше толщины образца: ф 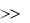 L .
L .
Конечно, эти два параметра не дают исчерпывающий ответ на вопрос об эффективности излучающей способности полупроводника. Кроме этих двух параметров можно ввести еще несколько, с помощью которых отображалось бы выполнение еще ряда условий, которые необходимо соблюсти для повышения эффективности излучения (например, условия на коэффициент отражения света от внутренней поверхности полупроводника). Но эти два – основные.
С микроскопической позиции излучающие способности твердого тела рассматриваются как результат излучения отдельных атомов, т.е. анализируются механизмы генерации излучения отдельным атомом. Детальный анализ показывает, что при этом подходе двумя параметрами, определяющими эффективность излучения отдельного атома, являются вероятности спонтанного - A21 и индуцированного - B21 переходов (см. п.6.3 учебного пособия Давыдова В.Н. Физические основы оптоэлектроники. Томск, ТУСУР, 2011 г.). Эти параметры определяются природой атома, его структурного состояния в решетке и потому являются константой для данного вещества. Следовательно, численные значения этих параметров можно найти в справочных материалах.
Для характеристики излучательной способности оптического излучения твердотельного лазера необходимо проверять выполнение двух условий:
- условие резонанса оптической волны на длине резонатора L :
L m |
|
, |
(9.3) |
2n |
87

где n - показатель преломления вещества, являющегося активным в лазере, m - целое число, показывающее количество полуволн оптического излучения, укладывающихся на длине кристалла; - условие значения коэффициента усиления активного вещества
g , достаточного для возникновения генерации, если кристалл помещен в оптический резонатор с зеркалами, коэффициенты отражения от которых равны R1, R2 , а коэффициент поглощения оптического излучения с генерируемой длиной волны в актив-
ном веществе лазера равен |
: |
|
|
|
|
g |
1 |
ln R R |
|
. |
(9.4) |
|
2 |
||||
|
2L |
1 |
|
|
|
|
|
|
|
|
Для получения генерации оптического излучения полупроводниковым лазером это условие сводится к необходимости задания протекающего тока через открытый p-n переход величиной выше порогового тока.
9.2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ОПРЕДЕЛЕНИЮ ПАРАМЕТРОВ ЭМИССИОННЫХ ЭФФЕКТОВ
В ПОЛУПРОВОДНИКАХ
Задача 1. Определить параметр внутренней квантовой эффективности генерации оптического излучения германиевого образца n ти-
па |
проводимости |
с |
концентрацией |
донорной |
примеси |
Nd |
2.4 1017 cм 3 , находящегося при температуре T 300 K . |
||||
|
Решение. Исходным |
выражением для |
определения |
параметра |
|
внутренней квантовой эффективности является выражение (9.1), в котором неизвестными величинами являются время жизни излучательной рекомбинации l и время жизни безизлучательной рекомбинации
r :
|
r |
|
. |
(9.5) |
|
|
|
||
r |
|
l |
|
|
Время жизни излучательной рекомбинации зависит от уровня легирования полупроводника по закону:
88

l |
(i ) |
2ni |
. |
(9.6) |
|
l |
n0 p0 |
||||
|
|
||||
|
|
|
|
Из табличных данных известно, что время излучательной рекомбина-
ции в собственном германии составляет |
(i ) |
0.6 c . Поэтому по вы- |
||||||||
l |
||||||||||
|
|
|
|
|
|
|
|
|
||
ражению (9.6) будем иметь: |
|
|
|
|
|
|||||
l |
(i ) 2n |
i |
|
0.6 |
2 2.4 1013 |
1.2 10 4 c . |
|
|||
l |
Nd |
|
2.4 1017 |
|
||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|||||
Из справочных материалов находим, что время жизни неравно- |
||||||||||
весных электронов и дырок германии составляет величину |
10 5 c . |
|||||||||
Это время определено как время жизни неравновесных носителей заряда при безизлучательной рекомбинации r . Значит, интересующий нас параметр внутренней квантовой эффективности процесса излучения может быть вычислен по формуле:
|
|
|
|
r |
|
. |
|
|
|
(9.7) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
l |
r |
|
|
|
|
||
Поэтому окончательно имеем: |
|
|
|
|
|
|
|
|
|||
|
r |
|
|
10 5 |
|
|
|
0.1 |
7.7 10 |
2. |
(9.8) |
|
l r 1.3 10 |
4 |
|
1.3 |
|||||||
|
|
|
|
|
|||||||
Таким образом, ответ на поставленный в задаче вопрос будет таким: параметр внутренней квантовой эффективности германиевого образца составляет 0.077 или 7.7% .
Задача 2. Вычислить параметр внешней квантовой эффективности кремниевого образца, изготовленного в виде куба и содержащего
Naт 1021 атомов, если излучение лежит в диапазоне собственного поглощения.
Решение. Исходным выражением для определения параметра внешней квантовой эффективности служит выражение (9.2), в котором стоят неизвестные величины длины свободного пробега фотонов и размера кристалла. Их можно определить следующим образом: по определению длина свободного пробега фотонов является величиной, обратной коэффициенту поглощения излучения: ф 1 . Линейные
89

размеры кристалла можно определить из количества атомов в образ-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
це: L 1 3 N |
|
. Следовательно, получим: |
|
|
|
|
|
|
|||||||||||||||||
|
|
ат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ф |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
ф |
L |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
Nат 1 / |
|
Naт |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
0.9. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 106 / 107 |
|
1 0.1 |
1.1 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Таким образом, ответ на вопрос о величине параметра внешней квантовой эффективности будет таков: внешняя квантовая эффективность образца кремния с заданным числом атомов в нем будет составлять около 90%.
Задача 3. Каким должен быть коэффициент усиления излучения
из области примесного поглощения |
(коэффициент поглощения |
103 см 1) в твердом теле длиной L |
2.5 10 5cм и торцами в виде |
отражающих зеркал, коэффициент отражения одного из них R1 1, если через второе зеркало выводится 5% генерируемого излучения.
Решение. Эта задача может быть решена с использованием выражения (9.4) при известных значениях коэффициента поглощения
излучения , обоих коэффициентов отражения зеркал R1, R2 и длины кристалла в направлении усиления света L :
g |
1 |
ln R R |
|
. |
|
2 |
|||
|
2L |
1 |
|
|
|
|
|
|
Из условия задачи следует, что коэффициент отражения света вторым зеркалом R2 0.95 . Поэтому с использованием формул разложения логарифма вблизи единичного значения аргумента получим:
g 103 |
|
|
1 |
|
ln 1 0.95 |
103 |
|
1 |
|
ln 1.0 0.05 |
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
5 |
|
|
|
5 |
||||||
|
|
|
5 10 |
|
|
5 10 |
|
|||||||
103 |
|
|
1 |
|
|
0.05 |
103 |
1 |
|
0.05 |
||||
|
|
|
|
|
|
|
|
|
||||||
5 |
|
10 |
5 |
|
5 10 |
5 |
||||||||
|
|
|
|
|
|
|
|
|||||||
103 |
5 |
|
103 |
2 103 cм 1. |
|
|
|
|
|
|
|
|||
5 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, |
коэффициент усиления твердого тела должен |
|||||||||||||
быть больше 2  103 cм 1.
103 cм 1.
90
