Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Теория информации.-1

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

3.28 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1714 15 16 17 > Следующая >>>

131
борочном значении y
I (1: 2; y) ln	m2	y	m2 m1	.

	m1		m1m2

В соответствии с критерием Неймана-Пирсона эту величину необходимо сравнить с порогом С и принять гипотезу Н1, если

выполняется неравенство		I (1: 2; y)		C . Отсюда область Е1
принятия гипотезы Н1 состоит из всех значений						y , удовлетво-
ряющих неравенству
y C ln	m2	m m (m m ) y .

	m1	1	2	2	1	0

Правая часть этого неравенства есть постоянная, которую
мы обозначили y0 , и, следовательно,				область Е1		состоит из всех
значений сигнала, для которых 0 y					y0 . Остальные значения

yy0 относим к области Е2 (см. рис. 5.1). Вероятность ошибки первого рода

W ( y)dy

exp(

)dy

exp(

)

exp(

Границу y0

необходимо выбрать так, чтобы обеспечить за-

данное значение

exp(

y0 / m1 )

0, 01832, отсюда

m1 ln 0, 01832

4m1

Итак, правило проверки гипотез формулируем следующим образом. Если случайная величина Y приняла в результате опыта значение 0 y 4, считаем, что математическое ожидание

этой величины m m1 1. В противном случае считаем, что

m m2 10.

б) Вычислим вероятность ошибки второго рода

y0		y0
W2 ( y)dy	(1 m2 )	exp(	y m2 ) dy
1 0exp( y0	m2 ) 1	0exp(	0, 4) 0,3297.

в) Наконец, определим, возможно ли в принципе обеспе-

132

чить α=β=0,1. По формуле (5.1.2) вычисляем

I (1: 2)

exp

m1m2

ln10

0,9

1, 4026.

m m

Правая часть неравенства (5.1.9 а) равна

) ln

0,1 ln

0,1

0,9 ln

0,9

1, 7578.

0,9

0,1

Требуемые значения α=β=0,1 не удовлетворяют уже первому из неравенств (5.1.9), следовательно, не существует правило проверки гипотез, которое обеспечивало бы такие значения вероятностей ошибок первого и второго рода.

Пример 5.1.3. В условиях примера 1.3 вычислить для гипотез:

H1 – сообщение на входе x(t)=x1(t); H2– сообщение на входе x(t)=x2(t),

где x1(t) и x2(t) – известные наблюдателю функции. Найти предельное выражение для I(1:2) при условии, что верхняя граничная частота шума Fв стремится к бесконечности, а полоса сигнала x(t) остается неизменной.

Решение. Совместные плотности вероятности n отсчетов квантованного сигнала при каждой из гипотез равны (см. при-

мер 1.3):

y(1)

,..., y(n)

exp

( y

2 N0 Fв

2N0 Fв

k 1

y(1)

,..., y(n)

exp

( y

2 N0 Fв

2N0 Fв

k 1

где

x (k )

x (t

) ,

x (k )

x (t

) .

1 k

2 k

(k ) x1(k ) )2 ,

(k ) x2(k ) )2 ,

Случайные величины Y(1),…,Y(n) независимы при каждой из гипотез, следовательно, для вычисления I(1:2) можно воспользоваться свойством аддитивности информации

133

I (1:2)=

Ik (1:2) ,

k =1

W y(k )

/ x(k )

где

(1:2)=

W y(k ) / x(k )

dy(k ) .

W y(k )

/ x(k )

В примере 5.1.1 было установлено, что

x1(k )

x2(k )

(m m )

Ik (1:2)=

0 в

и окончательно получаем

I (1:2)=

x(k )

2N0 Fв k 1

Вычислим предельное значение средней информации для

различения в пользу H1

против H2

при Fв

t 0

(1:2)= lim

x(k )

k 1 2N0 Fв

Внесем множитель

1 (2Fв ) под знак суммы и заметим,

что ее пределом является определенный интеграл, вычисленный на интервале (0,T)

) 2

I (1:2)=

lim

x (t

)

x (t

k 1

x (t)

dt.

Таким образом, величина средней информации для различения двух сообщений известной формы на фоне аддитивного белого шума зависит только от интенсивности шума и от квадрата расстояния между этими двумя сообщениями (сравните с результатами примера 5.1.1).

5.2 Информация по Фишеру

Определение. Свойства. Пусть сообщение X есть непре-

I(x1:x2)

134

рывная случайная величина, а сигнал y y(1) ,..., y(n) характери-

зуется условной плотностью вероятности W ( y(1) ,..., y(n) / x). Рассмотрим две гипотезы:

H1	– передано сообщение x1, то есть W			W ( y(1) ,..., y(n) / x ) ,
			1	1
H2	– передано сообщение x2, то есть W			W ( y(1) ,..., y(n) / x ) .
			2	2
	Среднюю информацию в пользу H1, вычисленную по фор-
муле (5.1.2)
	I (1: 2)	... W ( y(1) ,..., y(n) / x )
			1
				(5.2.1)
		W ( y(1) ,..., y(n) / x )	dy(1)	,..., dy(n) ,
	log	1
	log	W ( y(1) ,..., y(n) / x )
		W ( y(1) ,..., y(n) / x )
		2

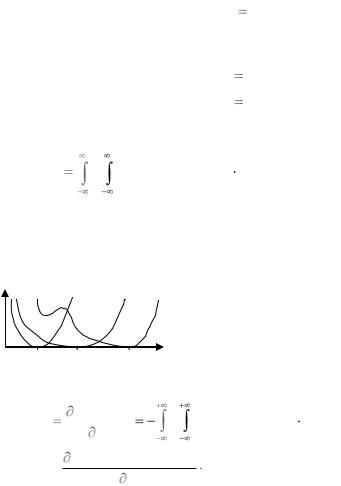
можно формально рассматривать как функцию аргумента x2, зависящую от параметра x1. На рис.5.2 в качестве примера приприведен возможный вид этой

							функции при различных значе-
							ниях x1.
		x1'		x1''	x1'''	x2	Если существует вторая
			Рис. 5.2				производная этой функции по
							x2 в точке x2= x1= x,
				2 I (x : x )			W ( y[1] ,..., y[n] / x)
I		(x)		1	2	...
I	F	(x)		x2		...
	F			x2			(5.2.2)
			2				(5.2.2)
			2

2lnW ( y[1] ,..., y[n] / x) dy[1]...dy[n].

то ее величина называется информацией по Фишеру о параметре x, содержащейся в сигнале y.

То же значение информации можно получить в результате вычисления по формуле

135

I	F	(x)	... W ( y[1] ,..., y[n] / x)
	F
				(5.2.3)
			lnW ( y[1] ,..., y[n] / x)	2
				dy[1]...dy[n].
			x	dy[1]...dy[n].
			x

Выбор одной из двух формул определяется только удобством вычислений. Информация Фишера показывает, насколько


быстро		возрастает		функция	I(x1:x2) при увеличении
x	x1	x2	и, следовательно,		является мерой различимости
близких значений x1				и x2.

Информация Фишера, как и информация Кульбака, обладает свойствами выпуклости и аддитивности. Единицы измерения информации Фишера – это единицы измерения величины х-2.

Неравенство Рао-Крамера. Это – главный результат теории информации по Фишеру.

Рассмотрим задачу оценки непрерывного сообщения x. Правило оценивания сводится к тому, что каждому значению

выборки y y(1) ,..., y(n) ставится в соответствие некоторое значение оцениваемого параметра x. Таким образом, оценка xˆ( y(1) ,..., y(n) ) является функцией выборочных данных и поэто-

му также является случайной величиной. Обычно вычисляют следующие числовые характеристики оценки:

1) Математическое ожидание при условии, что истинное значение сообщения равно x,

m(x)	... xˆ( y[1] ,..., y[n] ) W ( y[1] ,..., y[n] / x)	dy[1]...dy[ n].	(5.2.4)
			(5.2.4)
2) Смещение
	b(x) m(x) x,		(5.2.5)

т.е. систематическую ошибку, сопутствующую выбранному правилу оценивания.

3) Дисперсию, вычисляемую также при условии, что истинное значение сообщения равно x,

136

D(x)	... xˆ( y[1] ,..., y[n] ) m(x) 2	(5.2.6)
W ( y[1] ,..., y[n] / x) dy[1]...dy[n].

Дисперсия оценки является основной количественной мерой точности оценивания.

Пусть функция правдоподобия W ( y(1) ,..., y(n) / x) диффе-

ренцируема по параметру x, информация Фишера (5.2.2) существует и не равна нулю для всех значений параметра в окрестности точки x, тогда дисперсия и смещение любой оценки связаны с информацией Фишера неравенством Рао-Крамера

1		db(x)		2
				(5.2.7)
			dx
D(x)					.
	IF		(x)

Для несмещенных оценок (b(x)=0) или для оценок с постоянным, не зависящим от x смещением (b(x)=c), числитель в (5.2.7) равен единице и тогда

D(x)	1	.
			(5.2.8)
	IF (x)

Таким образом, информация Фишера является количественной мерой предельной, потенциальной точности оценивания непрерывного сообщения x, так как дисперсия несмещенной оценки не может быть меньше величины, обратной информации Фишера.

Неравенства (5.2.7) и (5.2.8) обращаются в равенства тогда

итолько тогда, когда одновременно выполняются два условия:

1)Функция правдоподобия выборки может быть представлена в виде

W ( y

[1]

,..., y

[n]

/ x)

h y

[1]

,..., y

[n]

f xˆ y

[1]

,..., y

[n]

, x ,

(5.2.9)

где h y[1] ,..., y[n]

– некоторая функция выборки

y, не завися-

щая от x и xˆ ,

f xˆ, x

– функция, зависящая только от x и xˆ

y[1] ,..., y[ n] .

137

Оценка xˆ y[1] ,..., y[n] , удовлетворяющая условию (5.2.9), на-

зывается достаточной, поскольку она сохраняет всю информацию о x, содержащуюся в самой выборке.

2) Функция правдоподобия выборки такова, что для любого x выполняется соотношение

	lnW ( y[1] ,..., y[n] / x)	k(x) xˆ y[1] ,..., y[n] m(x) ,	(5.2.10)
	x


где k(x) – некоторая функция x.

Оценка, удовлетворяющая этому уравнению, называется эффективной, а семейство распределений, задаваемых уравнением (5.2.10) при различных значениях x, называется экспоненциальным семейством. Легко убедиться, что эффективная оценка всегда достаточна, но обратное утверждение неверно.

Среди всех оценок с заданным смещением именно эффективные оценки обладают минимальной дисперсией. К сожалению, эффективная оценка существует далеко не во всех случаях, и тогда потенциальная точность оценивания сообщения недостижима.

Оценка максимального правдоподобия. Метод макси-

мального правдоподобия широко используется на практике. В качестве оценки xˆ y[1] ,..., y[n] выбирается такое значение x,

при котором функция правдоподобия W ( y[1] ,..., y[n] / x) дости-

гает наибольшего значения. Это значит, что в качестве оценки максимального правдоподобия выбирается решение уравнения правдоподобия

W ( y[1] ,..., y[n] / x)	0 или	lnW ( y[1] ,..., y[n] / x)	0.	(5.2.11)
x		x

Доказано, что если эффективная оценка существует, то она может быть реализована методом максимального правдоподобия.

РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ

Пример 5.2.1. Случайная величина Y имеет экспоненциальное распределение

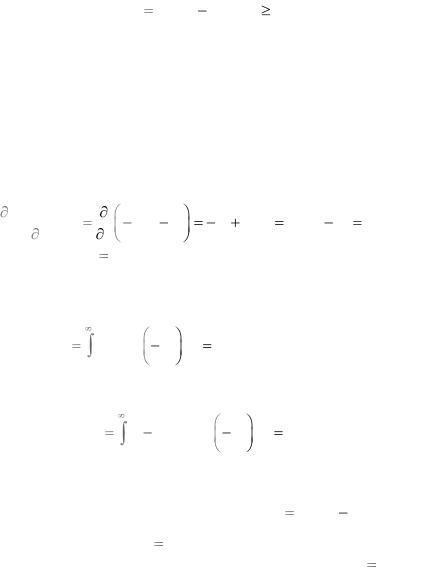
	138
W ( y / x)	1	exp(	y	), y 0 .

	x		x

а) Найти максимально правдоподобную оценку математического ожидания m этой случайной величины.

б) Найти статистические характеристики (математическое ожидание и дисперсию) этой оценки.

в) Определить, является ли оценка достаточной. г) Определить, является ли оценка эффективной.

д) Найти информацию Фишера и по неравенству Рао-Кра- мера проверить сделанное заключение об эффективности оценки.

Решение. Запишем уравнение правдоподобия

lnW ( y / x)

ln x

( y x) 0.

Отсюда xˆ( y)

y , т.е. максимально правдоподобная оценка

математического ожидания равна наблюдаемому выборочному значению y .

По формуле (5.2.4) находим математическое ожидание

оценки m(x)

exp

x .

Таким образом, оценка xˆ( y) является несмещенной.

Дисперсию оценки вычисляем по формуле (5.2.5)

D(x)

[ y

exp

Для того чтобы определить, является ли оценка достаточной, сравним функцию правдоподобия с выражением (5.2.9).

Видим, что h(y)= 1, а функция f [xˆ( y), x]	1	exp(	y	) за-

	x		x

висит только от x и xˆ( y) y . Функция правдоподобия выборки может быть представлена в форме (5.2.9), и оценка xˆ( y) y

является достаточной.

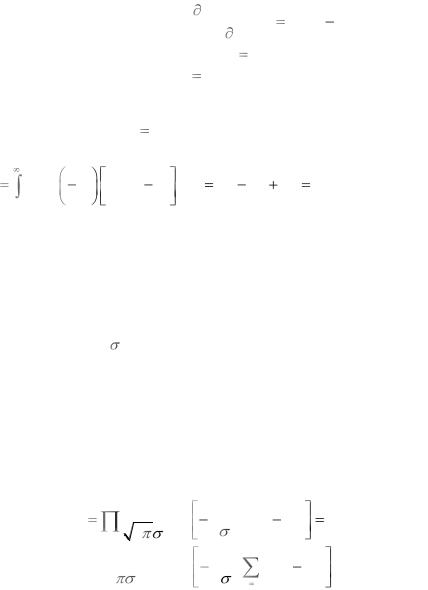
139

Полученное ранее выражение	lnW ( y / x)	1		( y x)

	x		x2
сравним с выражением (5.2.10). Полагая k (x) 1/ x2		и подстав-
ляя полученные нами выражения xˆ( y)	y и m(x)=x, видим, что

производная от логарифма функции правдоподобия может быть представлена в виде (5.2.10), и, следовательно, оценка макси-

мального правдоподобия xˆ( y)								y является эффективной.
Информацию Фишера находим по формуле (5.2.3)
		1		y	1			2	2	2		1		1
IF (x)		1	exp	y	1		( y	x) dy	2	2		1		1	.

	0	x		x		x2			x2		x2		x2	x2
	0

Видим, что неравенство Рао-Крамера (5.2.8) обращается в равенство. Этого и следовало ожидать, так как мы уже показали, что оценка эффективна. Лучшей оценки, т.е. обладающей меньшей дисперсией при отсутствии систематической ошибки, не существует.

Пример 5.2.2. Система независимых случайных величин

Y (1) ,...,Y (n) распределена нормально с одинаковым среднеквад-

ратическим отклонением и одинаковым, но неизвестным математическим ожиданием x.

а) Найти выражение для максимально правдоподобной оценки математического ожидания x .

б) Найти смещение и дисперсию этой оценки.

в) Определить потенциальную точность оценки величины

математического ожидания x .
Решение. Функция правдоподобия						выборки			y(1) ,..., y(n)
равна
	n	1			1
W ( y(1) ,..., y(n) / x)		1		exp	1			( y(k )	x)2
					2		2
		2
	k =1	2
		1			1			n
		1		exp	1			( y(k ) x)2 .

(2			2 )n / 2		2		2
(2			2 )n / 2		2		2	k 1

Запишем уравнение правдоподобия и преобразуем его к удобному виду

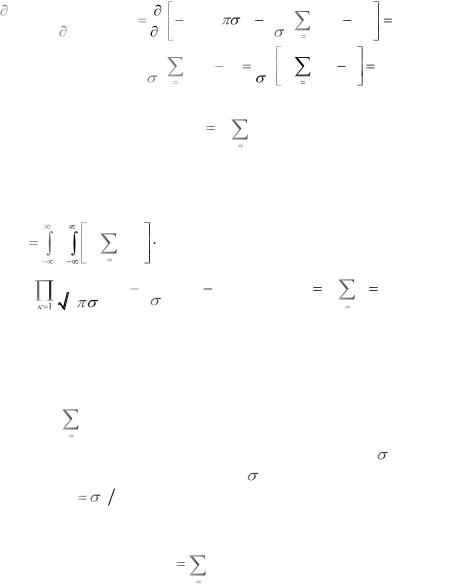
140

lnW ( y(1) ,...., y(n) / x)

ln(2

2 )

( y(k )

x)2

1 n

( y(k ) x)

y(k )

x 0.

n k

k 1

Решением уравнения является значение

1 n

xˆ( y(1)

,..., y

(n) )

y( k ) .

n k

Таким образом, максимально правдоподобная оценка математического ожидания х равна выборочному среднему.

По формуле (5.2.4) найдем математическое ожидание самой оценки

		1			n
m(x)	...				y(k )
m(x)	...				y(k )
			n k 1
n		1			exp[	1	( y(k )	x)2 ]dy(1) ...dy(n)	1 n	x x,
						2

		2		2					n k	1

так как математическое ожидание суммы случайных величин равно сумме математических ожиданий. Таким образом, смещение оценки равно нулю.

Дисперсия оценки может быть найдена непосредственно по формуле (5.2.6) либо же следующим, более простым способом.

Величина y(k ) является суммой n независимых случайных

k 1

величин, причем дисперсия каждого из слагаемых равна 2 . Тогда дисперсия этой суммы равна n 2 , и тогда дисперсия

оценки D(x)

2 n.

Вычисление информации Фишера, содержащейся в выборке, удобно произвести с использованием свойства аддитивности

	n
IF (x)	IF (x)k ,
k	1

где

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1714 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20232.33 Mб24Теория игр..pdf
#
05.02.2023286.13 Кб0Теория инноваций..pdf
#
05.02.2023435.94 Кб8Теория информации и информационных систем.-1.pdf
#
05.02.2023254.64 Кб12Теория информации и информационных систем.-2.pdf
#
05.02.2023295.6 Кб13Теория информации и информационных систем..pdf
#
05.02.20233.28 Mб15Теория информации.-1.pdf
#
05.02.2023196.85 Кб12Теория информации.-2.pdf
#
05.02.2023339.94 Кб14Теория информации.-3.pdf
#
05.02.2023440.95 Кб12Теория информации.-4.pdf
#
05.02.2023271.66 Кб9Теория информации.-5.pdf
#
05.02.2023573.08 Кб23Теория информации..pdf