Теория информации.-1

111

Первая и вторая теоремы. Если скорость создания информации Н источником на входе шумящего канала без памяти с пропускной способностью С меньше пропускной способности, то существует такой код, при котором вероятность ошибок на приемном конце сколь угодно мала, а скорость передачи информации сколь угодно близка к скорости ее создания.

Обратная теорема. Если Н > С, то никакой код не сможет сделать вероятность ошибок сколь угодно малой и достигнуть ненадежности, меньшей чем Н-С.

Основной способ повышения помехоустойчивости системы передачи информации – это разумное введение избыточности в передаваемый сигнал А(t).

Корректирующие коды. Идея рационального введения избыточности в передаваемый сигнал для борьбы с ошибками в каналах с шумами реализуется применением корректирующих кодов. Так называются коды, которые позволяют обнаруживать

идаже исправлять ошибки, возникающие в канале. Наиболее часто применяют двоичные равномерные корректирующие коды.

Пусть а1, а2, ... , аs – двоичные кодовые слова длиной в n символов каждое, соответствующие s буквам алфавита источника. Каждое кодовое слово можно формально рассматривать как вектор-строку, соответствующий некоторой точке в n-мерном пространстве.

Расстояние Хэмминга djk между двумя кодовыми словами аj

иаk равно числу символов, в которых эти слова отличаются одно от другого.

Удобно вычислять расстояние между двумя кодовыми словами, пользуясь операцией суммирования по модулю 2. Правила

эквивалентны.

Расстояние между двумя кодовыми словами можно теперь определить как количество единиц в кодовом слове, полученном при суммировании этих слов по модулю 2.

112

Наименьшее значение расстояния между словами в выбранной системе кодирования называется кодовым расстоянием

dкод.

Считают, что в канале произошла q-кратная ошибка, если кодовое слово на выходе канала отличается от кодового слова на его входе ровно в q символах (т.е. расстояние между этими словами-векторами равно q). Таким образом, вектор на выходе канала равен сумме по модулю 2 входного вектора и вектора ошибки.

Код позволяет обнаруживать любую ошибку кратности qо, если его кодовое расстояние удовлетворяет условию

Код позволяет исправлять любую ошибку кратности qи, если выполняется условие

Линейные блочные коды. Среди всех корректирующих кодов наибольшее применение нашли линейные блочные коды. Это – двоичный корректирующий (n,k)-код, удовлетворяющий следующим требованиям:

1) Все кодовые слова содержат по n символов, из которых k символов – информационные, а остальные n-k символов – проверочные.

2) Сумма по модулю 2 любых двух кодовых слов снова дает кодовое слово, принадлежащее этому же коду.

Линейный блочный код код задается производящей матрицей G, имеющей k строк и n столбцов. Строки производящей матрицы должны быть линейно независимыми, т.е. сумма любых строк (по 2, по 3 и т.д. в любых комбинациях) не должна давать нулевое слово (состоящее из одних нулей).

Следующим этапом в построении линейного блочного кода является определение проверочной матрицы Н, имеющей r=n-k строк и n столбцов. Любой вектор-строка проверочной матрицы Н ортогонален любому вектору-строке производящей матрицы G, следовательно,

где HT – транспонированная матрица H.

113

Заметим, что два вектора u=u1,...,un и v=v1,...,vn являются, по определению, ортогональными, если

uv u1v1 u2v2 ... unvn 0 .

Работа кодера для (n,k)-кода заключается в том, что к поступающему на его вход k-разрядному вектору информационных символов x он должен добавить r проверочных символов. Правило образования кодового слова а определяется соотношением

Умножив обе части этого выражения справа на HT и учитывая (4.3.3), получим другое соотношение, определяющее функции кодера

т.е. он должен добавлять r проверочных символов таким образом, чтобы любой из получаемых в итоге кодовых векторов а удовлетворял соотношению (4.3.5).

Один из способов декодирования принятого вектора b предусматривает вычисление r-разрядного исправляющего вектора (синдрома) с по правилу

Из формулы (4.3.5) следует, что значение синдрома определяется только вектором ошибки. Если с 0, делают заключение о наличии ошибки (обнаружение ошибки). Так как различным ошибкам кратности qи, удовлетворяющей неравенству (4.3.2), соответствуют различные значения синдрома, то вычисленное значение синдрома с однозначно определяет положение символов, в которых произошли такие ошибки. Эти ошибки исправляются в декодере суммированием принятого вектора b с соответствующим вектором ошибок.

Основными элементами кодирующих и декодирующих устройств для систематических кодов являются сумматоры по модулю 2 и сдвигающие регистры. Сдвигающим регистром называют цепочку, состоящую из двоичных ячеек (в дальнейшем они изображаются прямоугольниками), меняющую свое состояние в дискретные моменты времени (шагами). На каждом шаге двоичный символ, имеющийся на входе ячейки, перемещается на ее

114

выход.

Ниже приведены краткие данные наиболее распространенных систематических кодов.

Код Хэмминга имеет кодовое расстояние, равное трем, и полностью характеризуется числом проверочных символов r. Общее число символов в кодовом слове равно n=2r-1. В качестве столбцов проверочной матрицы Н выбираются всевозможные r- разрядные двоичные числа, исключая число нуль.

Код Рида-Малера полностью характеризуется двумя целыми положительными числами: m≥З и δ<m. Число δ называется порядком кода. Остальные параметры кода определяются из соотношений:

Первая строка производящей матрицы G состоит из единиц. Следующие m строк (базисные векторы первого порядка) можно получить, если записать n столбцов, состоящих из m-разрядных

двоичных чисел. Следующие Cm2 строк (базисные векторы вто-

рого порядка) получают, вычисляя поэлементные произведения различных пар базисных векторов первого порядка, и т.д. до получения базисных векторов δ-го порядка.

Циклический код полностью определяется первой строкой производящей матрицы G. Остальные строки получают в результате циклического сдвига первой строки на 1,2,...,k-1 элементов. Таким же циклическим свойством обладает и проверочная матрица Н.

Более удобным является общепринятое описание кодовых комбинаций циклического кода при помощи полиномов. Кодовой комбинации v=(v0,v1,…,vn-1) соответствует полином

v(x)= v0x0+ v1x1+,…,vn-1xn-1. Способы кодирования и декодирова-

ния для конкретного кода полностью определяются, если задать производящий полином g(x)=1+g1x+ g2x2+…+ gr-1xr-1+xr.

Фундаментальное свойство циклического кода заключается в том, что полином, соответствующий любой разрешенной (передаваемой) кодовой комбинации, делится без остатка на производящий полином.

115

РЕШЕНИЕ ТИПОВЫХ, ПРИМЕРОВ Пример 4.3.1. Способ кодирования задан кодовой табли-

цей

Следовательно, приведенный код позволяет обнаруживать всевозможные однократные, двукратные и трехкратные ошибки и исправлять любые однократные ошибки.

г) Избыточность кода находим из следующих соображений. Для передачи равновероятных сигналов a1, а2, а3, а4 достаточно передавать кодовые слова 00, 10, 01 и 11 соответственно. Такой код не имеет избыточности, но не позволяет обнаруживать и, тем более, исправлять ошибки. Для обнаружения и исправления ошибок введены пять избыточных символов, т.е. количественно

избыточность равна R (7 2)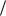7 71% .

Пример 4.3.2. Линейный блочный (5,2)-код задан производящей матрицей в систематической (канонической) форме

116

Произвести декодирование следующими методами: а) по минимуму расстояния; б) вычислением синдрома.

Решение. Если производящая матрица записана в каноническом виде, это значит, что она состоит из двух блоков: диагональной матрицы размера k k, состоящей из единиц, и прямоугольной матрицы размера r k. В этом случае первые k символов в любом кодовом слове являются информационными.

Проверочная матрица Н также может быть записана в каноническом виде и состоит из двух блоков. Первый блок есть прямоугольная матрица размера k r, полученная транспонированием второго блока матрицы G. В качестве второго блока матрицы Н записывают диагональную матрицу размера r r, состоящую из единиц.

Для заданного кода получаем

10100

Н11010 .

01001

Убедимся, что полученная таким образом матрица Н удовлетворяет соотношению (4.3.3). Действительно,

h1g1 (10100) (10110) 0, h1g2 (10100) (01011) 0,

............................................

h3g2 (01001) (01011) 0,

т.е. все 6 элементов матрицы GHT равны нулю.

Построим кодовую таблицу, воспользовавшись правилом образования кодовых слов по формуле (4.3.4):

a1=00000, а2=10110, а3=01011, а4=11101=a2+a3.

Всего кодовая таблица содержит 2k = 4 вектора.

Из кодовой таблицы определяем величину кодового расстояния dкод 3 .

Следовательно, рассматриваемый код обнаруживает однократные и двукратные ошибки и исправляет однократные.

Декодируем принятый вектор b = 00110.

а) Метод декодирования по минимуму расстояния заклю-

119

лицу

0000 0000000, 0001 0001111,...,1111 1111111.

Пример 4.3.5. Для кода Хэмминга, определяемого прове-

рочной матрицей H, построенного в примере 4.3.4, декодировать принятый вектор 1011001.

Решение. Для принятого вектора b=1011001 по формуле (4.3.6) вычисляем синдром

Синдром с≠0, т.е. имеет место ошибка. В случае одиночной ошибки (и только лишь) вычисленное значение синдрома всегда совпадает с одним из столбцов матрицы Н, причем номер столбца указывает номер искаженного символа. Видим, что ошибка произошла в первом символе и передавался вектор

a0011001.

ЗАДАЧИ

4.3.1. Составить кодовую таблицу, определить кодовое расстояние и вычислить минимальное значение избыточности 3-разрядного двоичного кода, удовлетворяющего требованиям:

а) код содержит максимальное количество кодовых слов; б) код обнаруживает все однократные ошибки; в) код исправляет все однократные ошибки.

Построить геометрические модели полученных кодов.

4.3.2.Дать правило построения простейшего кода, обнаруживающего все ошибки нечетной кратности.

4.3.3.Показать, что векторы

V1 = 10111, V2 = 01011,V3 - = 01110

линейно независимы, а векторы

U1=10001, U2=10011, U3=0110

ортогональны векторам VI.

4.3.4. Найти все кодовые векторы для линейного блочного кода, заданного порождающей матрицей