
Теория автоматического управления.-2
.pdf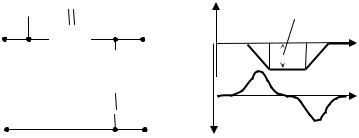
90
вательно включенным безынерционным усилителем, компенсирующим упомянутое ослабление коэффициента передачи (штриховая линия на рис. 6.5.2, б). Демпфирование системы этим методом основано на введении положительного фазового сдвига вблизи частоты среза исходной нескорректированной системы. Так как максимальный положительный фазовый сдвиг происходит на частоте, равной среднеарифметическому сопрягающих частот ω1 и ω2 (рис. 6.5.2, б), то именно эта частота должна равняться частоте среза исходной системы. Меняя сопрягающие частоты ω1 и ω2 , можно добиться заданных запасов устойчивости по амплитуде и по фазе.
В третьем методе демпфирования применяется пассивное интегро-дифференцирующее звено, реализация которого на RC- элементах приведена на рис. 6.5.3, а.
|
|
C1 |
|
|
|
|
|
20lgA(ω) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
ω1 ω2 ω3 ω4 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
lgω |
|||
|
|
R1 R2 |
|
|
−π/2 |
|
|
|
||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
Uвх |
|
|
Uвых |
|
|
|
||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
lgω |
|
|
|
|
C2 |
|
|
|
|
||||
|
|
|
|
|
|
φ(ω) |
|
|
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
а |
|
|
|
|
|
|
б |
|
Рис. 6.5.3. Пассивное интегро-дифференцирующее звено
Логарифмические характеристики, приведенные на рис. 6.5.3, б, показывают ослабление средних частот, а вносимый
91
фазовый сдвиг вначале отрицательный, а затем положительный. В соответствии с этим параметры RC-цепочки выбираются таким образом, чтобы частота среза исходной системы была бы близка к сопрягающей частоте ω3, но не превышала её. Величина уменьшения коэффициента передачи на частоте среза определяется требуемым запасом устойчивости по амплитуде.
Исходные данные к работе приведены в табл. 6.5.1. Таблица 6.5.1
№ |
T1 |
T2 |
∆L, дБ |
∆φ, град. |
K |
вари- |
|
|
|
|
|
анта |
|
|
|
|
|
1 |
0.2 |
0.5 |
10 |
15 |
10 |
2 |
0.3 |
0.2 |
12 |
20 |
7 |
3 |
0.2 |
0.4 |
8 |
12 |
6 |
4 |
0.1 |
0.2 |
12 |
10 |
12 |
5 |
0.3 |
0.5 |
10 |
20 |
6 |
6 |
0.1 |
0.5 |
7 |
15 |
7 |
7 |
0.4 |
0.6 |
8 |
20 |
9 |
8 |
0.3 |
0.6 |
12 |
15 |
11 |
9 |
0.2 |
0.3 |
9 |
20 |
10 |
10 |
0.2 |
0.7 |
8 |
18 |
8 |
11 |
0.4 |
0.1 |
11 |
15 |
8 |
12 |
0.3 |
0.6 |
9 |
15 |
9 |
13 |
0.1 |
0.3 |
10 |
15 |
15 |
14 |
0.5 |
0.6 |
8 |
20 |
7 |
15 |
0.1 |
0.1 |
12 |
15 |
9 |
16 |
0.3 |
0.1 |
10 |
20 |
10 |
17 |
0.2 |
0.5 |
8 |
20 |
8 |
18 |
0.4 |
0.2 |
12 |
15 |
11 |
19 |
0.3 |
0.3 |
11 |
25 |
13 |
20 |
0.1 |
0.5 |
13 |
10 |
14 |

92
6.5.3Порядок работы
1.Выбрать параметр А в передаточной функции разомкнутой системы (6.5.1) из условия нахождения замкнутой системы на границе устойчивости (согласно любому критерию устойчивости) и построить логарифмические частотные характеристики разомкнутой системы2.
2.Рассчитать передаточную функцию пассивного интегрирующего звена (рис. 6.5.1, а) и получить выражения для сопрягающих частот ω1 и ω2 через параметры элементов RC-цепочки.
3.Рассчитать необходимые значения сопрягающих частот ω1 и ω2 (рис. 6.5.1, б), исходя из частоты среза, полученной по результатам п.1, и заданного запаса устойчивости по амплитуде.
4.На основе результатов п.п. 2,3 рассчитать параметры R- и
C-элементов электрической цепи (рис. 6.5.1, а).
5.Построить логарифмические частотные характеристики разомкнутой скорректированной системы и определить запасы устойчивости полученной системы. Если полученные запасы устойчивости меньше заданных, скорректировать значения сопрягающих частот ω1 и ω2 и вернуться к п. 4.
6.Построить переходной процесс при единичном ступенчатом сигнале на входе замкнутой системы и измерить показатели качества – величину перерегулирования и время переходного процесса.
2 Все вычисления и построения можно выполнять с использованием любой из программ – MathCAD, MatLAB, SIMULINK, Mathematica, VisSim и др.
93
7.Рассчитать передаточную функцию пассивного дифференцирующего звена (рис. 6.5.2, а) и получить выражения для сопрягающих частот ω1 и ω2 через параметры элементов RC- цепочки.
8.Рассчитать необходимые значения сопрягающих частот ω1 и ω2 (рис. 6.5.2, б), исходя из частоты среза, полученной по результатам п.1.
9.Выполнить п.п. 4 − 6 для пассивного дифференцирующего
звена.
10.Рассчитать передаточную функцию пассивного интегродифференцирующего звена (рис. 6.5.3, а) и получить выражения для сопрягающих частот ω1, ω2, ω3 и ω4 через параметры элементов RC-цепочки.
11.Выполнить п.п. 4 − 6 для пассивного интегро-дифферен- цирующего звена.
6.5.4Содержание отчета
В отчете необходимо привести задание на выполнение работы, для каждого из вариантов коррекции: передаточные функции корректирующего звена; выражения для сопрягающих частот через параметры RC-схемы; логарифмические частотные характеристики исходной системы, корректирующего звена, системы с коррекцией; переходной процесс скорректированной системы; показатели качества скорректированной системы; сделать выводы. При защите работы устно ответить на вопросы.
94
6.5.5Вопросы
1.Перечислите основные методы демпфирования САУ.
2.Что такое частота среза?
3.Как определить запас устойчивости по амплитуде?
4.Как определить запас устойчивости по фазе?
5.Какой максимальный фазовый сдвиг дает пассивное дифференцирующее звено?
6.Какие недостатки у метода коррекции с помощью пассивного интегрирующего звена?
7.Какие недостатки у метода коррекции с помощью пассивного дифференцирующего звена?
8.Какую RC-цепочку нельзя применять для коррекции без соответствующего усилителя и почему?
6.6 Лабораторная работа №5. Анализ нелинейной
системы методом фазовой плоскости
6.6.1 Цель работы
Построить фазовый портрет и определить устойчивость движения нелинейной системы управления спутником, а также установить параметры предельного цикла, если таковой существует.
6.6.2 Основные соотношения
Функциональная схема системы стабилизации спутника по угловому положению представлена на рис. 6.6.1.

|
|
|
95 |
|||||
|
|
|
|
u1 |
||||
|
|
v |
Д1 |
|||||
|
|
|
|
|
|
|
||
ИСЗ |
vɺ |
|
|
u |
УУ |
|
||
|
||||||||
|
|
|
|
|||||
|
|
|
Д2 |
u2 |
|
|
|
|
|
M |
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 6.6.1. Схема системы регулирования |
||||||||
На рисунке показано: ИСЗ – искусственный спутник Земли (регулируемый объект), Д1 и Д2 – датчики угла рассогласования
v и угловой скорости vɺ соответственно, УУ – устройство
управления (регулятор совместно с исполнительным органом), u1 и u2 – напряжения на выходе датчиков, M – стабилизирующий момент, поворачивающий спутник в нужном направлении.
Задан вращающий момент инерции J (Г см с2), максимальное значение стабилизирующего вращающего момента M0
(Г см), датчик угла рассогласования имеет линейную статическую характеристику с коэффициентом передачи k1=1 в/град, статическая характеристика датчика угловой скорости приведе-
на на рис. 6.6.2, а, а характеристика регулятора – на рис. 6.6.2, б.
|
u2 |
|
|
|
M |
|
|
||
|
|
|
|
|
|
|
|||
−d |
α=arctgk2 |
−b |
|
|
M0 |
||||
|
|
|
|
|
|
|
|
|
|
|
d |
vɺ |
M0 |
b |
u |
||||
|
k2=1 в сек/град |
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
а |
|
|
|
б |
|
|
||
|
Рис. 6.6.2. Нелинейные характеристики |
|
|
|
|
||||
96
Исполнительный орган – газовый реактивный двигатель – имеет задержку во времени τ между моментом поступления входного воздействия u и моментом появления вращающего момента M. Для упрощения математической модели полагаем, что угловая скорость vɺ в течение этого времени τ постоянна.
Уравнение динамики объекта, согласно второму закону Ньютона и пренебрегая сопротивлением атмосферы
J |
d2v |
= −M . |
(6.6.1) |
|
dt2 |
||||
|
|
|
Сигнал на входе регулятора равен в соответствии с рис. 6.6.1 и характеристикой на рис. 6.6.2, а
|
|
|
k v |
|
|
|
|
|
при |
|
vɺ |
|
≤ d , |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
u = u1 |
|
1 |
|
|
|
(vɺ− d) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
+ u2 = k1v + k2 |
при vɺ > d , |
|
(6.6.2) |
||||||||||||||||
|
|
|
k v |
+ k |
|
|
(vɺ+ d) |
при vɺ < d. |
|
|
|
|||||||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Исходные данные приведены в табл. 6.6.1. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.6.1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
№ варианта |
|
J |
|
M0 |
|
|
τ |
|
b |
|
|
d |
|
v(0) |
vɺ(0) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
5000 |
|
400 |
|
|
0,2 |
|
0,1 |
|
0,1 |
|
0,5 |
-0,5 |
|
||||
|
2 |
|
5000 |
|
600 |
|
|
0,2 |
|
0,1 |
|
0,2 |
|
0,6 |
0 |
|
||||
|
3 |
|
7000 |
|
400 |
|
|
0,4 |
|
0,1 |
|
0,3 |
|
0,3 |
-0,5 |
|
||||
|
4 |
|
6000 |
|
500 |
|
|
0,3 |
|
0,2 |
|
0,4 |
|
0 |
0,6 |
|
||||
|
5 |
|
4000 |
|
600 |
|
|
0.3 |
|
0,3 |
|
0,2 |
|
-0,5 |
0,3 |
|
||||
|
6 |
|
4000 |
|
500 |
|
|
0,2 |
|
0,4 |
|
0,2 |
|
0,6 |
0,5 |
|
||||
|
7 |
|
5000 |
|
300 |
|
|
0,3 |
|
0,2 |
|
0,2 |
|
-0,5 |
0,6 |
|
||||

97
8 |
7000 |
600 |
0,4 |
0,1 |
0,4 |
-0,6 |
-0,4 |
9 |
4000 |
500 |
0,5 |
0,3 |
0,2 |
0 |
-0,4 |
10 |
5000 |
300 |
0,2 |
0,2 |
0,1 |
-0,4 |
-0,1 |
11 |
4000 |
400 |
0,1 |
0,1 |
0,1 |
-0,7 |
0,6 |
12 |
7000 |
300 |
0,4 |
0,3 |
0,3 |
0,1 |
-0,6 |
13 |
4000 |
500 |
0,1 |
0,4 |
0,2 |
-0,4 |
-0,6 |
14 |
3000 |
600 |
0,2 |
0,2 |
0,2 |
-0,6 |
0 |
15 |
4000 |
300 |
0,3 |
0,5 |
0,1 |
0,5 |
0,5 |
16 |
3000 |
500 |
0,4 |
0,3 |
0,4 |
0,5 |
-0,4 |
17 |
6000 |
400 |
0,3 |
0,2 |
0,2 |
-0,5 |
0,5 |
18 |
5000 |
600 |
0,5 |
0,2 |
0,1 |
0,5 |
0,3 |
19 |
4000 |
400 |
0,3 |
0,3 |
0,2 |
-0,4 |
0 |
20 |
6000 |
300 |
0,4 |
0,2 |
0,3 |
-0,5 |
-0,4 |
6.6.3Порядок работы
1.На основе рис. 6.6.2, б и формулы (6.6.2) составить уравнения линий переключения с учетом времени запаздывания в устройстве управления.
2.По выражению (6.6.1) и рис. 6.6.2, б составить уравнения фазовых траекторий.
3.Решить уравнения динамики системы с учетом заданных начальных условий для каждой из зон, ограниченных линиями переключения. Начальные условия для каждой последующей зоны приравниваются конечным условиям предыдущего участка.
4.Построить линии переключения и фазовую траекторию в
фазовой плоскости в координатах x =v, y =vɺ для достаточно
большого промежутка времени, чтобы можно было определить
существование и параметры предельного цикла.

98
5. Задав начальные условия в другой области предельного
цикла3, построить ещё одну фазовую траекторию.
6.6.4Содержание отчета
Вотчете необходимо привести задание на выполнение лабораторной работы, исходные данные, уравнения линий переключения, фазовый портрет системы с изображенными линиями переключения, графики зависимости угла рассогласования и угловой скорости от времени, параметры предельного цикла, сделать выводы. При защите работы устно ответить на вопросы.
6.6.5Вопросы
1.Что такое фазовая плоскость?
2.Что характеризуют линии переключения?
3.Как составить уравнения фазовых траекторий?
4.Что такое предельные циклы и как их можно классифицировать?
5.Сколько в исследуемой системе зон с разным характером уравнений динамики?
6.Есть ли на фазовом портрете данной системы точки равновесия?
3 Внутри предельного цикла, если первая траектория начиналась вне предельного цикла, либо вне предельного цикла, если первая траектория начиналась внутри предельного цикла.
99
6.7 Лабораторная работа №6. Анализ нелинейной
системы с помощью частотного критерия В.М.
Попова
6.7.1 Цель работы Определить максимально возможный сектор расположения
нелинейной характеристики с помощью критерия Попова. 6.7.2 Основные соотношения
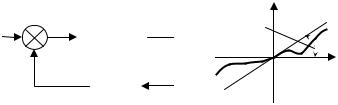
Структурная схема нелинейной САУ приведена на рис. 6.7.1, а.
|
|
|
|
|
y |
|
|
|
|
|
arctgK |
− |
|
W(s) |
|
x |
|
|
|||||
|
|
|
|
||
|
|
|
|
||
y |
|
|
|
x |
|
|
φ(x) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
б |
|
|
|
Рис. 6.7.1. Нелинейная система |
|||
По критерию Попова для абсолютной устойчивости системы (рис. 6.7.1, а) с нелинейностью, лежащей в секторе (0, K) (рис. 6.7.1, б), достаточно, чтобы видоизмененная частотная
передаточная |
функция |
устойчивой |
линейной |
части |
W (jω)= ReW(jω)+ jωImW(jω) |
располагалась правее |
прямой |
||
Попова, проведенной через точку −1 K на вещественной оси. Линейная часть задана одной из передаточных функций:
K на вещественной оси. Линейная часть задана одной из передаточных функций:
