
Информатика.-1
.pdf
150
Для построения линейной интерполяции служит встроенная функция linterp:
linterp(х,у,t) — функция, аппроксимирующая данные векторов х и у кусочно-линейной зависимостью:
х — вектор действительных данных аргумента;
у — вектор действительных данных значений того же размера;
t — значение аргумента, при котором вычисляется интерполирующая функция.
ВНИМАНИЕ! Элементы вектора х должны быть определены в порядке возрастания, т.е. Xl < X2 < X3 < ... < XN.
Пример линейной интерполяции. Листинг 1. Линейная интерполяция
Как видно из листинга, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:
Ввести векторы данных х и у (первые две строки листинга). Определить функцию linterp(х,у,t).
Вычислить значения этой функции в требуемых точках, например,
linterp(х,у,2.4)=3.52, или linterp(х,у,6)=5.9,
или постройте ее График, как показано на рис. 13.2.
ПРИМЕЧАНИЕ. Функция A(t) на графике имеет аргумент t, а не х. Это означает, что функция A(t) вычисляется не только при значениях аргумента (т.е. в семи точках), а при гораздо большем числе аргументов в интервале (0,6), что автоматически обеспечивает Mathcad. Просто в данном случае эти различия незаметны, т.к. при обычном построении графика функции А(х) от векторного аргумента х (рис. 7.17) Mathcad по умолчанию соединяет точки графика прямыми линиями (т.е. скрытым образом осуществляет их линейную интерполяцию).
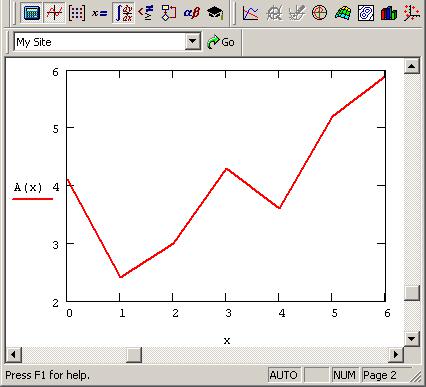
151
Рис. 7.17 — Обычное построение графика функции от векторной переменной х
7.10 Кубическая сплайн-интерполяция
В большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция кубическими сплайнами, т.е. отрезками кубических парабол:
interp(s,x,y,t) — функция, аппроксимирующая данные векторов х и у кубическими сплайнами:
s — вектор вторых производных, созданный одной из со-
путствующих функций cspline, pspline или lspline;
х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
у — вектор действительных данных значений того же размера;
t — значение аргумента, при котором вычисляется интерполирующая функция.
Сплайн-интерполяция в Mathcad реализована чуть сложнее
линейной. Перед применением функции interp необходимо

152
предварительно определить первый из ее аргументов — векторную переменную s. Делается это при помощи одной из трех встроенных функций тех же аргументов (х, у):
ispline(х,у) — вектор значений коэффициентов линейного сплайна;
pspiine(x,y) — вектор значений коэффициентов квадратичного сплайна;
cspline(х,у) — вектор значений коэффициентов кубического сплайна:
х,у — векторы данных.
Выбор конкретной функции сплайновых коэффициентов влияет на интерполяцию вблизи конечных точек интервала. Пример сплайн-интерполяции приведен в листинге 2.
Листинг 2. Кубическая сплайн-интерполяция
Смысл сплайн-интерполяции заключается в том, что в промежутках между точками осуществляется аппроксимация в виде зависимости A(t)=at3+bt2+ ct+d. Коэффициенты а, b, с, d рассчитываются независимо для каждого промежутка, исходя из значений у* в соседних точках. Этот процесс скрыт от пользователя, поскольку смысл задачи интерполяции состоит в выдаче значения A(t) в любой точке t (рис. 7.18).
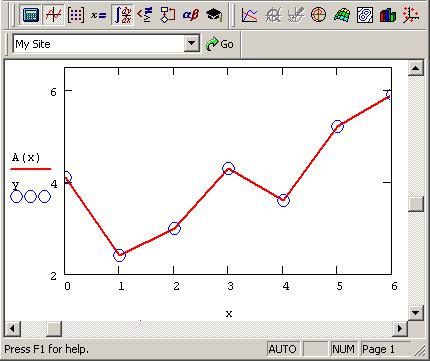
Чтобы подчеркнуть различия, соответствующие разным вспомогательным функциям cspline, pspline, ispline, покажем результат действия листинга 2 при замене функции cspline в предпоследней строке на линейную ispline (рис. 7.19). Как видно, выбор вспомогательных функций существенно влияет на поведение A(t) вблизи граничных точек рассматриваемого интервала (0,6) и особенно разительно меняет результат экстраполяции данных за его пределами.
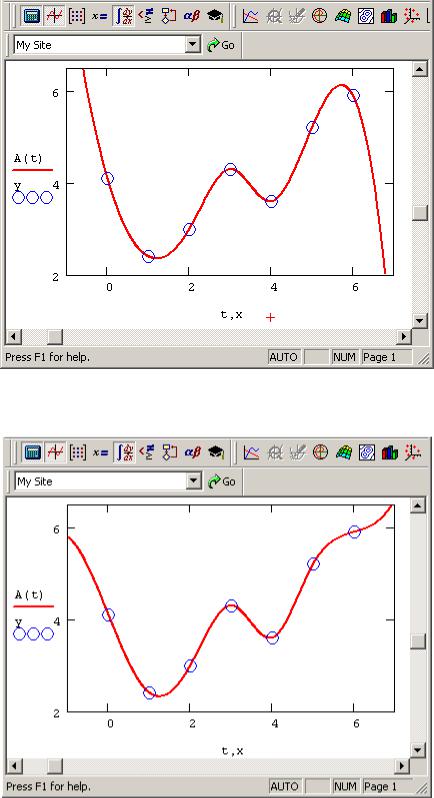
153
Рис. 7.18 —Сплайн-интерполяция (продолжение листинга 2)
Рис. 7.19 — Сплайн-интерполяция с выбором коэффициентов линейного сплайна lspline
154
В заключение остановимся на уже упоминавшейся в предыдущем разделе распространенной ошибке при построении графиков интерполирующей функции (см. рис. 7.17). Если на графике, например, являющемся продолжением листинга 2, задать построение функции А(x) вместо A(t), то будет получено просто соединение исходных точек ломаной (рис. 7.20). Так происходит потому, что в промежутках между точками вычисления интерполирующей функции не производятся.
Рис. 7.20 — Ошибочное построение графика сплайн-интерполяции
Полиномиальная сплайн-интерполяция
Более сложный тип интерполяции — так называемая интерполяция В-сплайнами. В отличие от обычной сплайнинтерполяции сшивка элементарных В-сплайнов производится не в точках хi а в других точках ui, координаты которых предлагается ввести пользователю. Сплайны могут быть полиномами 1, 2 или 3 степени (линейные, квадратичные или кубические). Применяется интерполяция В-сплайнами точно так же, как и обычная сплайн-интерполяция, различие состоит только в определении вспомогательной функции коэффициентов сплайна.

155
interp(s,x,y,t) — функция, аппроксимирующая данные векторов х и у с помощью В-сплайнов;
bspiine (x,y,u,n) — вектор значений коэффициентов В-сплайна;
s — вектор вторых производных, созданный функцией
bspline;
х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
у — вектор действительных данных значений того же размера;
t — значение аргумента, при котором вычисляется интерполирующая функция;
u — вектор значений аргумента, в которых производится сшивка В-сплайнов;
n — порядок полиномов онлайновой интерполяции (1, 2
или з).
ПРИМЕЧАНИЕ.
Размерность вектора и должна быть на 1, 2 или 3 меньше размерности векторов х и у. Первый элемент вектора и должен быть меньше или равен первому элементу вектора х, а последний элемент и — больше или равен последнему элементу х.
Интерполяция В-сплайнами иллюстрируется листингом 3 и
рис. 7.21.
Листинг 3. Интерполяция В-сплайнами
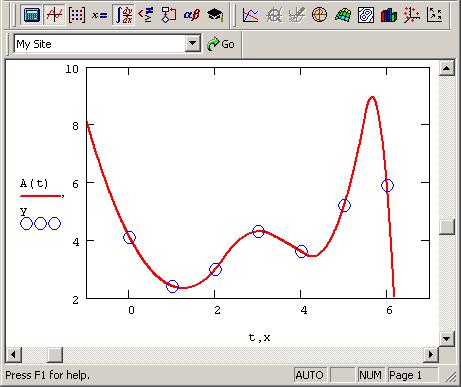
156
Рис. 7.21 — В-сплайн-интерполяция
7.11 Сплайн-экстраполяция
Все описанные выше функции интерполяции работают также и как функции экстраполяции данных. Для вычисления экстраполяции достаточно просто указать соответствующее значение аргумента, которое лежит за границами рассматриваемого интервала. С этой точки зрения разницы в применении в Mathcad между интерполяцией и экстраполяцией нет.
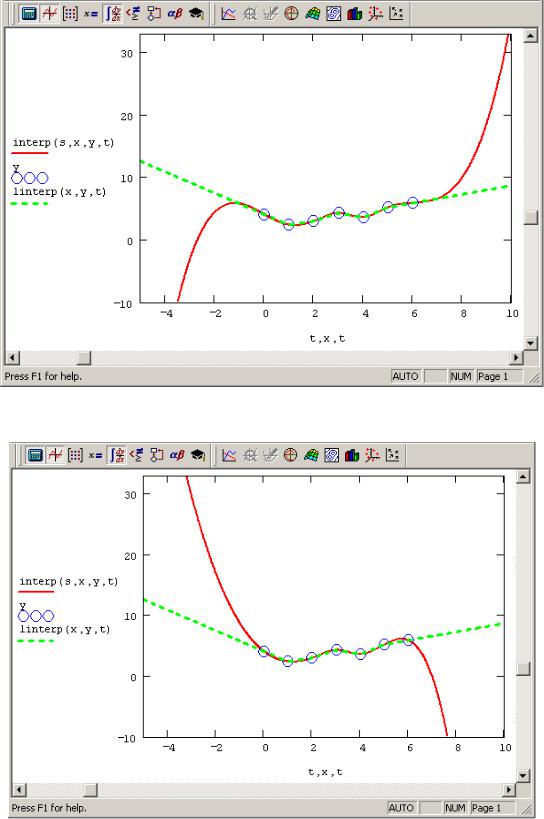
На практике при построении экстраполяции следует соблюдать известную осторожность, не забывая о том, что ее успех определяется значимостью ближайших к границе интервала точек. Чем дальше от них вы будете пытаться экстраполировать зависимость, заданную экспериментальными точками, тем сомнительнее будет результат. Сказанное иллюстрируется рис. 7.22 и 7.23, на которых изображена линейная (пунктир на обоих графиках) и сплайн — (сплошные кривые) экстраполяция. На рис. 7.22 используется линейная сплайн-экстраполяция при помощи функции ispline (см. рис. 7.19 в качестве примера интерполяции), а на рис. 7.23 — функции кубического сплайна cspline (что соответствует листингу 2 и рис. 7.18). Видно, что вдали от рассматриваемого
157
интервала результаты экстраполяции совершенно различны, что, конечно, объясняется тем, что она является ни чем иным как параболической зависимостью.
Рис. 7.22 — Линейная сплайн-экстраполяция
Рис. 7.23 — Квадратичная сплайн-экстраполяция
158
7.12 Многомерная интерполяция
Двумерная сплайн-интерполяция приводит к построению поверхности z (х,у), проходящей через массив точек, описывающий сетку на координатной плоскости (х,у). Поверхность создается участками двумерных кубических сплайнов, являющихся функциями (х,у) и имеющих непрерывные первые и вторые производные по обеим координатам.
Многомерная интерполяция строится с помощью тех же встроенных функций, что и одномерная (см. разд. ), но имеет в качестве аргументов не векторы, а соответствующие матрицы. Существует одно важное ограничение, связанное с возможностью интерполяции только квадратных NxN массивов данных:
interp(s,x,z,v) — скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами:
s — вектор вторых производных, созданный одной из со-
путствующих функций cspline, pspline или lspline;
х — матрица размерности Nх2, определяющая диагональ сетки значений аргумента (элементы обоих столбцов соответствуют меткам х и у и расположены в порядке возрастания);
z — матрица действительных данных размерности NxN;
v — вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция.
ПРИМЕЧАНИЕ.
Вспомогательные функции построения вторых производных имеют те же матричные аргументы, что и interp: lspline
(X, Y), pspline (X, Y), cspline (X, Y).
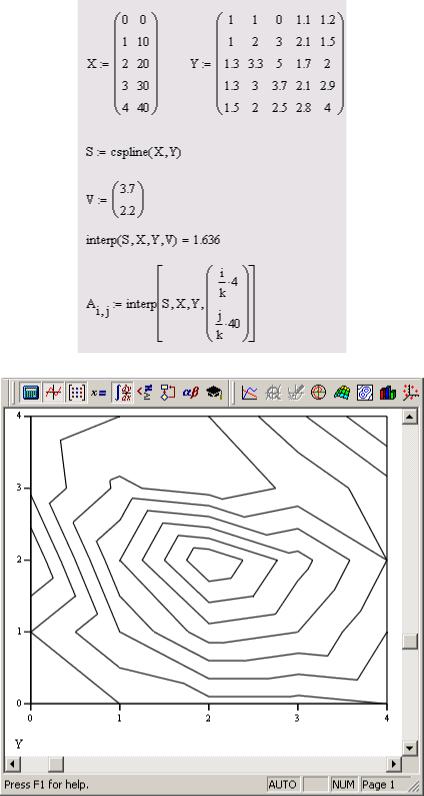
Пример исходных данных приведен на рис. 7.24 в виде графика линий уровня, программная реализация двумерной интерполяции показана в листинге 6, а ее результат — на рис. 7.25.
159
Двумерная интерполяция
Рис. 7.24 — Исходное двумерное поле данных
