Информатика.-1
.pdf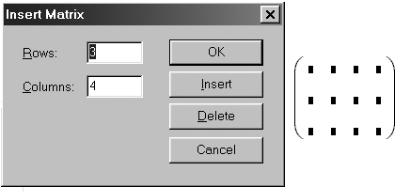
140
же рассмотрены некоторые функции, осуществляющие матричные операции, используемые при выполнении контрольных работ.
7.4.1Ввод и редактирование формата матриц с помощью шаблона
Интерфейс процессора MathCad позволяет вводить матрицы с помощью шаблона, задаваемого в диалоговом окне. Диалоговое окно вызывается командой главного меню Insert\ Matrix…, либо комбинацией клавиш-акселераторов Ctrl+M, либо воздействием («клик») на пиктограмму 
палитры матричных операций. Вид диалогового окна показан на рисунке 7.3. На этом же рисунке показан шаблон, возникающий в точке нахождения курсора после нажатия кнопки «ОК» в поле диалогового окна. В данном примере создан шаблон для занесения матрицы с тремя строками (Rows) и четырьмя столбцами (Columns). Заполнив знакоместа (выделены черными прямоугольниками) числовыми константами, либо формульными выражениями, получаем готовый объект — матрицу, с которым далее можно производить все допустимые действия.
Рис. 7.3 — Диалоговое окно и шаблон ввода матрицы
С помощью этого диалога можно редактировать формат уже созданных матриц, добавляя/удаляя строки и столбцы. Эти действия вызываются кнопками Insert и Delete. Для редактирования формата матрицы необходимо:
а) выделить некоторый элемент матрицы, подведя под него курсор;
141
б) вызвать окно диалога;
в) задать необходимые величины в полях Rows и Columns; г) нажать кнопку Insert или Delete.
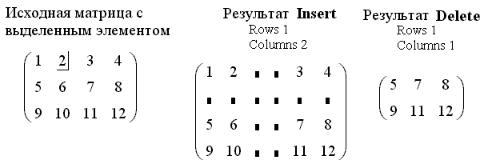
Пример редактирования существующих матриц с помощью диалога показан на рисунке 7.4.
Рис. 7.4 — Редактирование формата матриц с помощью окна диалога
Как видно из приведенного примера, вставка (Insert) заданного количества строк и столбцов происходит после строки и столбца с отмеченным элементом. Операция удаления (Delete) убирает заданное число строк и столбцов после строки и столбца с отмеченным элементом, включая строку и столбец с выделенным элементом. Если необходимо убрать\добавить только строки, то в поле Columns надо поставить 0, если необходимо убрать\добавить только столбцы, то надо задать Rows=0.
7.4.2 Функции компоновки и декомпозиции матриц
В составе библиотеки встроенных функций MathCad имеются функции, позволяющие производить, формировать матрицу из блоков-подматриц и выделять из заданной матрицы подматрицы нужного размера. Компоновку матрицы из блоков осуществляют функции augment, stack. Выделение подматрицы выполняется
функцией submatrix и оператором выделения столбца матрицы
M<>.
Функция augment объединяет матрицы-аргументы слева направо «столбец к столбцу», как показано на рисунке 7.5. Функция augment может вызываться с произвольным количеством аргументов, необходимым условием ее работы является равенство числа строк у всех матриц-аргументов.
142
Рис. 7.5 — Действие функции augment
Функция stack объединяет матрицы-аргументы сверху вниз «строка к строке», как показано на рисунке 7.6. Функция stack также может вызываться с произвольным количеством аргументов, а необходимым условием ее работы является равенство числа столбцов у всех матриц-аргументов.
Рис. 7.6 — Действие функции stack
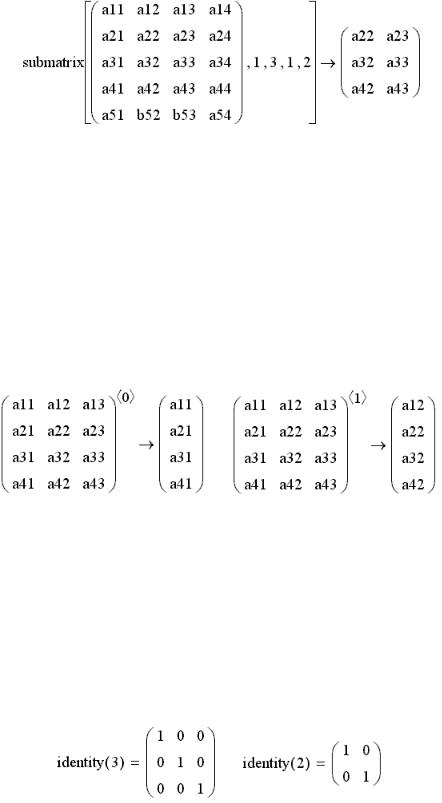
Функция выделения подматрицы submatrix имеет следующий синтаксис вызова:
submatrix (A, rb, re, cb, ce),
где A — исходная матрица, из которой извлекается фрагмент; rb — номер начальной строки в матрице A, включаемой в вы-
деляемую подматрицу;
re — номер конечной строки в матрице A, включаемой в выделяемую подматрицу;
cb — номер начального столбца в матрице A, включаемого в выделяемую подматрицу;
ce — номер конечного столбца в матрице A, включаемого в выделяемую подматрицу.
Функция submatrix (A, rb, re, cb, ce) работоспособна при вы-
полнении условий 0 re rb m–1 и 0 ce cb n–1, где m и n — соответственно число строк и столбцов в матрице A. (Напомним,
что нумерация строк и столбцов в MathCad по умолчанию начи-
нается с 0.) Пример действия функции показан на рисунке 7.7.
143
Рис. 7.7 — Действие функции submatrix
С помощью функции submatrix можно выделить любой прямоугольный фрагмент из матрицы. Для частного случая декомпозиции матрицы — выделения столбца с заданным номером — в наборе инструментов векторно-матричных операций MathCad имеется специальный оператор M<>, шаблон которого вызывается воздействием на элемент управления с пиктограммой. Пример применения оператора M<> приведен на рисунке 7.8.
Рис. 7.8 — Действие оператора выделения столбца M<>
7.4.3 Создание единичной и диагональной матриц
Для создания единичной матрицы заданного размера в MathCad можно использовать функцию identity(n). Эта функция возвращает квадратную единичную матрицу размера n n (рисунок 7.9), размещая ее в точке вызова функции.
Рис. 7.9 — Создание единичной матрицы функцией identity
Квадратная матрица размера n n, элементы которой отличны от нуля только на главной диагонали (диагональная матри-
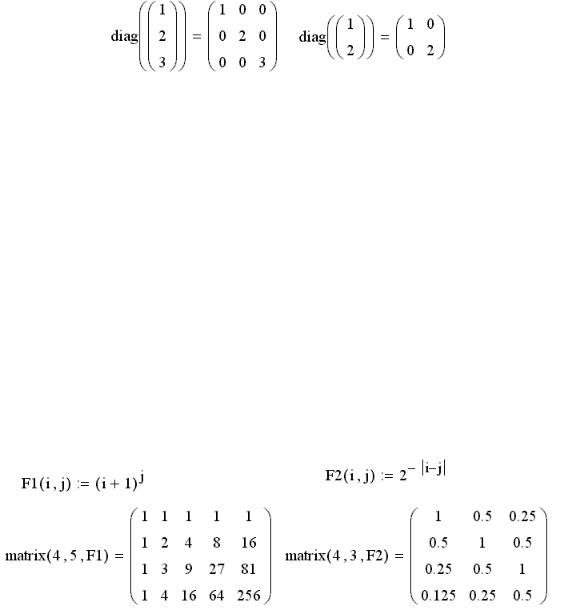
144
ца), может быть сформирована из вектора x размера n с помощью встроенной функции diag (x). Размер матрицы определяется автоматически по размеру вектора, а компоненты вектора встраиваются в диагональ в порядке своего расположения (рис. 7.10).
Рис. 7.10 — Результат работы функции diag
7.4.4 Формирование матрицы на основе заданной функции
В ряде случаев значения элемента матрицы aij можно связать со значениями его индексов некоторой функцией от двух целочисленных аргументов: aij = F(i,j). В этом случае матрицу произвольного размера можно сформировать при помощи встроенной функции matrix(m,n,F), где m и n — число строк и столбцов в создаваемой матрице, F — имя функции двух целочисленных аргументов, используемой для расчета элементов. Функция F(i,j) должна быть определена к моменту выполнения matrix.
Пример формирования матриц с различными функциями формирования значений элементов приведен на рисунке 7.11.
Рис. 7.11 — Формирование матриц функцией matrix
7.4.5 Поэлементное формирование матриц
Матрицу произвольного размера можно сформировать, задавая значение каждому элементу с помощью оператора назначения (рисунок 7.12). Перебор множества индексов может быть
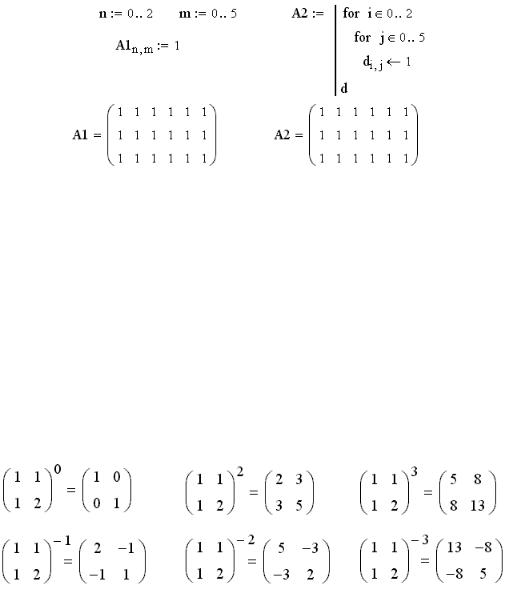
145
произведен с помощью ранжированных переменных (создание матрицы A1), либо с использованием операторов цикла в программном блоке (создание матрицы A2). Как видно из приведенного на рисунке 7.12 примера, результат абсолютно одинаков.
Рис. 7.12 — Поэлементное формирование матриц
7.4.6 Целочисленные степени квадратных матриц
В среде MathCad целочисленная степень матрицы (в том числе отрицательная) задается точно так же, как и степень обычных числовых переменных (рисунок 7.13). В том случае, когда матрица не имеет обратной, попытка вычислить ее какую-либо отрицательную степень блокируется с выдачей соответствующего сообщения. Нулевая и положительная степень квадратной матрицы вычисляются всегда.
Рис. 7.13 — Целочисленные степени квадратной матрицы
7.4.7 Функции определения размеров матриц
Возможны ситуации, когда для вычислительного процесса необходимы сведения о размерах матриц, которые становятся известны только после их формирования в ходе вычислений. Для получения такой информации используются функции определения количества строк и столбцов в матрицах rows и cols. На ри-
146
сунке 7.14 приведен пример довольно сложного формирования матрицы С из матриц А и В с использованием функций rows и cols для определения размеров промежуточных матриц.
Рис. 7.14 — Использование функций rows и cols
Применение функций rows и cols повышает универсальность выражений, использующих матричные операции, они становятся менее зависимыми от конкретных размеров исходных матриц. Так, например, в рассмотренном выше примере при произвольных размерах матриц A и B, допускающих их перемножение, вычислительные операторы выполнятся корректно.
7.5 Оператор | x |
Вызов шаблона оператора | x | может производиться из нескольких инструментальных панелей. Этот оператор многофункционален, результат его действия зависит от типа аргумента x. В программировании такое поведение функций называют полиморфизмом. Полиморфизм оператора | x | отражен в таблице 7.1.
Таблица 7.1
|
Тип аргумента |
|
|
Результат |
||
скаляр |
|
абсолютное значение числа |
||||
комплексное число a + ib |
модуль комплексного числа |
|||||
|
a2 b2 |
|
||||
|
|
|
||||
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||
вектор x2 |
|
|
|
|
||
модуль вектора: xk2 |
||||||
|
|
|
|
k 1 |
||
|
|
|
|
|
||
|
|
|
|
|
||
xn |
|
|
|
|
|
|
квадратная матрица |
определитель |
|||||
147
Расчет определителя квадратной матрицы в MathCad производится оператором |A|. Попытка применить этот оператор к неквадратной матрице с количеством столбцов более одного вызывает ошибку.
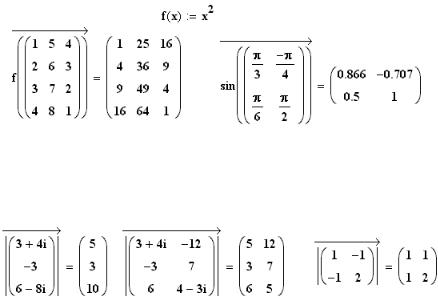
7.6 Оператор векторизации функций
В наборе инструментов матричных операций имеется оператор векторизации функций. Пусть f(x) определена как функция скалярного аргумента и задана M — матрица произвольных размеров с элементами Mij. Операция векторизации функции f(x) вызывает появление матрицы с элементами f(Mij), т.е. происходит поэлементное функциональное преобразование матрицы — аргумента в матрицу — результат того же размера. Например:
Векторизация меняет смысл оператора | x |, рассмотренного выше:
Как видно из приведенных примеров, векторизованный оператор | x | выполняет замену элементов матрицы их абсолютными величинами, причем для комплексных чисел берется модуль. Матрица-аргумент может быть произвольного размера.
Операции векторизации нет в математике, это специфическая функция MathCad. Заметим, что векторизация функций не
имеет ничего общего с матричными функциями от квадратных матриц, рассмотренными в п. 2.3.
148
7.7 Интерполяция и регрессия
Этот раздел посвящен методам обработки выборочных данных — интерполяции, экстраполяции и регрессии. Будем считать, что основным объектом исследования будет выборка экспериментальных данных, которые, представляются в виде массива, состоящего из пар чисел (xi,yi). Возникает задача аппроксимации дискретной зависимости y(xi) непрерывной функцией f(x). Функция f(х), в зависимости от специфики задачи, может отвечать различным требованиям:
f(x) должна проходить через точки (xi,yi), т.е. f(xi)=yi, i=1..n. В этом случае говорят об интерполяции данных функцией f(х) во внутренних точках между xi или экстраполяции за пределами интервала, содержащего все хi;
f(х) должна некоторым образом (например, в виде определенной аналитической зависимости) приближать y(xi), не обязательно проходя через точки (xi,yi). Такова постановка задачи регрессии.
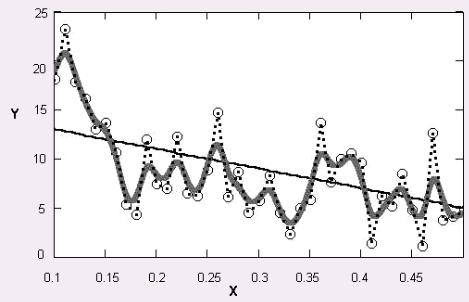
Различные виды построения аппроксимирующей зависимо-
сти f(х) иллюстрирует рис. 7.15.
Рис. 7.15 — Разные задачи аппроксимации данных
На нем исходные данные обозначены кружками, интерполяция отрезками прямых линий — пунктиром, линейная регрессия — наклонной прямой линией, а фильтрация — жирной гладкой кри-
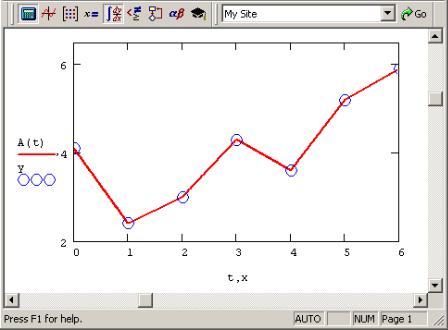
149
вой. Эти зависимости приведены в качестве примера и отражают лишь малую часть возможностей Mathcad по обработке данных. Вообще говоря, в Mathcad имеется целый арсенал встроенных функций, позволяющий осуществлять самую различную регрессию, интерполяцию и экстраполяцию.
7.8 Интерполяция
Для построения интерполяции-экстраполяции в Mathcad имеется несколько встроенных функций, позволяющих «соединить» точки выборки данных (xi,yi) кривой разной степени гладкости. По определению интерполяция означает построение функции А(Х), аппроксимирующей зависимость у(х) в промежуточных точках (между xi). Поэтому интерполяцию еще по-другому называют аппроксимацией. В точках xi значения интерполяционной функции должны совпадать с исходными данными, т.е.
A(xi)=y (xi).
7.9 Линейная интерполяция
Самый простой вид интерполяции — линейная, которая представляет искомую зависимость А(Х) в виде ломаной линии. Интерполирующая функция А(х) состоит из отрезков прямых, соединяющих точки (рис. 7.16).
Рис. 7.16 — Линейная интерполяция