
Радиотехнические цепи и сигналы. Часть 2 Дискретная обработка сигналов и цифровая фильтрация
.pdf
161
2.Определение импульсной характеристики (по таблице 8.3).
3.Выбор подходящей функции окна (по таблице 8.6).
4.Расчёт сглаженной импульсной характеристики.
Таблица 8.6 – Аналитическое представление оконных функций во временной и частотной областях
Название |
Дискретная временная функция |
Частотная характеристика |
||||||||||||||||||||||||
окна |
|
|
|
w n |
|
|
|
|
|
|
W k |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Прямоуг. |
|
w n 1, 0 n N 1 |
|
|
sin k |
e |
j k N 1 N |
|||||||||||||||||||
|
|
WD k |
sin k N |
|
|
|
|
|
|
|
||||||||||||||||
(окно |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
wD n 0, |
ïðè äð. n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Дирихле) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
WD k |
D k N |
|
|
|
|
|
|
||||||||
Косинус- |
w |
Õàí |
n 1 cos2 n N 1 |
WХан k 0,5D k N |
||||||||||||||||||||||
|
0,5cos 2n N 1 , |
|
|
|||||||||||||||||||||||
0,5 |
|
|
||||||||||||||||||||||||
квадрат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(окно |
0 n |
N 1 |
|
|
|
|
|
|
0,25D k 1 N |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ханна) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
wÕàí |
n 0, ïðè äð. n |
|
|
0,25D k 1 N |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Приподн. |
|
|
|
|
|
2 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
wÕýì n 0,54 0,46cos |
|
|
|
, |
WХэм k 0,54D k N |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
косинус |
|
|
|
|
|
N |
1 |
|
|
|
1 |
N |
|
|||||||||||||
(окно |
0 n N 1 |
|
|
|
|
|
|
0,23D k |
|
|||||||||||||||||
|
|
|
|
|
|
0,23D k 1 |
N |
|
|
|
|
|
||||||||||||||
Хэмминга) |
wÕýì n 0, ïðè äð. n |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
WБл k 0,42D k N |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
2 n |
|
|
0,25D |
|
|
|
k |
N |
|
|
|
|
|||||||||
|
wÁë n |
|
|
|
|
|
N |
|
|
|
|
1 |
|
|||||||||||||
|
0,42 0,5cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Обобщ. |
|
|
|
|
N 1 |
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|||||
косинус |
|
|
|
4 n |
|
|
|
0,25D |
|
|
|
k |
N |
|
|
|
|
|||||||||
(окно |
0,08cos |
|
, |
|
|
|
|
N |
|
|
|
|
1 |
|
||||||||||||
N 1 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2N |
|
|||||||||||
Блэкмана) |
0 n N 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
wÁë n |
0, |
ïðè |
äð. n |
|
|
0,04D |
|
k |
N |
|
|
|
|
||||||||||||
|
|
|
|
|
N |
|
|
|
|
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2N |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
0,04D |
|
k |
N |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
162 |
|
|
|
|
|
|
|
|
|
|
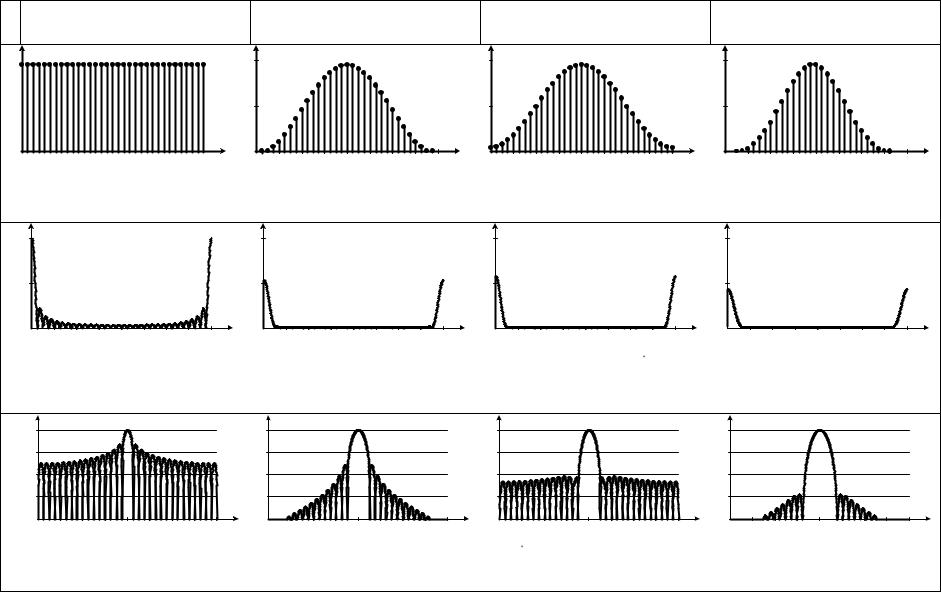
Таблица 8.7 – Графическое представление оконных функций во временной и частотных областях |
|
|
|
||||||||||||||||
|
Прямоугольное окно |
|
Квадрат косинуса |
|
Приподнятый косинус |
|
Обобщенный косинус |
||||||||||||
|
(Окно Дирихле) |
|
|
(Окно Ханна) |
|
|
(Окно Хемминга) |
|
(Окно Блэкмана) |
|
|||||||||
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
0 |
8 |
16 |
24 |
32 n |
0 |
8 |
16 |
24 |
32 n |
0 |
8 |
16 |
24 |
32 n |
0 |
8 |
16 |
24 |
32 n |
|
|
|
|
|
|
Дискретные временные функции окон w(n) |
|
|
|
|
|
|
|||||||
32 |
|
|
|
|
32 |
|
|
|
|
32 |
|
|
|
|
32 |
|
|
|
|
16 |
|
|
|
|
16 |
|
|
|
|
16 |
|
|
|
|
16 |
|
|
|
|
0 |
|
π |
|
2π |
0 |
|
π |
|
2π |
0 |
|
π |
|
2π |
0 |
|
π |
|
2π |
|
|
|
|
|
Амплитудно-частотные характеристики окон W (k) |
|
|
|
|
|
|||||||||
0 |
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
- |
|
|
|
|
- |
|
|
|
|
- |
|
|
|
|
- |
|
|
|
|
20 |
|
|
|
|
20 |
|
|
|
|
20 |
|
|
|
|
20 |
|
|
|
|
-60 |
|
|
|
|
-60 |
|
|
|
|
-60 |
|
|
|
|
-60 |
|
|
|
|
-π |
|
0 |
|
π |
-π |
|
0 |
|
π |
-π |
|
0 |
|
π |
-π |
|
0 |
|
π |
|
|
|
Амплитудно-частотные характеристики окон W (k) в логарифмическом масштабе |
|
|
|
|||||||||||||
163
Таблица 8.8 – Значения основных параметров оконных функций
Наименование |
|
Название окна |
|
|
параметра |
Дирихле |
Ханна |
Хэмминга |
Блэкмана |
Ширина |
|
|
|
|
главного |
1/N |
2/N |
2/N |
3/N |
лепестка |
|
|
|
|
Ширина |
|
|
|
|
перехода |
0,9/N |
3,1/N |
3,3/N |
5,5/N |
ˆ ˆç ˆï |
|
|
|
|
Неравномерность |
|
|
|
|
АЧХ в полосе |
0,7416 |
0,0546 |
0,0194 |
0,0017 |
пропуск. Aп , дБ |
|
|
|
|
Главный |
|
|
|
|
лепесток отн-но |
13 |
31 |
41 |
57 |
боковых, дБ |
|
|
|
|
Неравномерность |
|
|
|
|
АЧХ в полосе |
21 |
44 |
53 |
75 |
загражд. Aз , дБ |
|
|
|
|
Коэффициент |
|
|
|
|
пульсаций, % |
22,34 |
2,62 |
1,47 |
0,08 |
N=11 |
|
|
|
|
Коэффициент |
|
|
|
|
пульсаций, % |
21,89 |
2,67 |
0,93 |
0,12 |
N=21 |
|
|
|
|
Коэффициент |
|
2,67 |
0,82 |
0,12 |
пульсаций, % |
21,8 |
|
|
|
N=31 |
|
|
|
|
8.6Пример синтеза КИХ-фильтров методом оконных функций
Разработать цифровой КИХФНЧ с параметрами:
частота дискретизации – 128 кГц;
граничная частота полосы пропускания – 14,72 кГц;
ширина полосы перехода – 12,8 кГц;
затухание АЧХ в пределах полосы подавления – 44 дБ.
1. Выбор оконной функции по таблице 8.7. Требованиям к затуханию в полосе подавления удовлетворяют функции Ханна, Хэмминга и Блэкмана. Для простоты выберем окно Ханна.

164
wХан n 0,5 0,5cos 2n  N , 0 n N 1 wХан n 0, при др. n
N , 0 n N 1 wХан n 0, при др. n
2.Определение нормированной ширины перехода
ˆ f  fä 12,8
fä 12,8 128 0,1
128 0,1
3.Вычисление порядка фильтра из соотношения (см. табл. 8.7)
N 3,1 ˆ 3,1
ˆ 3,1 0,1 31
0,1 31
4.Расчет нормированной частоты пропускания
ˆï |
ï |
ä fï |
fä 14,72 128 0,115 |
5. Определение идеальной импульсной характеристики из таблицы 8.3
|
sin 2 n ˆ |
ï |
|
|
sin 0,23 n |
, при n 0 |
|
g(n) 2 ˆ |
|
|
|
0,23 |
|
||
|
|
|
|||||
|
ï |
2 n ˆï |
|
|
|
0,23 n |
|
|
|
|
|
|
|
||
g(n) 0,23, при n 0
6. Определение смещенной импульсной характеристики
|
N 1 |
|
sin 0, 23 |
|
|
|
|
|
|
|
|
|
|
|||
g n |
|
|
0, 2 |
|
n |
|
|
N 1 |
2 |
|
при 0 |
n N 1 |
||||
2 |
|
0, 23 |
|
n |
|
N 1 2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
g n N 1  2 0, 23
2 0, 23
Здесь N=31.
7. Умножение смещенной импульсной характеристики на оконную функцию
gñãë n g n- N-1  2 wÕàí n
2 wÕàí n
8. Определение системной функции фильтра, сглаженного с помощью окна Ханна
K z |
N 1 |
gcãë n z n |
|
||
|
n 0 |
|
9. Определение комплексной передаточной функции цифрового КИХфильтра, сглаженного с помощью окна Ханна
ˆ |
N 1 |
|
ˆ |
|
n |
|
|
|
j2 |
|
|||
K |
gcãë n e |
|
|
|
||
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
В таблице 8.9 приведены результаты расчетов коэффициентов КИХфильтров различного назначения, сглаженных с помощью оконных функций. В таблице 8.10 представлены импульсные и частотные характеристики рассчитанных фильтров после применения оконных функций.
165
Таблица 8.9 – Коэффициенты КИХ-фильтров, (ФНЧ, ФВЧ, ПФ, РФ) сглаженных с помощью оконных функций
|
ФНЧ |
ФВЧ |
ПФ |
РФ |
g0 g30 |
0 |
0 |
0 |
0 |
g1 g29 |
-1,5835 10-4 |
1,5835 10-4 |
2,3626 10-4 |
- 2,3626 10-4 |
g2 g28 |
0,3325 10-4 |
- 0,3325 10-4 |
1,9147 10-3 |
1,9147 10-3 |
g3 g27 |
1,734 10-3 |
1,734 10-3 |
1,4889 10-3 |
1,4889 10-3 |
g4 g26 |
4,766 10-3 |
4,766 10-3 |
3,3079 10-3 |
3,3079 10-3 |
g5 g25 |
6,438 10-3 |
6,438 10-3 |
0 |
0 |
g6 g24 |
2,6655 10-3 |
2,6655 10-3 |
8,4433 10-3 |
8,4433 10-3 |
g7 g23 |
8,5824 10-3 |
8,5824 10-3 |
-0,0105 |
0,0105 |
g8 g22 |
-0,0236 |
0,0236 |
-0,0454 |
0,0454 |
g9 g21 |
-0,0323 |
0,0323 |
-0,033 |
0,033 |
g10 g20 |
-0,0217 |
0,0217 |
0 |
0 |
g11 g19 |
0,0165 |
-0,0165 |
-0,0632 |
0,0632 |
g12 g18 |
0,0794 |
-0,0794 |
-0,1736 |
0,1736 |
g13 g17 |
0,1511 |
-0,1511 |
-0,0895 |
0,0895 |
g14 g16 |
0,2082 |
-0,2082 |
0,2175 |
0,2175 |
g15 |
0,23 |
0,77 |
0,4 |
0,6 |
|
|
|
|
|
166 |
|
|
|
|
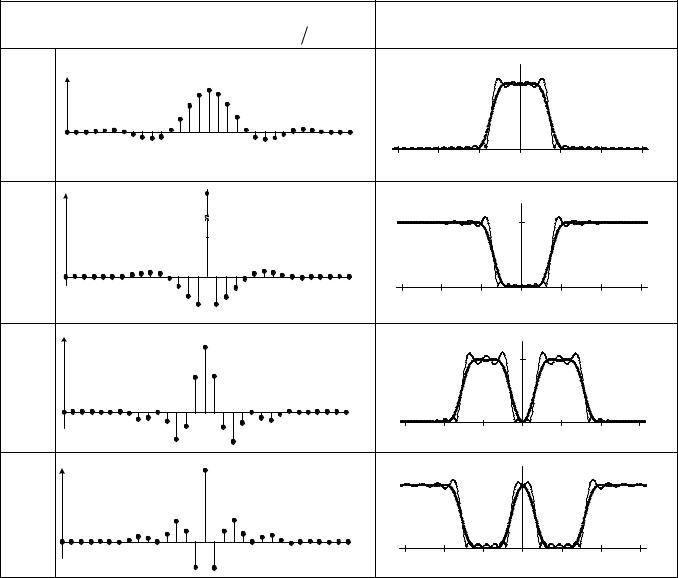
Таблица 8.10 –Сглаженные импульсные и частотные характеристики |
|
||||||||
цифровых частотно-избирательных КИХ-фильтров (ФНЧ, ФВЧ, ПФ, РФ) |
|
||||||||
Тип фильтра и сглаженные импульсные |
Частотные характеристики до и |
||||||||
характеристики gñãë(n N 1 2) |
|
|
после оконной функции |
|
|||||
|
|
|
|
|
|
|
|
^ |
|
g(n) |
|
|
0,23 |
|
|
|
|K(ω)| |
|
|
|
|
|
|
|
1 |
|
|||
ФНЧ |
|
|
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
-0,5 |
|
^ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0,5ω |
||
g(n) |
|
|
0,77 |
|
|
|
^ |
|
|
|
|
|
0,2 |
|
|
|
|
|K(ω)| 1 |
|
ФВЧ |
|
|
|
|
|
|
|
|
|
0 |
5 |
1 |
15 |
20 |
25 |
30 |
-0,5 |
0,5 |
^ |
|
|||||||||
0 |
ω |
||||||||
|
|
|
|
|
|
|
|
|
|
g(n) |
|
|
0,4 |
|
|
|
|
^ |
|
|
|
|
|
|
|
|K(ω)| |
|
||
|
|
|
|
|
|
|
|
1 |
|
ПФ |
|
|
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
-0,5 |
0,5 |
^ |
|
|
|
|
|
|
|
ω |
||
g(n) |
|
|
0,6 |
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|K(ω)| 1 |
|
РФ |
|
|
|
|
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
-0,5 |
0,5 |
^ |
|
|
|
|
|
|
|
ω |
||

167
9 ПРИЛОЖЕНИЯ
9.1 Приложение 1
9.1.1 Описание пакета программ для исследования частотных и временных характеристик цифровых фильтров, синтезированных методом Билинейного z-преобразования
Известная системная функция цифрового фильтра позволяет
определить его частотную характеристику следующим образом: |
|
Ê ˆ K å j2ˆ . |
(9.1) |
Приведенное выражение может быть использовано для расчета АЧХ цифрового фильтра, однако данный путь не является самым простым в рассматриваемом случае. При заданной АЧХ аналогового фильтра-прототипа
ˆ |
Ê ˆ может быть приближенно вычислена, |
Ê АЧХ цифрового фильтра |
если учесть трансформацию частотной оси. Необходимое соотношение имеет вид
ˆ |
|
|
|
|
2 |
|
Ò |
|
|
|
|
|
|
|
|
||||||
|
|
|
||||||||
|
|
Ê |
|
|
tg |
|
. |
(9.2) |
||
Ê |
|
|
|
|
||||||
|
|
|
|
|
Ò |
|
2 |
|
|
|
|
|
|
|
|||||||
Таким образом, если аналоговыми фильтрами-прототипами служат фильтры Чебышева и Баттерворта N-го порядка, то для АЧХ цифровых фильтров могут быть записаны следующие формулы:
Ê Á ˆ |
|
|
|
|
1 |
|
|
, |
|
Ê× ˆ |
|
|
|
|
|
1 |
|
|
|
|
, (9.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
tg ˆ |
2N |
|
|
|
|
|
|
|
|
|
2 |
||||||
|
|
|
1 2 |
|
|
|
|
|
|
|
1 2 |
T |
|
tg ˆ |
|
|||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
||||||
|
|
|
|
|
tg ˆï |
|
|
|
|
|
|
|
|
tg ˆï |
||||||||
Приведенные соотношения (9.3) рекомендуется использовать для расчета АЧХ цифровых фильтров. Следует отметить, что в силу периодичности рассматриваемых функций расчет нужно проводить лишь дляˆ 0;0,5 . Кроме того, при построении АЧХ чебышевского типа полезно
предварительно выяснить расположение нулей и максимумов функций ÒN ˆ
при ˆ 1 [8], что позволяет грамотно выбирать шаг по частоте и не пройти мимо характерных точек АЧХ в полосе пропускания цифрового фильтра.
Для визуализации результатов расчетов в среде Windows на языке программирования C++ с использованием библиотеки Qt v.4.2.0 разработан пакет прикладных программ, позволяющий анализировать частотные и временные характеристики цифровых фильтров (ЦФ) разного назначения.
168
Полная структурная схема ЦФ представлена как последовательное включение биквадратных звеньев. Для определения временных характеристик использованы методы расчета отклика ЦФ на воздействие цифровых дельта-функции и единичного скачка.
Алгоритм работы i-го биквадратного звена ЦФ описывается уравнением
вида:
yi(n) xi(n) Ai xi(n1) Bi xi(n 2) Ci yi(n1) Di yi(n 2) (9.4)
где i – номер звена;
Ai, Bi, Ci и Di – коэффициенты взвешенного суммирования.
При помощи выражения (9.4) рассчитываются импульсные характеристики всех звеньев фильтра. С помощью свертки импульсных характеристик звеньев gi(n) друг с другом и умножения полученного
результата на нормировочный множитель K 0 , получается импульсная
характеристика ЦФ, представленного каскадным включением биквадратных звеньев.
gn K0 g1(n) g2(n) g3(n) ... gq(n) |
(9.5) |
где q – количество звеньев.
Переходная характеристика ЦФ рассчитана свёрткой импульсной
характеристики с цифровой функцией единичного скачка ( n 1,1,1...). |
|
hn gn n |
(9.6) |
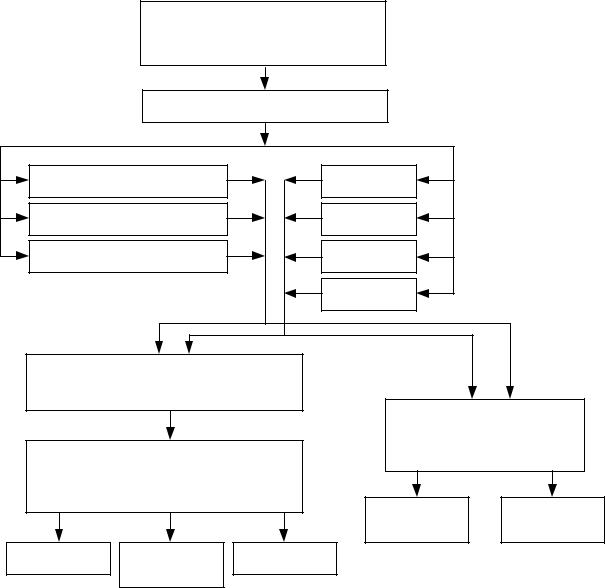
На рисунке (9.1) показана блок-схема алгоритма расчета временных и частотных характеристик ЦФ, примененного в программе.
Отклик определен свёрткой импульсной характеристики со входной последовательностью.
|
|
yn gn xn |
|
|
(9.7) |
|||
Для определения частотных характеристик ЦФ использованы |
||||||||
системные функции K(z) , |
представленные в виде произведения системных |
|||||||
функций каждого биквадратного звена K |
i |
(z) , при z e j T : |
|
|||||
|
|
|
|
|
|
|
|
|
K (z) K 0 K1 (z) K 2 (z) K3 (z) ... K q (z) |
(9.8) |
|||||||
K (e j T ) K |
0 |
K (e j T ) K |
2 |
(e j T ) ... K |
q |
(e j T ) |
(9.9) |
|
|
1 |
|
|
|
|
|||
|
|
169 |
|
|
Задание граничных частот, |
|
|
|
порядка фильтра и значений |
|
|
|
неравномерности АЧХ ЦФ |
|
|
|
Выбор типа фильтра |
|
|
Фильтр Баттерворта |
ФНЧ |
|
|
Фильтр Чебышева I |
ФВЧ |
|
|
Фильтр Чебышева II |
ПФ |
|
|
|
|
РФ |
|
Расчет коэффициентов |
|
||
биквадратных звеньев |
|
||
|
|
Расчет комплексной |
|
|
|
системной функции |
|
Формирование алгоритмов |
ЦФ |
||
|
|||
работы звеньев ЦФ |
|
||
|
|
Расчет |
Расчет |
|
|
АЧХ |
ФЧХ |
Расчет g(n) |
Расчет |
Расчет h(n) |
|
|
|
||
|
отклика |
|
|
Рисунок 9.1 – Блок-схема алгоритма расчета временных и частотных |
|||
|
|
характеристик ЦФ |
|
Амплитудно-частотная характеристика (АЧХ) рассчитана как произведение модулей комплексных функций биквадратных звеньев. Фазочастотная характеристика (ФЧХ) определена как сумма аргументов комплексных функций биквадратных звеньев.
