Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Радиотехнические цепи и сигналы. Часть 1 Теория сигналов и линейные цепи

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

24.88 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2717 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

160

− K

(p)

−

2Re[Re s ],

h(t )= L

= L

(p − p1 )(p − p1)

Re s

= lim

(p − p

)e pt

(p − p

)(p − p )

p= p

−α + jωсв

e(−α + jωсв )t =

ω p

e−α t e j(ωсвt −Ψ+π 2),

2 jωсв

2ωсв

h(t )= −

ω p

e−α t sin(ωсвt − Ψ) σ (t ),

где Ψ = arctgωсв

2ωсв

Проверимвыпредолнсоотношенийниельных:

lim K (p)= 0,

lim h(t )= 0,

p→0

t →∞

lim h(t ) =

ω p

sin Ψ =

lim K(p)=1,

t→0

ωсв

p→∞

ω p

св

ω p

св

sin arctg

= 1.

ωсв

α ωсв

1 + (ωсв α)2

Проверправильностьм

связимеждупереходнойиимпульсной

характеристиками

g(t )= hʹ(t )= − ω p {[e−α tσ (t )] sin(ωсвt − Ψ)}ʹ,

ωсв

g(t )= − ω p {[−α e−α t σ (t )+ δ (t ) e−α t ] sin(ωсвt − Ψ)+

ωсв

+[ωсв cos(ωсвt − Ψ)][e−α tσ (t )]}=

= −	ω p	{− δ (t )sin Ψ + e−α t [ωсв cos(ωсвt − Ψ)−α sin(ωсвt − Ψ)]}=
= −
ωсв
= δ (t )+			ω 2p	e−α t sin(ωсвt − 2Ψ) σ (t ).
= δ (t )+				e−α t sin(ωсвt − 2Ψ) σ (t ).
			2ωсв
Нарисункеизоб6.временныехарактеристики11ажены
последовательконоготура						2p
				lim g(t )= −	ω	2p	sin 2Ψ = −2α .
				lim g(t )= −			sin 2Ψ = −2α .

t →+0 ωсв

161

g(t )

h(t )

− 2α	t	0	t
	а)		б)
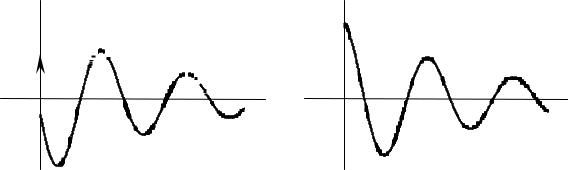
Рисунок6.11	– Импульсная)(ипереходнаяб()хар		актеристики

последовательногоконтура

Втаблице6представлены.5 аналитическвыражпер даточныхиея функцийвременныххарактеристикпростейшихизобразительныхцепей.

Втаблице6показ.6модуличастотныхкоэффициентовпередачи, такжеимпульсные переходныехарактэтихжцепей.ристики

6.5 Выводы
1. Влинцесигнайнпиодвергаютсяйлинейнымпрео			бразованиям.
МгновезначесигвходенаиаловыевыходеяЛЭЦсвязанымеждусобой
линейнымдиффеуравнениеменциальняннымиспосткоэффиц ент			ами.
2. Частотныйкоэффициентпередачилинпредставляетйнойпи
собойдробно -рационфункциючальнуюстмобытьжеттыопределенкак
отношениекомплекснамплитудыгармсигналаойвыходеического
комплекснойамплитудегармонич		ескогосигналавходеЛЭЦ.
3Спектральная. плотностьвыходсигявляетсяпралаогоизведением
часткоэффтногопередачиспектральнойциентаплотсигналаости
выходелине	йнойцепи.
4Реак. линцеиянавозйнойпидельйставие			-функцииили(
единичногоскачка)называетсявремен		нойхарактеристикойЛЭЦ	−
импульснили(перех). одной
5Частотный. коэффпередачиимпульснаяциентхарактеристика
цеписвязаныпаройпреобразованийФурье.
6Прим. преобразовнениеЛапласкдифференциальномуния
уравнениюэлектрическогоравновесияпо		звопрляпередаточнуюдели ь
функциюЛЭЦвоператорнойформезаписи.
7Переход. коперационномуисчислсущупрощаетниюственно

расчетывременныххарактеристик.Особенноэтопроявляетсяприанализе колебательныхцепей.

Таблица6

.5 – Передаточныефункциивременныехарактеристикипростейшихизбирательныхцепей

Схемаконтура

Передаточная

Импульсная

Переходная

функция

K (p), Z (p)

характеристика

2 pα

g(t )= −

2αω p

[e−α t ×

h(t ) =

2α

e−α t sinωсвt σ (t )

C L

K (p)=

ωсв

2 pα + ω p

× sin(ωсвt − Ψ)] σ (t )

g(t )= δ (t )+

ω 2p

[e−α t ×

h(t )= −

ω p

e−α t ×

C R

K (p) =

ωсв

+ 2 pα + ω p

× sin(ωсвt − 2Ψ)] σ (t )

× sin(ωсвt − Ψ)] σ (t )

h(t )

ω p

−α t

K (p) =

ω p

g(t )

ω p

−α t

sinωсвt σ (t )

= 1 −

ωсв

2 + 2 pα +ω 2p

ωсв

× sin(ωсвt + Ψ)] σ (t )

2α ω

( )

ω p

(p + 2α ) C

[e−α t ×

h t

= R

рез

−

g(t )= Rрез

Q ωсв

Z (p)=

ωсв

+ 2 pα + ω p

× sin(ωсвt + Ψ)] σ (t )

× e

−α t

sin(ωсвt + 2Ψ)] σ (t )

Условныеобозначениясвязьм нимижду

ω p

ωсв

ω p

ωсв

, Q =

, R рез =

ω p =

, α =

, Ψ = arctg

, ω p

= ωсв

+α

−1.

2α

ω pC

ωсв

4Q2 −1

162

								2
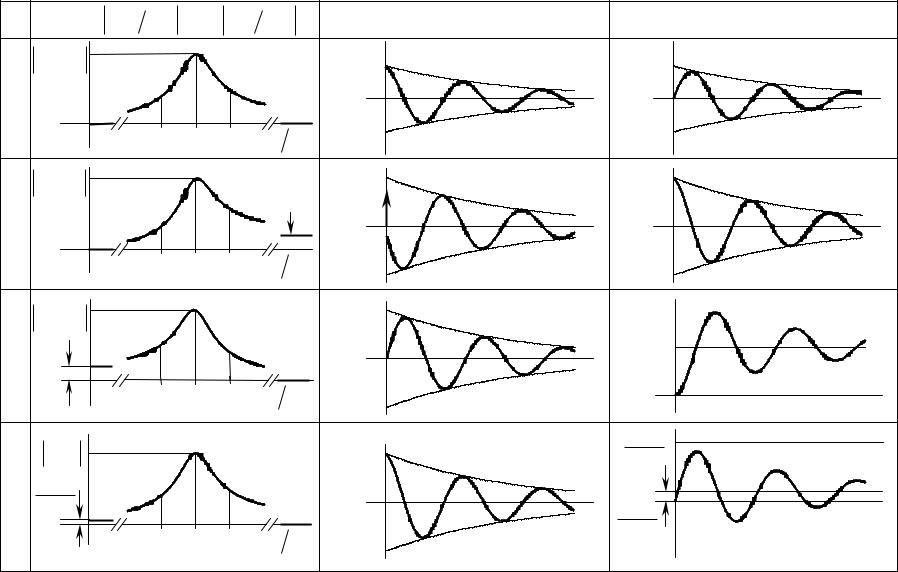
	Таблица6		.6	–	Графическоепредставлениечастотныхвременныххарактеристикпростейших
избирательныхцепей			(	)
			(	)	или			( )			h(t )
		K	ω ω p			Z (ω ω p )		g t			h(t )
							2α	1,46α	1,06α	0,2
1	KR (n)		0,406				2α	1,46α	1,06α	0,2
			0,406			0,48
	0								t		t
	0		0,8		1	1,2	ω ω p
2							ω			1
2	KL (n) Q					0,58Q
		0,33Q					1
							1
	0						− 2α		t		t
	0		0,8		1	1,2	ω ω p				163
3							ω p
3	KC (n) Q 0,51Q					0,4Q
	1					0,4Q				1
	0								t
	0		0,8		1	1,2	ω ω p				t
			0,8		1	1,2	ω ω p				t
4	Z (n)						2αRрез			1
	Z (n)	Rрез								ω pC
	R рез									ω pC
	R рез									R рез
	Q2								t	R рез	t
			0,8		1	1,2	ω ω p			Q2

ω = 0 .Амплитудыгармконическихлебаний

	164
7ПРОХОЖДЕНИЕСИГНАЛ	ОВЧЕРЕЗЛИНЦЕЙНЫЕ	ПИ

7Анализ.1прохожденпериодическихсигналовя черезлинцметодпи(йныекомплексныхамплитуд)

Периодическийсигнал,проходячерезЛЭЦ,нетеряетсвоей периодическойприроды,поэтомусигналы входеивыходелинц йнойпи можнопредставитьбескосуммойнеперечнойсигналов,одических сдвинутыхдруготносительнодруганапериод:

∞

s(t ) = ∑sT (t + nT )

n=−∞	∞	(7.1)

sвых (t ) = ∑sвыхT (t + nT )

n=−∞

Применяядляописасигтрниалгяофнвозаписрмуметрическую

рядаФурье,п

олучим:

∞

s(t ) =

∑An cos( nω1t + ϕn )

n=1

∞

cos(nω t + ϕ

)

s (t ) =

∑

nвых

вых

2 вых

n=−∞

Используемдлярасчетапаравыходнпеетриовсигналадического

методкомплексныхампл,сч,чтоитмплекснаяудпередаточная

функция K (ω ) известна:

jϕ(nω1)

K (nω1)

(7.2)

(7.3)

Постояннаяоставлвыходепрямопропорциональнающаязначению коэффициентапередачипри умножаютсязначенимодулякомплекспередаточнойфунакции

частотах ω = nω1 .Начальныефазыгармконическихлебансумм руютсяй созначениямифазочастотнойхарактерисЛЭЦначастотахики

a				a
	o		=	o	K (0 ),
	2			2
		вых

Anвых = An K (nω1 ) ,

ϕnвых = ϕn + ϕ(nω1 ).

ω = nω1 .

(7.4)

165

ПериодическийсигналвыходеЛЭЦописываетсярядом

	ao	∞
		K (0) + ∑ An		cos[nω1t + ϕn + ϕ(nω1 )].
sвых (t) =	2		K (nω1 )		(7.5)
		n=1

Частотныйметоданализа,использованныйданнслучае,позволяетм получитьясноепредсттом,какобразомвлениеизменяетсяспектр ходногопери дич ескогоси гнала.

На,припрохождениимерпериодичсигналачерФНЧэнезского гиявыходсигбудетнсалаосредотговнизкобластиоч,.е.астотнойена происходитувеличениеамплитудгармоникобластинижнихчастототн ситве.льрхноих

Пример7.1

Произведемср авнитеанаширинылспектраизьныйпериодической следовательностипрямоугоимпульсовнавходевыходеьныхинтегр

ющей RC - цепочки,изобнарисункеаженной7.1 . Сигналвходеопишемсуммойгармк ническихлебанийобщегов

∞

2Eτ

sin nω1 τ

cos(nω t −π

)

∞

sin nπ

cos(nω t

s(t) =

∑

где T

2τn.=1

nω1

n=1

Найдемкомпередаточнуюлексфу кцию 2

RC -

2цепиеечасто

ныехарактеристикиАЧХФЧХ.

1 jωC

K (ω ) =

R +

1 + jωRC

jωC

Полагая ω = nω1,

ω1RC = 0.5,получим:

K (nω ) =

1 + jnω1RC

1 + j0.5n

K (nω1)

1 + (0.5n)2

ϕ(nω1) = −arctg0.5n.

Сигналвыходе

RC - цеопределимкаксуммугармонических

лебаний,амплитудыначальныефазкотоопрепоыхформуламделяется

(7.4):

ы-

р-

о-

о- иру-

ида:

−π 2),

т-

о-

(t ) =

∞

sin nπ 2

cos[nω t − π

− arctg0.5n].

∑

вых

n =1 1 + (0.5n)

СпектральныедиаграммысигналоввходевыходеЛЭЦизобразим нарисунке7.1.

166

s(t)

sвых(t)

A7 A9

а)

A11

A13

ω1

0 ω1

3ω1

7ω1

11ω1

15ω1

K(ω)

ϕ(ω)

б)

Anвых

0.9 A1

в)

0.55A

0.37A5

ω1

3ω1

7ω1

11ω1

15ω1

nω1

Рисунок7.1 − ПрохождениепериодичсигналачерФНЧ: зского а)спектрпрямоугоимпульсовнавходеФНЧ;ьных б) амплитудно-частотнфазочастотнаяи х рактеристикиФНЧ; в)спектрсигналавыходеФНЧ

Втаблицепредставим7.1численныезн чениямплитудгармоник
входногоивыходсиг. налогов
Таблица7.1		−СпектрыамплнавходеивыходетудЛЭЦ
n	1		3	5	7	9	11	13
An	1		0.333	0.200	0.143	0.111	0.09	0.077
K(nω1)	0.9		0.555	0.374	0.275	0.217	0.179	0.155
Anвых	0.9		0.185	0.074	0.039	0.024	0.016	0.012

			167
Сравниваяскоростьзатуханиясп				екпотаблицеров7оцениваяш.1			и-
ринуспектпороговомукритериюа,видим,чтовыходлосиганалаого
приблизительнов меньшеазаполосывходного.
Рассмотренныйметодпозвоисскачественныеляетедиватьценить
количествизмен,происхоенияные			дящиевспектресигнала.
Чтобыизучитьизмеформынеобходиниявыполнсуммировть							а-
ниебесконелигармоникчсопределенныминогоестваамплитудами
начальнымиф	азами.
7Опера.2 методрасчетаткликарннавыходелинейной
цепрроизво			льномнепериодическомвоздействии
Воснэтогометодавележитпроведенная						в пар6а.графелгебраизация2
диффеуравненияэлектрическогоенцильногоп мощьюпрямвесияго
преобразоЛаплас.Возквраащаясьнияивычобозсигналовачениямым
входе s(t ) инавыходе		sвых (t ),перепишуравн(6виде.14)нием
		S вых ( p) = S ( p) K ( p) .
Еслипередаточнаяфункцияцепи					K ( p) известна,торешенразбиев		а-
етсянаэтапа3:					S( p)
1) расчетизображениявходногосигнала					S( p)
			S ( p) = L [s(t )];
2) расчетизображевыходсигналаияого		Sвых( p)			S( p)	Sвых( p)
				=		;
3) расчеторигиналакликвыходеЛЭЦ						K( p)
3) расчеторигиналакликвыходеЛЭЦ			(t ) = L−[S ( p) K ( p)].
		s	(t ) = L−[S ( p) K ( p)].
		вых
Еслинавходелинейнойсистемыдействуетпроизвольный							непериоди-
ческийсигнал,меняющийматематическоеописаннескраз, излько							об-
ражениебудетпредсобойтавлятьуммуизображеэлементарныхс ий							остав-
ляющих.
Приисследовапрохождсигчерезнлиаловинсиейныесялтемы							е-
дуетпомнпрсуперпозинципеть			циолипринципенезависимостиде				й-
ствия.Согласноэтомупринц,входнсигналслпуформыжнойможно
представлятьсуммойэлементарныхвоздейсиопределятьнакавийлик							ж-
доеэлементарноевоздействиеотдельно.Суммированиеэлементарныхоткл							и-
ковдастых	однойсигнал.
Следоват,входнойсигналце есообрразбивьнонаэлементазтьо							р-
ныесоставляющие.Умножениеизображеэлемсоставляющейниярной
входногосигнала	Si ( p)напередаточнуюфунклинцеиюйнойпи						K ( p)

позволяетопредеизображеэлитьеменсоставляющейвыходногоиерной сигнала Siвых ( p).

168

ОбратноепреобразовЛапласпозвперейоизображениялитниеи

элементавыходорисигкнала. гоиналу

c+ j∞

siвых (t ) =

S i ( p) K ( p) e pt dp.

∫

2πj

Пример7.2

c− j∞

Навходцепи,состоящ

ейизпоследоватсоединсопротивленныхльно

е-

ния R иемкости

C ,подаетнеперсигналятреугольнойодическийформы,

изобнарисункеаже7.2 .ный

Определиманалитическоевыр пряжнимкостипривыния

пол-

ненииусловий(

ατ = 0.25,1 ,4)где,

α =

s(t)

sвых(t)

Рисунок7.2

Аналитописа,изобгческоеналаиенарисуаже6пре.5,нкеного

д-

ставляетсобойследующвыраж: ение

0 ≤ t ≤ 2

s(t ) =

−τ ) ,

≤ t ≤τ

ИзображениевходнсигнпЛ гонайдемпласу,приППЛ. еняя

pτ

−

S( p) = ∫

2E t e− p t dt − ∫

2E (t −τ ) e− p t dt = 2E

(1− 2e

2 + e− pτ ).

Анализизображенпоказывает,чтовходнойсиможногналяпредст

а-

витьвзвешен

нойсуммойтреходинаковыхсигнал,сдвинутыхдруготнос

и-

тельнодругавовремени.

s(t)

s1(t)

s3(t)= s1(t-τ)

Здесь:

s1(t )

tσ (t );

s2 (t ) = −

(t − τ

)σ(t − τ

);

s2(t)= -2s1(t-τ)

s3 (t ) =

(t −τ )σ(t −τ ) .

Рисунок7.3

– Разложетреугольногосигналаие

ющие

элеменсоставлярные

169

Выпоинтервальноеолописаниеимвходнсигнагомощьюэла	е-
ментарныхсоставляющих

S1 (t),

0 ≤ t < τ 2,

S(t) =

S (t) − 2S

(t −τ 2),

τ 2 ≤ t < τ,

S (t) − 2S

(t −τ 2)+ S

(t −τ ),

t ≥ τ.

Опрердефункдаточнуюлимлинце.июйнойпи

K ( p) =

1 pC

,где

α = 1

R + 1 pC

pRC + 1

p +α

Sвых1( p):

Определимизобр

ажениеэлементарвыходсигналаого

Sвых1( p) = S1( p) K ( p),

Sвых1( p) = 2E

Определимэлементарныйотклик.

p +α

c+ j ∞

2Eα

sвых1(t ) =

∫

e p t dt = ∑

Res j .

2πj c− j ∞

p2 ( p +α )

j =1

Подынтегральвыражсо особыержитвениеточки, азываемыеое

полюсами:

p2 ( p +α) = 0,

p1 = 0,

p2 = −α,

k1 = 2,

k2 = 1.

p2 = −α -

Первыйполюс

p1 =0 имееткра ность

k1 = 2,второйполюс

простой,.е.кратностьегоравна1Опре. вычетыделимвухточках:

Res

= lim

2 E α

( p − p )2 e p t =

(2 −1)!

( p +α)

2Eα

p t

( p +α) − e

p t

e p t

p = 0 =

(αt −

1) , t ≥

dp p +α

ατ

( p +α)

Res

lim

2Eα

( p − p

) e p t = 2 E e−α t ,t ≥ 0.

=−α

( p +α)

α τ

Суммирвычеты,полуячим

= 2 E [α t − (1− e−α t )], t ≥ 0 .

(t ) = Res

+ Res

вых1

α τ

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2717 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]