Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Радиотехнические цепи и сигналы. Часть 1 Теория сигналов и линейные цепи

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

24.88 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2716 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

150

Запишемередаточныефункциитр сучетхпейобозначенийм

RC =τ , R L = 2α, ω p = 1

K (p) =

,при

τ → ∞ K (p) ≈ 1

pτ

pτ +1

(p) =

pτ

,при

τ → 0 K2 (p) ≈ pτ ,

pτ +1

(p) =

2 pα

,где

α <<ω p.

p2 + 2 pα + ω р2

Нарисунке6пок.7 асположениезано

нулейиполюсовна

p-плоскости

длятрпередаточныхфункций

jω

po1

α = 0

−α

α =ω р

− jω

a) p = −α

б) p = −α

в) p = −α ±

α 2 − ω

1,2

po1 = 0

Рисунок6.7

− Полюсы (×)инули(0)трпередаточныхфункций

K1( p), K2 ( p), K3( p)

Коэффициенты αn и

βm передаточнойфункции

K ( p) вещественны,

поэтомунулиполюса

либовещественны,лиобкомплексноразуют

сопряженпары.Дляслучаев,когданулиыеполюсырасполагаютсяна

действительной, уществуетграфоаналитическийприем

–

методБоде,

позволяющийизобразитьАЧХФЧХлинцеспомощьюйнойпиграфиков

функции 20 log10

K(ω)

Од,внастоящееаковреэтимметодомпрактическинепользуются,

таккакприменкомпьютернойтехникиниепозволяетрассчипос роитьать

АЧХиФЧХлюбойцепи.Втаблицах6.приведены63.4частотные

временныехарактеристикипро

стейшихэлектрическихцепей.

151

6.Расчет4.временных2 характеристиклинц йныхпей

Приопределенииимпульснойхарактеристнеобхпроверить, д кимо удовллипередаточнаятворяфункциятребованиям,предъявляемымк изображениямпоЛапласу(5.12) .

lim K (p) = 0.

p→∞

Этоуслмоневжетыполнятьсяиенапр( ,дляфильтровмерверхних

частот),.е.

lim K(p) = Mo pn−m

m > n

= n

p→∞

Mo,

Вэтомслучаеизпередаточнойфункцииследувыделчасуюять

K (p) = M o +

A(p) − M o B(p)

B(p)

Применяяобратноепреобра

зованиеЛакперласадвумым

передаточнымфункциям,получим

e− tτ σ (t ),

g1 (t ) = L− [K1 (p)] = L−

p + 1

g2 (t ) = L− [K 2 (p)] = L−

= L− 1 −

p + 1

p +

	1				e− tτ σ (t ).
= L− [1]− L−	τ		= δ (t )− 1

p +		1		τ
		τ

Третьяпередаточнаяфункцияимеетдвакомплексно						-сопряженных олюса
	p2 + 2 pα + ω p2 = 0,
	= −α ±
p	= −α ±	α 2 − ω	2	= −α ± jω	св	,
1,2			p		св

где ωсв = 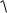ω р2 −α 2 ,т.е ω p2 = ωсв2 + α2.

152

Таблица6.3

– Частотныеивременныехарактеристикипростейших

ЛЭЦматематические( модели)

Электрическая

Частотныехарактеристики

Временныехарактеристики

Цепь

ЛЭЦ

Передаточнаяфункция

K (p),

Переходная h(t) и

Наименование

АЧХиФЧХ

импульсная g (t )

(ω )

характеристики

K(ω)

K (p)=

p +

g(t )=

−

σ (t )

Интегрирующа

яцепь

K (ω )

− t

h(t )=

(t )

) + ω 2

1 − e

ϕ(ω )= −arctgωτ

K (p)=

p + 1

g(t )= δ (t )−

e− tτ

σ (t )

Дифференциру

K (ω)

(1τ )2

+ ω2

щаяцепь

h(t )= e

− t

τ σ (t )

ϕ(ω)=

− arctg

K (p)=

2 pα

2αω р

Избирательная

2 + 2 pα + ω р 2

g(t )= −

e−αtσ (t )

ωсв

цепь

(послед ователь

K (ω )

sin(ωсвt −Ψ )

ный

− ω р

2α

колебательный

2ωα

−αt

h(t ) =

sinωсвt

(t )

контур)

ωсв

ϕ(ω)= −arctg

(ω2

−ω

2 )

ωсв =

ω р 2 − α 2

2ωα

				153
Таблица6.4	− ЧастотныеивременныехарактеристикипростейшихЛЭЦ
(графичмод) елиские
Электрическаяцепь			Частотные					Временные
			характеристикиЛЭЦ				характеристики ЛЭЦ
Схема			АЧХиФЧХ				Переходнаяиимпульсная
								характеристики
								g(t)
RC =τ		1	K(ω)				1	g(t)
RC =τ		1					1
							τ
R		C					0	h(t)		t
		C								t
		0	ϕ(ω)			ω	1
		0				ω

		0				ω
						ω	0
			−π / 2				0			t
			−π / 2							t
								g(t)
RC =τ		1	K(ω)
RC =τ

C							0			t
C									1
		R							1
		0				ω		h(t)	τ
		π ϕ(ω)				ω		h(t)
		π ϕ(ω)
		2
		0				ω	0			t
							0			t
								h(t)
α =	R		K(ω)			1
α =	2L						0			t
	1						0
ω р =	1
ω р =	LC
	LC
L			−ω р	0	ω р ω			g(t)
L			ϕ(ω)
		R	ϕ(ω)
		R					0			t
C				0		ω	0

154

Импульснаяхарактеристикадлятретьперфункциидаточнойравна

суммедвухкомп

лексно-сопряжвычилиудвоеннойтовнныхреальнойчасти

одизногоихприсложении( двухкомплексно

-сопряженныхполюсов

мнимыечастисокращаются).

(t) = L−

2 pα

= Re s + Re s

= 2Re[Re s

(p − p1)(p − p2 )

Re s

= lim

2 pα

(p − p

) e pt

2 p1α

e p1t

(p − p )(p − p

)

p − p

p= p1

p1, 2 =−α ± jωсв

2α(− α + jωсв )

e(−α + jωсв ) t =

α α + ωсв

ωсвt +

−Ψ

e−α t e

2 jωсв

ωсв

где Ψ = arctg

ωсв

3(t )

= −

2ω pα

e−α t sin(ω

св

t − Ψ)

σ (t).

ωсв

Используя(

6.рассчитаем17),переходныехарактеристикитрех

линейныхцепей.

Переходхарактеристикаинтегаяцепиавнаирующей

(t) = L−

K1 (p)

= L−

1 τ

= L−

−

= (1− e−α t ) σ (t)

p( p +1 τ)

p p

+ α

Дифференцирующаяцеопьисывпереходнойрактеристикойется

вида

− K2 (p)

−

−t τ

h2 (t) = L

= e

σ (t).

p +1 τ

Переходнаяхарактеристика

избирательнойцепределится

следующимобразом:

− K3 (p)

−

2α

h3 (t ) = L

= L

= 2 Re[Re s p1 ] =

(p − p

)(p − p

)

2α

− 1

2α

p t

= 2 Re p − p

L p − p

= 2 Re p − p

−(α + jωсв ) t

2α

−α t

cos(ωсвt −

) σ (t ).

= 2 Re

jωсв

ωсв

155

6.Расчет4.частотных3 ивременныххарактеристикпараллельного

избирательногоконтура

Схемапаризбирательноголлелькоегочастотныетура

характеристикиизображ

енрисункеыа6.8.

АЧХ

ФЧХ

i(t)

C uк (t)

ω ω p

− π 2

а)

б)

Рисунок6.8

– Схема)(параллельногоконтураичастотныеб()

характеристикиАЧХ( иФЧХ)

Навходедействуетток

i(t ),навыходеимеемнапряжение

u(t ),поэтому

системнаяфункцияцепиимеетразмерн

остьопротивления

[Ом].Определим

входноесопротивлениец операторнойпиформзаписи.

1 pC (pL + R)

p + 2α

где α = R

Z ( p) = pL + R + 1 pC = C (p2 + 2 pα + ω 2p ),

− коэффициентзатуханияконтура,

− резонансная

частота.

Z (p) ккомплефунчастотыкциисной

(ω),заменив

p на

Перейдемот

jω ираздечислительзнаменательвобщиймножитель

j2ωα .

1 − j

ω p

Z (ω )= R рез

ω p

1 + jQ

−

ω p

R рез =

где

Q =

2α

−

добротностьконтура,

ω pC

−

резонансное

сопротивление.

Частотныехарактеристики,иммодульнноАЧХ()аргументФЧХ()

комплекснвходнсопропределим, готивлениягопоформулам

156

Z (n)

= R рез

1 +1

(Qn)2

1 + [(n − 1

) Q]2

arg Z(n)= −arctg 1Qn − arctg[(n − 1n) Q],

где n = ω .

ω p

Нарисунке6изображе.8 частотхарактныпараллельногористики

контурадлядобротности

Q =10.

g (t ) ипереходной

h(t ) характеристик

Длярасчетаимпульсной

резонансковоспользуемсянтурагоизображениямиЛапласу

Z (p)

L[g(t )]= Z (p)

L[h(t )]=

ПрименимобратноепреобразоЛаплас(5ите.11)овычетахремуние

(5Найдем.48)полюсы.функции

Z ( p),приравнива язнаменателькнулю.

p2 + 2 pα + ω

= (p − p

)(p − p

)= 0,

p1,2 = −α ± jωсв ,

где ωсв = ω2p −α 2 − часвтособств(бодныхта)колебанийконтуранных.

Полюсы p1 и p2 представляютсобойкомплексно		−сопряженнуюпару,
поэтомувычетыбудутком	плексно−сопряженныфункция,		ми
суммированиекоторыхприводитудвоениюреальнойчасокращениюти
мнимой.
Re s1 + Re s2 = 2 Re[Re s1].
Будемрассчиттолькоодинвылюбойчева(изкомплексноть			-
сопряженнойпары).
Представим Z (p) ввиде

Z (p)=

p + 2α

C(p − p )(p − p

)

Re s

= lim

p + 2α

(p − p )e pt

C(p − p )(p − p

)

p = p

p1 + 2α

e p1t =

α + jωсв

e(−α + jωсв )t =

)

C(p − p

C 2 jω

св

2 + ω

j ωсвt +Ψ −

ω p

св

e−α t e

2Cωсв

	π
j ωсвt +Ψ −
	2
		,

где Ψ = arctgωсв α .

157

Импульснуюхарактеристопредел,взявудвоеннуюреальнуюимку часть Re s1.

g(t )=

ω p

e−α t sin(ωсвt + Ψ)= 2α

ω p

R рез e−α t sin(ωсвt + Ψ) σ (t ),

Cωсв

ωсв

ω p

св

4Q2 −1

ωсв

ω2p −α 2

4Q2 −1

g(t )

= 2α Rрез

e−α t sin(ωсвt + Ψ) σ (t ).

4Q2

−1

Провпереходноймрасчетхарактериспараллельногоконтикиура

h(t )= L−

p + 2α

Анализзнаменатель,ви,чторуядим,кромедвухкомплексно

C p(p

− p1 )(p − p2 )

−

сопряженныхполюсов

p1 и p2 ,появилсятрет

ий p3 = 0.

Re s

= lim

p + 2α

(p − p

)e pt

C p(p − p

)(p − p

)

p = p

p1 + 2α

p t

α + jωсв

−α t

jω

св

(p − p

)

C (−α + jω

)

2 jω

св

j ωсвt + 2Ψ +

+ ωсв

e−α t e

2Cωсв

α 2 + ωсв2

2 Re[Re s

]

= −

e−α t sin(ω

св

t + 2Ψ ),

Cωсв

p + 2α

2α

Re s

lim

(p − 0)e pt =

p= p3 =0 C p(p2 + 2 pα + ω

2 )

Cω2

Объединяявычеты,получим

2α

e−α t

h(t )=

−

sin(ωсвt + 2Ψ) σ (t ).

св

Замечание.

Cω p

Обращаем

вним,чтонаразмниемпульснойрностяхи

переходнойхарактеротразистиклась

мерностьсистемнойфункции

контурасопротивления( )

Ом

[g(t )]=

[h(t )]= Ом

сек

Нарисунке6изоб.9 временныеаженыхарактеристикипараллельного избирательногоконтура

158

2αRрез

g(t )

h(t )

ω pC

R рез

а)

б)

Рисунок6.9

– Импульсная)(ипереходнаяб()характеристикипаралл

ельного

избирательногоконтура

Взаключенпроверимвы олнсоотношенийд ниельных:

lim Z (p)= 0,

lim h(t )= 0,

t →0

p→∞

Rрез

lim h(t )=

рез

lim Z (p) =

2α

= R.

Cω

t →∞

p→0

6.Расчет4.частотных4 ивременныххарактеристикпослед

овательного

избирательногоконтура

Схемапоследоватизбирательногоконтурачастотные

характеристикиизображенынарисунке6.10.

АЧХ

K(n) Q

ФЧХ

π 2

ω ω p

а)

б)

Рисунок6.10

– Схема)(последоваконтураичастотныеб()ельного

характеристики

K (p)=

pL + R + 1 pC

= p2 + 2 pα + ω 2p ,

159

( jω )2

ω p

K (ω )=

2 jωα + ω

− ω 2

ω p

1 + jQ

−

ω p

Q n

K(n)

ϕ(n)= π 2 − arctg[(n − 1 n) Q].

Здесь α = R

1 + [(n − 1 n) Q]2

, Q = ω p

, ω

= 1

n =

ω p

2α

Передрасчетомимпульснойхарактеробращвнинтостикимание,чтоем

lim K(p)=1.

Раздечисзнаменательливтель,выделимиз

p→∞

K (p) целуючасть

p2 ± (2 pα + ω 2p )

K (p)=

2 pα + ω

−

p2 + 2 pα + ω 2p

У,чтемо

p2 + 2 pα +ω2p = (p − p1)(p − p2 ),а

p1 и p2 − комплексно−

сопряженныеполюса

p1,2 = −α ± jωсв

g(t )= L− 1 −

2 pα + ω p

= δ (t )− L−

2 pα + ω p

= δ (t )− 2Re[Re s ],

(p − p

)(p − p

)

(p − p )(p − p

)

2 pα +ω 2

2α (−α + jω

св

)+ω 2

Re s

= lim

(p − p

)e pt

e(−α + jωсв )t

(p − p )(p − p

)

2 jω

p= p1

св

Подставляя ω2p −α2 =ωсв2 ,получим

(−α + jω

Re s

− 2 jωсв α − ω p

св

= −

2 jωсв

= −

(α − jωсв )

e(−α + jω

св )t

= −

ω p

e−α t e j(ωсв t −2Ψ−

2),

2 jωсв

2ωсв

где Ψ = arctg

ωсв

ω 2p

g(t )= δ (t )+

e−α t sin(ωсвt − 2Ψ) σ (t ).

2ωсв

Расчетпереходнойхарактеристикиневызатрудненийывает

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2716 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]