Радиотехнические цепи и сигналы. Часть 1 Теория сигналов и линейные цепи

S2 (ω ) =

1

=

− j

2ωα

;

(α + jω )2

(α2 + ω2 )2

(α2 + ω2 )2

lim Re S2 (ω ) = lim

= −

1

;

α →0

α →0 (α2 + ω2 )2

ω2

lim Im S2 (ω ) = − lim

2αω

=

0 , ω ≠ 0

α →0

α →0 (α2 + ω2 )2

− π δ ʹ(ω ), ω = 0.

Изпрошлогопримера

знаем,что

lim

α

= πδ (ω ).

2 + ω2

α →0 α

Продифференцировавпо

ω правуюилевуючасти,получим

2ωα

lim −

= πδ ʹ(ω ) .

2 + ω2 )2

α →0 (α

Такимобразом,спектральнаяплотностьсигнала

tσ (t ) равна

Ф+[tσ (t )]= π δ ʹ(ω ) −

1

.

ω2

Дальнейшиеперехо

дывы,полнимрименяясвойствапреобразований

Лапласа.Втаблицах5.5стр4.5132(

−135)представленыразнообразные

сигналыихиз

ображенияпоЛапФурьеоласу.

5Практ.6 приложениекпятойческоеглав

5.Математическое6.1 описаниепростодносйших

торонсигналових

ирасчетизображенийпоЛапласу

Нарисунке5показаны.3сигналыоригиналы( ),представляющиесобой

произвлинарастающейеденйнофункцииединскачныхков

Выполнимматематическоеопишестсигналанпомэл щьюв

е-

ментарныхсоставляющиху

становимсвязьмеждувсемисигналами:

s (t) =

E

t σ (t) ;

1

to

s

2

(t) =

E

(t − t

0

) σ (t) =

E

tσ (t) − Eσ (t) = s (t) − Eσ (t);

to

to

1

s (t) =

E

(t − t

o

) σ (t − t

o

) = s (t − t

o

) ;

3

to

1

122

S5 ( p)

+ E

t

+ E

(t − to ) σ (t

=

E

1

−

E

1

e

− pt

o ;

= L

σ (t)

− L

− to )

to

to

to p2

to p2

S6 ( p)

+ E

t

+ E

t σ

=

E 1

−

E 1

e

− pt

o

−

E

e

− pt

o .

= L

σ (t)

− L

(t − to )

to p2

to p2

p

to

to

Прирасчетезображенийшессигналовтолькоодинразвыполнялось

интегрированиепочастям.Востальныхслучаябылииспольсвязиованы

междусигналами,которыеприм асчетеинялисьизображений.

5.Расчет6.изображений2 поЛапласуодносзатухающихоронних

гармоничколебанийских

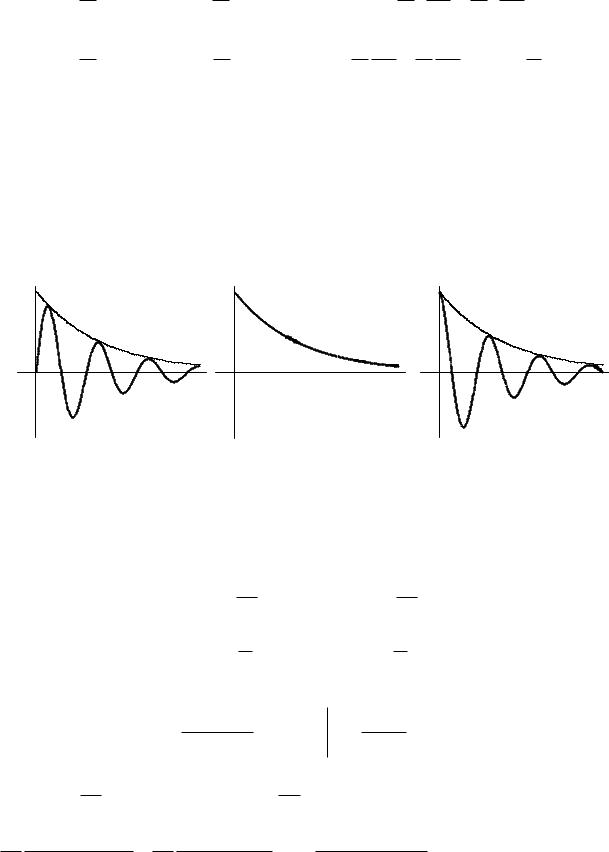
Нарисунке5представ.4 сигналены

s1(t ).

s2 (t )

и s3 (t ),затухающиепо

экспоненциальномузакону

s2 (t )

s1(t )

s3 (t )

закону

Математичемоделисигналовописледующимывакиеобразом: тся

s (t) = Ee−α tσ (t) ;

1

s2 (t) = (Ee

−α t

sinωot)σ (t) =

E

e

−(α − jω

o

)t

σ (t) −

E

e

−(α + jω

o

)t

σ (t);

2 j

2 j

s (t) = (Ee−α t

cosω

o

t)σ (t) = E e−(α − jωo )tσ (t) + E e−(α + jωo )tσ (t).

3

2

2

Определизобтсехажения:гналовм

S ( p) =

∞

Ee−α t e− pt dt =

E

e−(α + p)t

∞

E

;

∫

=

1

− ( p +α)

0

α + p

0

+ E

− E

S2 ( p)

e

−(α − jω

)t

σ

e

−(α + jω

)t

=

= L

2 j

o

(t)

− L

o

σ (t)

2 j

E

1

E

1

ωo

= 2 j ( p + α − jωo ) − 2 j p + α + jωo

= E ( p + α)2 + ωo2 ;

123

S3 ( p)

+ E

e

−(α − jω

)t

+ E

e

−(α + jω

)t

= L

o

σ (t)

+ L

2

o

σ (t)

=

2

=

E

1

+

E

1

= E

p

+ ωo2

.

2 ( p + α − jωo )

2 ( p + α + jωo )

( p + α)2

Представсигнасуммойэкспоненциальныхениеовсоставляющих

привелоксущественномуупрощениюрасчетаизображений.

5.Расчет6.изображений3 поЛапласуодностороннихнезатухающих

гармоническколебанийх

Нарисункепоказаны5.5моделисигналов,представляющихсобой

произведениегармк ническихлеб

анединий ска. чныхков

s1(t )

s4 (t )

E

E

t

t

s2 (t )

s5 (t ) 2E

E

t