Приборы и устройства СВЧ, КВЧ и ГВЧ диапазонов

111

Расположим начало координат в центре зазора первого резонатора, т.е. z = z1 = 0 . На выходе из первого зазора электрон

попадает в пространство дрейфа и движется по инерции, тогда его координата в любой точке z, будет

троном расстояния от средины первого резонатора до точки z от фазы вылета wt1 с первого резонатора. Выражение (5.4) может

быть представлено графически прямыми линиями, угол наклона которых соответствует скорости электронов v . При x1 ¹ 0 угол

наклона прямых изменяется в соответствии с фазой переменного напряжения на зазоре. И чем больше величина x1 , тем больше

изменение угла наклона прямых линий. Тормозящему периоду поля Um1sin(wt1) соответствует меньший угол, ускоряющему —

больший угол наклона прямых. Чем x больше, тем быстрее схо-

дятся траектории, т.е. ускорённые и замедленные электроны сближаются. Такой процесс преобразования электронного потока называется группированием электронов. Пространственно-

временные диаграммы (ПВД) пролетного клистрона ωz = f (ωt1) v0

приведены на рис. 5.2 (прямые зависимости в координатах z=f( wt1 ) . Анализируя графики ПВД, можно сделать интересные

для практики выводы:

1.В некоторой плоскости z = const, где может быть расположен зазор второго резонатора, электронный поток оказался сгруппированным, т.е. приобретает модуляцию по плотности. Глубина этой модуляции зависит от времени пролета в пространстве дрейфа, или от расстояния между модулятором и выходным устройством.

2.Центром группы является электрон, прошедший зазор в нулевой момент переменного поля на зазоре, когда оно изменя-

112

лось от тормозящего к ускоряющему. Эти участки напряжения отмечены жирной чертой на рис. 5.2.

Рис. 5.2 — Пространственно-временные диаграммы

впролетном клистроне

2.Период следования групп электронов (конвекционный ток iк) равен периоду модулирующего напряжения.

3.В группировке участвуют около 50 % непрерывного потока «правильно фазных» электронов.

Получим зависимость угла прибытия электронов в точку z от

параметру М1 ξ1 и ограничимся линейными членами разложения. Получим

Полагая в (5.5а) время средины второго резонатора t = t2 ,

расстояние между срединами резонаторов z = S, обозначая θ — статический угол пролёта невозмущенным электроном пространства дрейфа

получим зависимость фазы прибытия электронов во второй резонатор от фазы вылета из 1-го резонатора в виде

114

ной зависимостью; т.е. в плоскость S прибывает в любой момент времени только одни электрон, вышедший из первого зазора при любой фазе:

б) при Х > 1 в плоскость S = const прибывает в одну и ту же фазу ωt2 − θ уже 3 группы электронов.

в) зазор 1-го резонатора называется фазовой линзой, поскольку он собирает в одну плоскость электроны, проходящие через него в разные фазы переменного напряжения (по аналогии с оптической линзой).

5.3 Конвекционный ток в пространстве дрейфа

В движущейся линейный поток в пространстве дрейфа электроны не вводятся и не выводятся из него, оседанием электронов на идеальных сетках резонатора и попаданием его на стенки трубы дрейфа можно пренебречь. Поэтому воспользуемся законом сохранения заряда для определения величины конвекционного тока на втором резонаторе. Токи в средине первого резонаторе (индекс 1) и в средине второго резонатора (индекс 2) определяются изменением заряда во времени

Конвекционный ток (5.9) с учетом (5.5б) будет равен

115

Выражение (5.10) представлено графически на рис. 5.4 для разных величин Х.

Рис. 5.4 — Конвекционный ток в ПКл для разных Х

При X < 1 ток изменяется почти по гармоническому закону. Если X = 1, знаменатель выражения (5.10) равен нулю при ωt1 = 2πn, где n = 0,1,2.., а ток стремится к бесконечности. При X > 1 знаменатель дважды за период обращается в ноль, т.е. имеются два пика тока в интервале от – π до +π, стремящиеся в бесконечность; с ростом X пики тока расходятся во времени и провал между ними возрастает. Если принять, что M1 ,ξ1 ,ω, v0 —

величины постоянные, а в X (z) = ω z M1U1 изменять только рас- v0 2U0

стояние z, то получим из (5.10) при t1 = const процесс группиров-

ки тока от координаты (рис. 5.5). Таким образом, переменная составляющая конвекционного тока при Х >1 имеет резко несину-

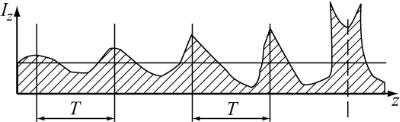
116

соидальный характер, что свидетельствует о богатстве гармониками. Уплотнения тока следуют с частотой модулирующего сигнала.

Рис. 5.5 — Конвекционный ток в пространстве дрейфа при изменении расстояния z

Примечание: Обозначим: электронный ток, поступивший с катода — I0 ; коэффициент прозрачности сеток KC = Sотв / Sсет

— отношение площади отверстий сетки к площади сеточного полотна. Тогда величина тока в средине первого резонатора запи-

В пространстве дрейфа движение электронов идёт по инерции. При значительных плотностях тока существенную роль играют собственные электрические поля групп, приводящие к расталкиванию электронов. В длинных линейных потоках наблюдается два типа разгруппировки: поперечная и продольная. Поперечную разгруппировку электронов устраняют использованием соленоидов (см. гл. 3). Продольную разгруппировку устранить невозможно.

Влияние поля пространственного заряда на конвекцион-

ный ток можно учесть введением поправочного коэффициента в параметр группировки Х.

117

объемная плотность заряда. Преобразуем β p z

г) при 0,8 ≤ b ≤ 1, параметр X ′ = X с точностью 20 %, а оптимальная длина пространства дрейфа, при которой электронный поток будет сгруппирован максимально, лежит в пределах

5.4 Гармонический состав конвекционного тока

Конвекционный ток во втором резонаторе (5.10) — периодическая функция во времени и пространстве. Следовательно, ее можно разложить в гармонический ряд Фурье. Учитывая, что

118

форма тока (рис. 5.4) является четной функцией, можно ограничиться только четными членами ряда Фурье [2].

гральное представление функции Бесселя первого рода n-го порядка при целом n. Тогда

Окончательно разложение мгновенного конвекционного тока во 2-м резонаторе клистрона принимает вид

n=1

Из (5.18) с учетом пространственного заряда (5.11) выражение переменной составляющей конвекционного тока n-ой гармоники во втором резонаторе примет вид

Выводы:

1. Амплитуда n-гармоники конвекционного тока определяется функцией Бесселя (рис. 5.7), зависящей от параметра груп-

119

пировки Х (см. приложение Б) и от величины пространственного заряда (5.19).

2. Максимальные значения функций Бесселя и соответствующие этим значениям параметры группировки для разных гармоник представлены в таблице 5.1. Большое количество гармоник в конвекционном токе говорит о весьма нелинейном процессе группировки.

Рис. 5.7 — Графики функций Бесселя для разных порядков от аргумента X

Таблица 5.1 — Максимальные значения функций Бесселя и соответствующие им Х для разных гармоник n

5.5 Электронный КПД пролетного клистрона

Амплитуда конвекционного тока n-ой гармоники (5.19) при КС = 1 и Х = Х1, т.е. пространственный заряд не учитывается, будет равна I2nk = 2I0 Jn (nX ) . Амплитуда наведенного тока опреде-

120

ляется умножением конвекционного тока на коэффициент взаимодействия электронного потока с переменным электрическим полем второго резонатора на данной гармонике

внешней цепи противоположно направлению конвекционного тока, вызванного движением электронов в зазоре резонатора. Поэтому знак у наведенного тока противоположен знаку конвекционного тока. Электронная мощность n-ой гармоники в выходном резонаторе определяется соотношением

Pэл n = 0, 5U2n I2n cos ψ = −U2n M 2n I0 Jn (nX ) cos ψ , (5.20)

где U2n — амплитуда напряжения n-ой гармоники в выходном зазоре; ψ — фазовый угол между наведенным током и напряже-

нием, созданным в выходном резонаторе.

КПД электронного потока n-ой гармоники определяется соотношением

где P0 = U0 I0 — мощность, подводимая к потоку от постоянного

источника.

Рассмотрим условия, при которых достигается максимальный электронный КПД.

Величина U2nM 2n — амплитуда напряжения n-ой гармони-

ки на выходном зазоре второго резонатора, имеющего нулевую протяженность и расположенного в центре реального зазора, имеет максимальное значение, равное или чуть меньше U0. От-

ношение U2n M 2n = ξ2 ≤ 1 называется коэффициентом использо-

U0

вания постоянного напряжения U0.. Максимальное значение cosψ = −1. С физической точки зрения этот режим ( ψ = π – фазо-

вый угол между наведенным током и напряжением) соответствует прохождению максимального тока в моменты наибольшего тормозящего поля.

Учитывая предельные значения величин в (5.21), получаем