
Модуляция, кодирование и моделирование в телекоммуникационных системах
..pdf
101
Параметр a называется масштабирующим параметром, а параметр b – параметром сдвига.
Результат выполнения вейвлет-преобразования (массив данных, получающийся в результате) полностью зависит от материнского вейвлета.
На практике используются следующие типы вейвлетов:
Вейвлет Хаара.
Мексиканская шляпа.
Модулированная гауссова кривая.
Производная гауссовой кривой.
Вейвлеты Добеши, Грассмана, Мейера.
Вейвлеты Бэттла-Лемарье.
Симлеты.
Койфлеты.
Математический аппарат вейвлета Хаара
Вейвлет Хаара представляет собой следующую функцию:
|
1, (0 |
x |
1 |
) |
||
|
|
|||||
2 |
||||||
(x) |
|
1 |
|
(2.13) |
||
1, ( |
x |
1) |
||||
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
||
Используя в качестве материнской |
функции вейвлет Хаара, можно определить |
|||||
вейвлетные функции.
|
|
r / 2 |
t k 2r |
||
r ,k |
2 |
|
|
|
|
|
|
r |
|||
haar |
2 |
||||
|
|
|
|
|
|
|
(2.14) |
|
|
, r, k Z |
|
|
|
В качестве носителя данная функция имеет интервал длины 2r: |
|
Ir ,k k 2r , (k 1) 2r |
(2.15) |
Большим значениям r соответствуют большие интервалы L, следовательно, вейвлетные функции имитируют большие волны. Одним из примеров, иллюстрирующих применение вейвлетов, является разложение сигнала с помощью выбранного преобразования [5].
Масштабирующая функция имеет вид:
1,0 x 1 |
(2.16) |
(x) |
|
0, x [0,1) |
|
102
Ее интеграл: (x)dx 1.
Масштабирующая функция определяет аппроксимацию сигнала (позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов).
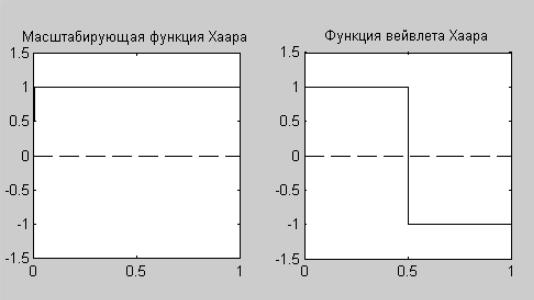
Построение масштабирующей функции и функции вейвлета Хаара представлено на рисунок 2.45.
Рис. 2.45. Масштабирующая функция и функция вейвлета Хаара Преобразование Хаара использует комбинацию этих функций. Чтобы понять, как
выполняется преобразование, выполним сначала преобразование одномерного массива.
Пример. Выполним преобразование Хаара следующего массива:
A = (6, 7, 8, 9, 10, 6, 7, 8).
Вычислим сначала средние и полуразности элементов: 1 шаг:
Средние: (6+7)/2 = 13/2 = 6.5; (8+9)/2 = 8.5; (10+6)/2 = 8, (7+8)/2 = 7.5.
Полуразности: (6-7)/2 = -0.5; (8-9)/2 = -0.5; (10-6)/2 = 2; (7-8)/2 = -0.5
Таким образом, получим массив из восьми элементов:
A1 = (6.5, 8.5, 8, 7.5, -0.5, -0.5, 2, 0.5)
Обратим внимание на последние четыре элемента – их значения гораздо меньше, чем до выполнения преобразования. Поэтому их оставим без изменений. Средние значения называются аппроксимирующими коэффициентами, в которых накапливается максимальная информация, а значения полуразностей позволяют осуществлять полное восстановление

103
исходного сигнала. На следующем шаге мы будем работать с первыми четырьмя элементами, а вторую половину массива оставим без изменений.
2 шаг:
Средние: (6.5+8.5)/2 = 7.5; (8+7.5)/2 = 7,75.
Полуразности: (6.5-8.5)/2 = -1; (8-7.5)/2 = 0.25.
Новый массив: A2 = (7.5, 7.75, -1, 0.25, -0.5, -0.5, 2, -0.5)
3 шаг:
Средние: (7.5+7.75)/2 = 7.625; (-1+0.25) = 0.625.
Полуразности: (7.5-7.75)/2 = -0.125; (-1-0.25)/2 = -0.625.
Новый массив A3 = (7.625, 0.625,-0.125, -0.625, -0.5, -0.5, 2, -0.5)
Из за постоянного вычисления полуразностей происходит постоянное уменьшение значений исходных элементов (пикселей изображения), поэтому после выполнения преобразования, можно к получившемуся массиву дополнительно применить один из алгоритмов сжатия (например, Хаффман или арифметическое кодирование). Если необходимо использовать сжатие с потерями, то здесь используется операция квантования или удаления наименьших значений полуразностей: например, может быть записано: A3 =
(7.625, 0.6250, 0, 0, 0, 2, 0). Тогда исходные данные восстановятся с искажениями.
Рис. 2.46. Результат применения вейвлета Хааара
Математический аппарат вейвлета Добеши
В настоящее время вейвлет Добеши 4-ого порядка является наиболее используемым.
Функция данного вейвлета и его масштабирующая функция представлены на рисунке 2.47.

104
Рис. 2.47. Масштабирующая функция и функция вейвлета Добеши 4-го порядка Масштабирующая функция и функция вейвлета Добеши задаются рекурсивно. Кроме
того, функции удовлетворяют следующему требованию: масштабирующая функция имеет компактный носитель – отрезок [0 3], а также должна быть равна нулю вне этого отрезка.
Эту функцию, как и вейвлет, можно задать рекурсивно, определив начальные условия.
Начальные значения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(0) 0, (1) |
1 3 |
|
, (2) |
1 |
|
3 |
, (3) 0 |
||||||||||||
|
|
|
|
|
|
||||||||||||||
И рекурсивное соотношение: |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(r) |
1 3 |
(2r) |
3 3 |
|
(2r 1) |
3 3 |
|
(2r 2) |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
||
1 
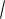 3 (2r 3) 4
3 (2r 3) 4
h0 (2r) h1 (2r 1) h2 (2r 2) h3 (2r 3) (h0 , h1, h2 , h3 ) ( (2r), (2r 1), (2r 2), (2r 3)).
Сумма начальных значений равна единице.
(0) (1) (2) (3) 0 1 
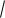 3 1
3 1 
 3 0 1 2 2
3 0 1 2 2
(2.17)
(2.18)
(2.19)
Далее функция вычисляется по шагам. Для этого на шаге 1 применяются условие компактного носителя, начальные значения и рекурсивные соотношения. На последующих шагах также применяется рекурсия. Для построения вейвлета также используется рекурсивное соотношение.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(r) |
1 |
3 |
|
(2r 1) |
|
3 3 |
(2r) |
3 3 |
(2r 1) |
1 3 |
(2r 2) |
(2.20) |
||||||
4 |
|
|
4 |
|
|
4 |
|
|
4 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Использование рекурсивных соотношений при построении вейвлетов и масштабирующих функций способствует тому, что построенные кривые являются

105
самоподобными, то есть обладают фрактальными свойствами. Это делает возможным
применение вейвлетов к анализу фрактальных последовательностей. |
|
|
|
||||||||
Фильтры |
hn n Z |
и |
{gn }n Z вейвлетов |
(x) |
и |
(x) есть |
коэффициенты |
||||
|
(x) |
|
hn (2x n) |
|
|
|
|
||||
масштабирующих уравнений |
2 |
и |
(x) |
2g n (2x n) , где |
|||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gn ( 1)n h N n |
(черта |
обозначает комплексное |
сопряжение). Фильтр |
h называется |
|||||||
низкочастотным, а фильтр g – высокочастотным. Для восстановления используются фильтры и gn вейвлетов и , а для восстановления с помощью фильтров – сопряженные
(транспонированные) фильтры.
Математический аппарат непрерывного вейвлет-преобразования
Запись непрерывного вейвлет-преобразования (НВП) выглядит следующим образом:
(2.21)
|
|
1 |
|
t b |
|||
Wf (a,b) |
|
|
|||||
f (t) |
|
|
|
* |
|
dt |
|
|
|
|
|
||||
|
|
|
s |
|
|
a |
|
|
|
|
|
|
|
|
|
Областью определения вейвлет-преобразования Wf является множество:
R2 _ (a, b) | a R* , b R |
(2.22) |
Параметр a определен в комплексной плоскости, параметр b – в области действительных чисел. В теории вейвлетов ось a масштабируется вертикально, а ось b – горизонтально. Часто область определения Wf ограничивается положительными значениями параметра a.
Главной задачей является нахождение вейвлет-коэффициентов. Использование свойств вейвлет-преобразования позволяет осуществить анализ сигналов. Например, слишком большие амплитуды значений вейвлет-коэффициентов указывают на положение перепадов,
которые имеют резкие изменения интенсивности изображения. Различные масштабы описывают контуры структуры изображения меняющихся размеров. Такое выделение перепадов эффективно для распознавания образов при компьютерной визуализации [4].
Представляется необходимым продемонстрировать действие НВП на примере вейвлета Хаара.
Вейвлет Хаара может быть записан как:
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
1, b t b |
|
|
|
||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
(2.23) |
t b |
|
|
|
|
|
||||
|
a |
|
|
|
|||||
|
|
|
1, b |
|
t b a |
|
|||
|
|
|
|||||||
|
a |
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
106
Вейвлет-преобразование определяется как:
|
|
|
|
|
|
|
|
1 |
|
b a / 2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wf (a, b) |
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
a |
b |
|
||
|
|
|
|
2 b a / 2 |
|
|
|
|
|
|
|||
|
|
a |
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
f (t)dt |
|
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
|
2 a |
b |
|
|
|
|
|
a |
|||||
b a
f (t)dt f (t)dt
|
b a / 2 |
b a |
|
|
|
f (t)dt . |
|
b a / 2 |
|
|
|
|
|
|
|
|
(2.24) |
Это означает, что за исключением нормирующего множителя значение Wf(a,b)
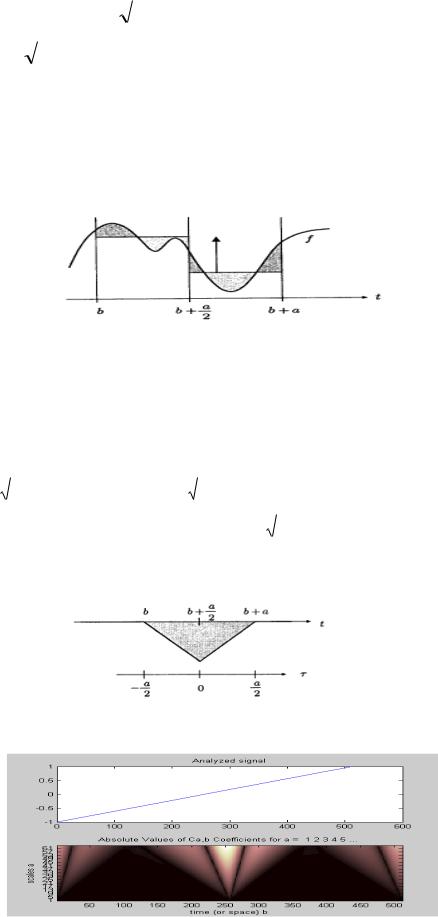
представляет собой разность между двумя средними значениями функции f, эти средние значения берутся по двум соседним интервалам длины a/2 в окрестности точки b.
Рис. 2.48. Результат НВП в случае вейвлета Хаара Величину Wf(a,b) можно рассматривать с другой точки зрения:
|
1 |
|
b a / 2 |
|
a |
|
1 |
|
|||
Wf (a,b) |
|
|
|
|
f (t) f (t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
|
a |
|
a |
|
2 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t a / 2 |
|
|
|
|
|
|
|
|
|
(2.25) |
||
|
|
f |
|
|
|
|
|
|
|
|
|
||
b a / 2 |
' |
(r)dr ... |
|
|
|
||||||||
|
|
|
|
||||||||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
a / 2 a |
|
|
a |
|
||||
b |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
| r | f ' b |
|
r dr |
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
a |
|
2 |
|
|
2 |
|
|||
|
|
|
|
|
|
|
a / 2 |
|
|
|
|
|
|
В этой форме величина Wf(a,b) проявляется как взвешенное среднее производной f’ на интервале [b,b+a].
Рис. 2.49. Другая интерпретация величины Wf
Подставляя вместо f(t) конкретную функцию, можно вычислить ее НВП.
107
Рис. 2.50. Результат НПВ сигнала По полученной спектрограмме можно судить о характере сигнала, например, наблюдать
максимумы «всплесков энергии» в различные промежутки времени (показатель b) и при различных масштабах (показатель a).
Математический аппарат дискретного вейвлет-преобразования
Для обработки и просмотра сигналов и изображений при различных разрешениях также используется дискретное вейвлет-преобразование.
В общем виде прямое дискретное преобразование изображения f(x,y) размерности MxN
можно выразить в общем виде следующим образом:
T (u, v,...) f (x, y)gu,v,... (x, y) |
(2.26) |
|
|
x, y |
|
Здесь x и y – пространственные переменные (координаты пикселей изображения), а u,v –
переменные в частотной области, характеризующие закономерность распределения пикселей изображения. Зная T(u,v…), можно восстановить функцию f(x,y) с помощью обратного преобразования:
f (x, y) T (u, v,...)hu,v,... (x, y). |
(2.27) |
|
|
u,v,.. |
|
Члены последовательностей g и h называются прямыми и обратными ядрами преобразования, определяющими природу, сложность и эффективность пары преобразований. Дискретное вейвлет-преобразование, в отличие от преобразования Фурье,
обозначает целый класс преобразований, которые различаются не только своими ядрами
(коэффициентами), но и свойствами этих коэффициентов (с каким классом вейвлетов мы будем работать) и способом применения этих коэффициентов (сколько требуется вычислить различных решений).
Можно охарактеризовать каждое ДВП с помощью ядра преобразования или, основываясь на множестве параметров, которые однозначно определяют пару ядер. Все преобразования являются родственными (их функции разложения представляют собой «маленькие волны» или «вейвлеты»), которые имеют переменную частоту колебаний и ограниченную длительность.
108
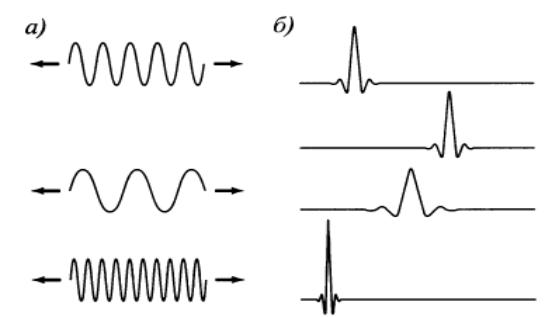
Рис. 2.51. а) Множество функций разложения Фурье – синусоиды с переменной частотой и бесконечной длительностью б) Функции разложения ДВП – «маленькие волны» с
переменной частотой и конечной длительностью Свойства «ядер», являющиеся общими для всех типов вейвлетов.
Свойство 1. Разделимость, масштабируемость и переносимость. Ядра можно представить в виде трех разделимых двумерных вейвлетов:
H (x, y) (x) ( y),
(2.28)
V (x, y) (x) ( y),D (x, y) (x) ( y).
Здесь H (x, y), V (x, y), D (x, y) называются горизонтальными, вертикальными и
диагональными вейвлетами, а двумерная функция: |
|
(x, y) (x) (y) |
(2.29) |
|
Называется масштабирующей функцией. Каждая из этих двумерных функций является
произведением двух одномерных масштабирующих функций [5].
|
j ,k |
(x) 2 j / 2 |
(2 j x k ), |
(2.30) |
|
|
|
||
|
|
|
|
j ,k (x) 2 j / 2 (2 j x k ).
Параметры i и j являются целыми числами. Число k определяет положение одномерных функций на оси x, масштаб j – ширину по оси x, множитель 2j/2 отвечает за высоту и амплитуду.
Свойство 2. Кратномасштабная совместимость. Свойство оговаривает требования к выбранной масштабирующей функции.

109
а) Каждая функция i, j (x) ортогональная любому своему целочисленному сдвигу.
б) Множество функций, которые можно представить в виде рядов разложения по j ,k (x)
при малых масштабах (j мало), принадлежит множеству функций, представимых в более высоких значениях.
в) Каждую масштабирующую функцию можно представить с произвольной точностью
при j . |
|
|
|
Свойство 3. Ортогональность. Функции разложения |
i, j |
x |
образуют ортогональный |
|
|
или биортогональный базис (отсюда и название еще одного типа вейвлетов – ортогональные и биортонональные) в пространстве одномерных измеримых, суммируемых в квадрате функций. Базис обладает тем свойством, что каждая представимая в этом базисе функция имеет единственный набор коэффициентов. Для вещественных ортогональных ядер имеет место равенство g = h. В биортогональном случае
|
|
1, r s. |
(2.31) |
|
hr , gs |
rs |
|
|
|
0 |
|
|||
|
|
|
|
|
Для практического применения важно следствие из приведенных свойств – функцию вейвлета и масштабирующую функцию можно представить в виде линейной комбинации своих же копий с удвоенным разрешением:
|
|
|
(x) h (n) |
|
|
(2.32) |
(x) h (n) |
|
|
2 (2x n) |
|||
2 (2x n), |
|
|||||
n |
|
|
|
|||
n
В среде MATLAB дискретное вейвлет-преобразование реализуется с помощью процедур dwt и fwt (быстрое вейвлет-преобразований). Можно выполнять разложение как двумерных,
так и одномерных сигналов.
Рис. 2.52. Результат дискретного вейвлет-преобразования
110
Алгоритм быстрого вейвлет-преобразования
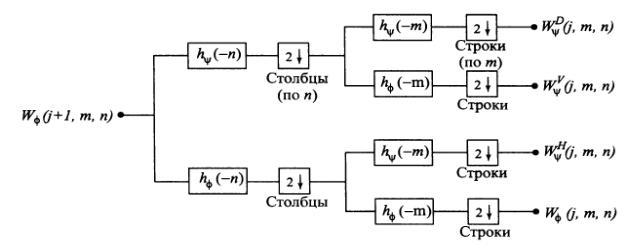
Обобщая преобразование на двумерный и многомерный уровень, можно представить схему преобразования (быстрого вейвлет-преобразования).
Рис. 2.53. Схема быстрого вейвлет-преобразования Сначала обрабатываются столбцы, а затем строки. Используются при этом фильтры
низких и высоких частот.
Каждый проход через блок фильтров на рис. 10 разлагает входные данные на четыре
компоненты меньшего диапазона (или масштаба). Коэффициенты W преобразования
получаются двумя проходами низкочастотной фильтрации (т. е. с фильтром h ), и поэтому
|
W i , i H ,V , D |
|
они называются коэффициентами приближения; коэффициенты |
|
называются, |
|
соответственно, коэффициентами горизонтальных, вертикальных и диагональных деталей.
Поскольку само изображение f(x,y) представлено в наивысшем разрешении, то оно становится входом W ( j 1, m, n) первой итерации процедуры. Кроме того, здесь имеется
три переменные преобразованного пространства: масштаб j, горизонтальная трансляция п и
вертикальная трансляция т. Эти переменные соответствуют обозначениям u,v, … в первых
двух уравнениях (8), (9). Далее посмотрим примеры применения двумерного вейвлет-
преобразования (dwt2, fwt) при обработке изображений.
При выполнении этапов преобразования используется операция свертки сигналов. Слово
«свертка» обозначает совместное сворачивание двух величин или функций [2]. Дискретная
свертка векторов f и g обозначается f*g и вычисляется с помощью соотношения: |
|
|
f g i |
f j gi j |
(2.33) |
|
j |
|
