
Методология системотехнического проектирования электронных и радиоэлектронных средств (в двух частях)
..pdf4.2Основания декомпозиции «черного ящика»
4.2.1Анализ и синтез в исследовании систем
Согласно определениям из системного анализа декомпозиция – это итеративная аналитическая операция разделения целого на части с сохранением признака подчиненности, принадлежности, в результате которой получаются иерархические структуры [1].
Задачу декомпозиции удается решить в случае нахождения ответов на все нижеперечисленные вопросы.
1.Сколько функционально элементарных «черных ящиков» (ЧЯ) существует?
2.Каким образом выполняются операции разделения «черного ящика» как целого на части и как выполняются операции объединения частей в целое?
3.Сколько таких способов существует?
4.Почему операции разделения и объединения выполняются именно таким образом?
Важное значение аналитического метода состоит не только и не столько в том, что сложное целое разделяется на все менее сложные (и в конечном счете простые) части, а в том, что соединенные надлежащим образом эти части снова образуют единое целое. Момент агрегирования частей в целое является конечным этапом анализа, так как лишь после этого можно объяснить целое через его части – в виде структуры целого. При агрегировании следует помнить правило, что вклад любой части в общесистемный эффект зависит от вкладов других частей. Поэтому если заставить каждую часть функционировать наилучшим образом, то в целом эффект не будет наивысшим. Отобрав, например, лучший в мире карбюратор, двигатель, колеса и т.д., мы не только не получим самый лучший автомобиль, но вообще не сможем собрать машину, так как детали машин разных марок не подойдут друг к другу. Итак, при анализе неаддитивных систем следует делать акцент на рассмотрение не отдельных частей, а на их взаимодействия, что является существенно более трудной задачей. Так, управление неаддитивной системой окажется более эффективным, если управлять не действиями её частей отдельно, а взаимодействиями между ними.
Формализация описания любой системы или процесса есть способ упрощения их понимания. То же относится к самому системному анализу и к каждой из используемых в нём операций. К числу наиболее употребительных операций системного анализа принадлежат разделение целого на части и объединение частей в целое. Весьма важнымфактом является то, чтодекомпозиция выполняется посодержательной модели проблеморазрешающей системы. Поэтому качество анализа прямо связано с полнотой используемой модели.
6
4.2.2 Компромиссы между полнотой и простотой анализа «черного ящика»
Сколичественной точки зрения требования к иерархической структуре сводятся
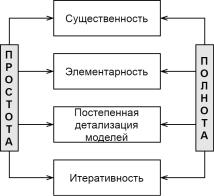
кдвум противоречивым принципам: полноты (проблема должна быть рассмотрена максимально всесторонне и подробно) и простоты (все дерево должно быть максимально компактным – «вширь» и «вглубь»). Компромиссы между ними вытекают из качественного требования – главной цели: свести сложный объект анализа к конечной совокупности простых подобъектов либо (если это не удается) выяснить конкретную причину неустранимой сложности (рисунок 4.1).
Рисунок 4.1 – Схема компромиссов между принципами простоты и полноты анализа
Для поиска баланса междупротиворечивыми требованиями полнотыи простоты необходимо использовать принципы существенности, элементарности, постепенной детализации моделей и итеративности.
Принцип существенности: в модель-основание декомпозиции включаются только компоненты, существенные по отношению к цели анализа (релевантные).
Принцип элементарности: в случае необходимости должна быть возможность продолжения декомпозиции допринятиярешения оеёпрекращении поданной ветви (разные ветви могут иметь различную длину). Такое решение принимается, когда декомпозиция приводит к получению результата (подцели, подфункции, подзадачи и т.п.), не требующего дальнейшего разложения, т.е. результата простого, понятного, реализуемого, обеспеченного, заведомо выполнимого, одним словом, элементарного. Понятие элементарности в системотехнике ЭРЭС базируется на понятии функционального узла, а в схемотехнике – на понятии электронного/радиоэлектронного элемента/компонента принципиальной электрической схемы, работа которого основана на одном или нескольких физических эффектах или явлениях.
Принцип постепенной детализации моделей: если на какой-то ветви дерева не достигается элементарность, товыдвигается предположение, чтодальнейшая декомпозиция может все-таки довести анализ до получения элементарных фрагментов.
7

Возможность продолжения декомпозиции состоит во введении новых элементов в модель-основание и в продолжении декомпозиции по ним.
Принцип итеративности алгоритма декомпозиции придает ему вариабельность, возможность пользоваться моделями различной детальности на разных ветвях, углублять детализацию сколько угодно, если это потребуется.
4.2.3Типы сложности в анализе «черного ящика»
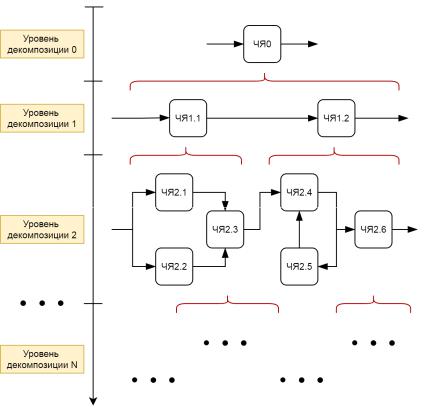
Впроцессе декомпозиции работа специалиста-системотехника может быть осложнена тремя факторами. Соответствующие этим факторам типы сложности проектной ситуации приведены на рисунке 4.2.
Рисунок 4.2 – Типы сложности проектной ситуации
Сложность из-за неинформированности («невежества») заключается в том, что специалист (эксперт) признает недостаточность своей компетентности для дальнейшего анализа. В этом случае ему следует обратиться к эксперту другой квалификации (например, построение новых содержательных моделей требует знаний по иной специальности). Случай, когда декомпозиция заканчивается элементарными фрагментами на всех ветвях дерева, является простейшим. Не имеет значения, один или несколько экспертов довели анализ до конца, важно, что это оказалось возможным, следовательно, первоначальная сложность была вызвана не столько недостатком информации, сколько большой размерностью проблемы.
Сложность из-за непонимания заключается в отсутствии у проектировщика в настоящее время сведений или знаний, необходимых для продолжения процесса декомпозиции «черного ящика». В таком случае анализ не ликвидирует сложность, но локализует её, позволяя определить, каких сведений не хватает на данном шаге декомпозиции.
Сложность из-за незнания заключается в объективном и принципиальном отсутствии на момент декомпозиции «черного ящика» нужных системотехнику научных знаний, что дает ему право ставить перед учеными соответствующих отраслей наук задачи поиска требуемых знаний. В свою очередь наличиеэтогоправа обязывает проектировщика владеть продвинутой способностью формулировать и ставить междисциплинарные задачи.
Таким образом, можно заключить, что метод декомпозиции не дает новых знаний, а лишь «вытягивает» знания из экспертов, структурирует и организует их, обнажая нехватку знаний в виде «дыр» или пробелов в этой структуре. В итоге
8
обнаруженная нехватка конкретных знаний все-таки является новым знанием (раньше нам было неизвестно, что именно мы не знали), а по-иному скомбинированные фрагменты старых знаний также обладают новыми качествами.
4.2.4 От модели «черного ящика» к структурной схеме системы
После того как модель системы типа «черный ящик» разработана, следующими задачами системотехника являются его декомпозиция на «черные ящики» более низкого уровня вплоть до перехода к «функциональным атомам», т.е. неделимым с функциональной точки зрения моделям; их обоснованный выбор; поиск способов связи этих «черных ящиков» друг с другом (рисунок 4.3).
Рисунок 4.3 – Уровни декомпозиции исходного «черного ящика» на примере системы с одним входом и одним выходом (стрелками показаны направления процессов в системе). Уровень декомпозиции N соответствует уровню элементарных функциональных узлов
Если проанализировать данную схему, можно прийти к следующим выводам:
– каждый новый уровень декомпозиции увеличивает количество подсистем, т.е. «черных ящиков» (ЧЯ) n-го уровня декомпозиции;
9
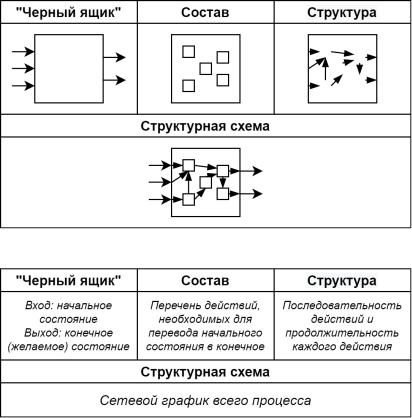
– на последнем уровне декомпозиции все ЧЯ должны быть представлены функционально элементарными частями структуры системы, которые будем называть ФУ.
Далее необходимо найти ответы на следующие вопросы.
Сколько функционально элементарных ЧЯ существует? Чем это определяется? Каково количество ЧЯ каждого типа для ЧЯ0?
Сколько способов соединения ЧЯ друг с другом существует?
Как ЧЯ каждого уровня декомпозиции должны быть связаны друг с другом? По каким правилам они должны соединяться?
В итоге последовательность разработки моделей представлена на рисунке 4.4.
а
б
Рисунок 4.4 – Типы моделей: а – статический вариант; б – динамический вариант
Как было указано в разделе 1, подавляющее большинство ТС организуется из нескольких составляющих (элементов, функциональных узлов, устройств, комплексов, систем) и может быть естественным образом разделено на части. Каждый элемент как самостоятельное ТС выполняет определенную функцию и реализует определенную физическую операцию (ФО), т.е. между элементами имеют место два вида связей и соответственно два вида их структурной организации [2].
10
Элементы, имея определенные функциональные связи друг с другом, образуют
конструктивную функциональную структуру (КФС). КФС представляет собой ориентированный граф, вершинами которого являются наименования элементов, а ребрами – функции элементов.
Кроме функциональных связей, между элементами ТС имеются потоковые связи, т.е. элементы, реализуя определенные физические операции, создают поток преобразуемых или превращаемых веществ, энергии, сигналов или других факторов. Например, на вход источника вторичного электропитания подается переменное напряжение 220 В 50 Гц, а на выходе получается постоянное напряжение 12 В.
Такие потоки определенным образом объединяют и связывают элементы ТО и соответственно их ФО. В сложных ТО часто присутствует несколько взаимосвязанных потоков.
Взаимосвязанный набор ФО, реализующих один определенный поток преобразований вещества, энергии или сигналов, либо несколько взаимосвязанных потоков будем называть потоковой функциональной структурой (ПФС). ПФС представляет собой граф, вершинами которого являются наименования элементов ТО или операций Коллера Е, а ребрами – входные AT и выходные CT потоки (факторы).
Различают две разновидности ПФС: конкретизированную ПФС, у которой в вершинах графа указаны наименования элементов; абстрагированную ПФС, у которой в вершинах графа указаны наименования операций Коллера. Абстрагированную ПФС называют также структурой физических операций.
КФС и ПФС дополняют друг друга. При решении прикладных задач (конструирование, обучение и т.д.) используют или конструктивную ФС, или потоковую ФС, или одновременно обе разновидности.
В потоковой ФС каждый элемент реализует определенную ФО. Такая реализация происходит на основе одного или нескольких физико-технических эффектов
(ФТЭ).
Под ФТЭ будем понимать различные приложения физических законов, закономерностей и следствий из них, физические эффекты и явления, которые могут быть использованы в технических устройствах. Как правило, в ФТЭ имеет место определенная причинно-следственная связь между «входом» и «выходом». ФТЭ должен иметь стандартное формализованное описание, удобное для технических приложений и машинной обработки.
Наиболее обобщенное качественное описание ФТЭ состоит из трех компонен-
тов:
(A, В, C) или Q = ( A B C), |
(4.1) |
где А – входной поток вещества, энергии или сигналов; С – выходной поток; В – физический объект, обеспечивающий или осуществляющий преобразование А в С.
Для входного А и выходного С потоков можно указать носители потоков и их качественные и количественные характеристики. В таблице 4.1 приведены примеры
11

описания ФТЭ по формуле (4.1) для уровня элементов и функциональных узлов
(ФУ).
Таблица 4.1 – Примеры описания физических эффектов
Наименование ФТЭ |
A |
В |
C |
|
элемента или ФУ |
||||
|
|
|
||
Закон Джоуля–Ленца |
Электрический ток |
Проводник |
Теплота |
|
(элемент) |
|
|
|
|
Термоэлектронная |
Теплота |
Оксидная |
Поток электронов |
|
эмиссия |
(нагревание) |
суспензия |
|
|
Пьезоэлектрический |
Деформация (сила) |
Пьезокристалл |
Электрическое |
|
эффект (элемент) |
|
|
поле |
|
Усиление |
Сигнал напряжением |
Усилитель |
Сигнал |
|
напряжения (ФУ) |
U |
с коэф. усиления k |
напряжением kU |
|
Генерация |
Напряжение питания |
Генератор |
Гармонический |
|
гармонического |
|
гармонического |
сигнал |
|
сигнала (ФУ) |
|
сигнала |
|
|
Фильтрация нижних |
Сигнал с произволь- |
Фильтр нижних |
Сигнал со спектром |
|
частот (ФУ) |
ными спектральными |
частот |
в области нижних |
|
|
характеристиками |
|
частот |
4.2.5 Основные физические операции
Важным шагом на пути к методу конструирования структуры систем явился вывод, что процессы в технических системах можно свести к конечному числу элементарных операций. Для определения этих основных операций важнопредставлять, чтов технических системах могут быть только потоки энергий, материалов или сигналов, которые каким-либо образом передаются и/или изменяются (преобразуются) соответствующими системами [3].
В этой связи понятие «сигнал» следует трактовать как прохождение активной физической величины во времени. Причем должны рассматриваться все физические величины, связанные с энергией, или все составляющие энергии, например электрическое напряжение, электрический ток, сила, путь, давление, световой поток, звук и т.д. Активные сигналы представляют собой величины потоков, они могут передаваться из одногоместа в другое. В противоположность им пассивныесигналы не имеют энергии, они не могут передаваться, то есть они прежде преобразуются в активные сигналы. Примерами пассивных сигналов являются картины, формы, переменное электрическое сопротивление и т.д. В этой связи потоки сигналов в первую очередь следует рассматривать как потоки энергии, для конструирования сигнальных устройств содержание информации этих потоков имеет второстепенное значение. Под операцией следует понимать лишь сам процесс, при этом не представляет интереса, что во что должно быть преобразовано. Напротив, под функцией в первую очередь следует понимать связь причины – следствия между входной и выходной величиной, то есть что во что должно быть преобразовано.
12
Таким образом, под физической функцией следует понимать задание, какая физическая величина благодаря какому процессу в какую другую величину должна быть преобразована.
Запись в виде математических символов GA=>GB позволяет выяснить, что, например, энергия вида А должна превращаться в энергию вида B в результате процесса «превращение». Стрелка означает то же самое, что и превращение, она указывает, в результате какого вида деятельности должен быть реализован этот процесс. Стрелку следует рассматривать как операнд функции, подобно тому как знак сложения (+) может быть операндом обычной математической функции, и рассматриваемый сам по себе он не дает никаких сведений о том, какие величины должны суммироваться друг с другом.
Вывод 12 основных физических операций определяется следующими условиями.
1.В технических системах могут изменяться или оставаться неизменными только свойства и состояния энергий, сигналов и веществ. Свойства и состояния энергий и сигналов или их составляющие, например сила, напряжение, электрический ток и т.д., ясно описываются путем указания параметров (единицы измерения, числового значения и направления, если речь идет о векторных величинах,
ичислового значения, если речь идет о скалярных величинах). Таким образом, у физических величин в технических системах может изменяться только единица измерения, числовое значение и направление, других возможностей не существует. Изменение единицы измерения физической величины обычно связано с изменением свойства. Изменение свойств также можно понимать как изменение качества энергии, материала, сигнала или их потоков. Изменение числового значения (количества) физической величины называется изменением состояния. Выражаясь иначе, под изменением состояния следует понимать изменение величины свойства (количества или качества). Отсюда вытекают три основные операции: преобразование, увеличение и изменение направления для энергии, материала и сигнала.
2.Энергияили еесоставляющие, напримерсила, напряжение, электрический ток
ит.д., сигналы и материалы, проходящие через технические системы, формально могут рассматриваться как реки с естественными потоками и аналогичными свойствами:
– существование потока предполагает наличие соответствующего источника и места впадения;
– между источником и местом впадения потоку требуется проводящее пространство;
– поток, расходящийся первоначально во все стороны, может сосредоточиваться (сводиться, собираться) на определенном прямом направлении;
– поток может направляться вдоль заданного пути;
– движение потока может прерываться и снова возобновляться;
– поток в определенной среде может продолжать поступательное движение в одном направлении или колебаться;
– поток в количественном отношении может разделяться или соединяться;
13
–поток, который представляет собой комбинацию из двух или нескольких отдельных потоков, отличающихся физическими характеристиками, согласно этим характеристикам может разделяться;
–поток может накапливаться или выводиться.
Исходя из названных свойств потока и условия, что каждое изменение свойства, отличающееся в качественном отношении, должно соответствовать основной операции, выводятся, в частности, основные семь операций: сбор (концентрация), управление, прерывание, колебание, разделение, разъединение и накопление. Для создания потока формально необходим соответствующий источник и место впадения (следует напомнить о так называемом источнике направления у электрических систем), а также требуется проводимость пространства, находящегося между источником и местом впадения.
С7 названными изменениями свойств потока и с операциями «излучение»
и«проводимость», необходимыми для создания потока, получается 9 основных операций. Вместе с операциями «преобразование», «увеличение» и «изменение направления» получается 12 основных физических операций. Формально каждое изменение свойства, состояния или направления можно сделать обратным, то есть по теоретическим и практическим соображениям к каждой из этих основных операций целесообразно присоединять противоположную операцию, например преобразование – обратное преобразование, увеличение – уменьшение, а изменение направления – последующее изменение направления, которому соответствует переход к первоначальному направлению.
Примерами использования операций «преобразование» и обратное «преобразование» могут служить электрический генератор или электродвигатель. Зубчатая передача представляет превосходный пример реализации операций «увеличение»
и«уменьшение» значения векторной физической величины (число оборотов или крутящий момент) и для изменения направления вектора (угловая скорость).
Каждая основная операция имеет вход и выход. Сообразно этому соответствующие операционные символы имеют две соединительные черты (двухполюсник). Многими из названных основных операций можно управлять посредством вспомогательной величины. Согласно трехполюснику управляемые основные операции должны обозначаться символом с тремя соединительными чертами. Эта возможность управления операцией основывается на том, что они в большинстве случаев реализуются благодаря использованию физических эффектов, закон измерения которых представляет функцию не только одного, а двух или нескольких независимых параметров (y = f (x1; x2; x3;…)), используемых для управления.
Итак, основная операция может иметь один или несколько входов управления (может быть трехполюсником, четырехполюсником или многополюсником).
14
4.2.6 Основные математические операции
Аналогично основным физическим операциям существуют алгебраические операции [3]:
–сложение и вычитание;
–умножение и деление;
–возведение в квадрат и извлечение корня;
–интегрирование и дифференцирование.
Какуфизических, таки уалгебраическихосновныхоперацийимеютсяобратные операции. Поскольку основные алгебраические операции используются в технических системах, имеются устройства, которые выполняют только математические операции. Поэтому их, наряду с основными физическими операциями, целесообразно использовать для синтеза функций технических систем.
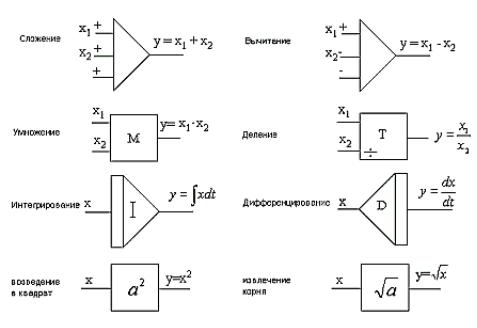
Совокупность этих операций и их символы показаны на рисунке 4.5. В качестве примеров технических устройств, в которых реализованы математическиеоперации, могут служить известные механические настольные счетные машины, планиметры, аналоговые вычислительные машины и т.д.
Рисунок 4.5 – Основные математические операции
15
