Кодирование и шифрование информации в системах связи. Часть 2. Шифрование

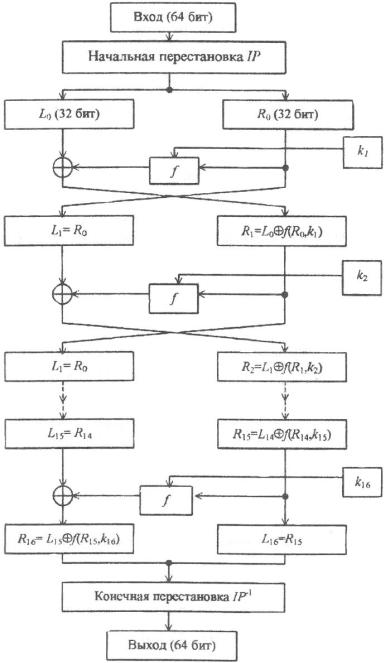
141

Li, Ri – левая и правая половины 64-битового блока;

– операция побитового сложения блоков по модулю 2 (XOR); ki – 48-битовые ключи, получаемые из исходного ключа k;

f – функция шифрования;

IP – начальная перестановка степени 64.

Рис. 2.8. Структура алгоритма DES

Процесс шифрования состоит в начальной перестановке битов 64-битового входного блока, шестнадцати циклах шифрования и, наконец, конечной перестановке битов.

142

Отметим, что все приводимые ниже таблицы являются стандартными и должны использоваться при реализации алгоритма DES в неизменном виде. Все перестановки и коды в таблицах подобраны разработчиками таким образом, чтобы максимально затруднить процесс вскрытия шифра путем подбора ключа.

При зашифровании очередного блока Т (рисунок 4.8) его биты подвергаются начальной перестановке IP согласно приводимой таблице 2.1.

Таблица 2.1. Начальная перестановка IP

При этом бит 58 блока T становится битом 1, бит 50 – битом 2 и т. д. Полученный после перестановки блок IP(T) разделяется на две половины: L0, состоящую из 32 старших бит, и

R0, состоящую из 32 младших бит.

Затем выполняется итеративный процесс шифрования, состоящий из 16 циклов преобразования Фейстеля. Пусть Ti–1 = Li–1Ri–1 – результат (i – 1)-й итерации.

Тогда результат i-й итерации Ti = LiRi определяется формулами

143

Функция f называется функцией шифрования. Ее аргументами являются 32-битовый вектор Ri–1 и 48-битовый ключ ki, который является результатом преобразования 56-битового ключа шифра k. Результатом последней итерации является блок T16 = L16R16. По окончании шифрования осуществляется восстановление позиций битов применением к T16 обратной перестановки IP–1.

При расшифровании данных все действия выполняются в обратном порядке, при этом вместо соотношений (4.2) следует пользоваться соотношениями

пользуясь которыми можно "спуститься" от L16 и R16 к R0 и L0.

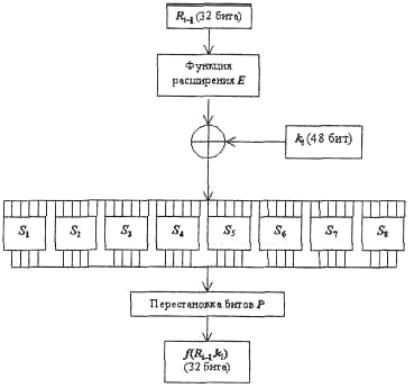
Схема вычисления значения функции шифрования f(Ri–1, ki) изображена на рисунке 2.9.

Рис. 2.9. Схема вычисления функции шифрования f

Для вычисления значения функции f используются:

функция расширения Е;

преобразование S, составленное из восьми преобразований S-блоков S1,

S2, …, S8;

перестановка Р.

Аргументами функции f являются вектор Ri–1 (32 бита) и вектор ki (48 бит). Функция Е

"расширяет" 32-битный вектор Ri–1 до 48-битного вектора E(Ri–1) путем дублирования

144

некоторых битов вектора Ri–1, при этом порядок следования битов в E(Ri–1) указан в таблице

2.2.

Таблица 2.2. Функция расширения E

Первые три бита в E(Ri–1) – это соответственно биты 32, 1 и 2 вектора Ri–1, а последние три бита – это соответственно биты 31, 32, 1 вектора Ri–1.

Полученный результат складывается побитно по модулю 2 с текущим значением ключа ki и затем представляется в виде восьми последовательных 6-битовых блоков B1, B2, …, B8:

E(Ri–1) ki = B1 … B8.

Далее каждый из блоков Bj трансформируется в 4-битовый блок B j с помощью подходящей таблицы S-блока Sj, список которых приведен в таблице 3.

145

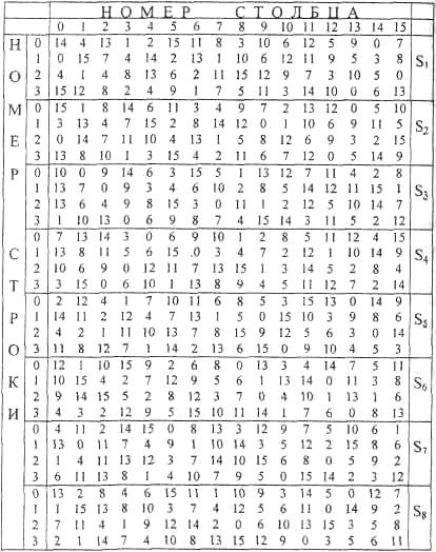
Таблица 2.3. Функция преобразования S

Преобразование блока Bj и B j осуществляется следующим образом. Пусть, например, В2

равен 111010. Первый и последний разряды B2 являются двоичной записью числа a, 0 a 3.

Аналогично средние 4 разряда представляют число b, 0 b 15. В нашем примере a = 2, b = 13.

Строки и столбцы таблицы S2 пронумерованы числами a и b. Таким образом, пара (a, b)

однозначно определяет число, находящееся на пересечении строки с номером a и столбца с номером b. В данном случае это число равно 3. Записывая его в двоичной форме, получаем

B 2, равный 0011.

Значение f(Ri–1, ki) теперь получается применением перестановки битов P, заданной таблицей к результирующему 32-битовому блоку B 1, B 2, …, B 8.

146

Таблица 2.4. Функция P перестановки битов

На каждой итерации используется текущее значение ключа ki (48 бит), получаемое из исходного ключа k следующим образом.

Сначала пользователи выбирают сам ключ k, содержащий 56 случайных значащих битов.

Восемь битов, находящихся в позициях 8,16,...,64, добавляются в ключ таким образом, чтобы каждый байт содержал нечетное число единиц. Это используется для обнаружения ошибок при обмене и хранении ключей. Значащие 56 бит ключа подвергаются перестановке,

приведенной в таблице 2.5.

Таблица 2.5. Функция первоначальной подготовки ключа

147

Эта перестановка определяется двумя блоками C0 и D0 по 28 бит в каждом (они занимают соответственно верхнюю и нижнюю половины таблицы). Так, первые три бита в C0 есть

соответственно 57, 49, 41 биты ключа. Затем индуктивно определяются блоки Ci и Di = 1,16 .

Если уже определены Ci–1 и Di–1, то Ci и Di получаются из них одним или двумя левыми циклическими сдвигами согласно таблице 2.6.

Таблица 2. 6. Таблица сдвигов для вычисления ключа

i

Число сдвигов

Теперь определим ключи ki, 1 i 16. Ключ ki состоит из 48 битов, выбираемых из битов блока CiDi согласно таблице 7. Первыми тремя битами в ki являются биты 14, 17, 11 из блока

CiDi. Отметим, что 8 из 56 бит (с номерами 9, 18, 22, 25, 35, 38, 43, 54) из CiDi отсутствуют в ki.

Таблица 2.7. Функция завершающей обработки ключа

Официально DES являлся стандартом шифрования данных до 31 декабря 1998 г. В 1997

г. был объявлен конкурс на новый стандарт, который был назван AES (Advanced Encryption Standard). 2 октября 2000 г. Национальный институт стандартов и технологий (НИСТ) США объявил победителя конкурса AES. Однако для того, чтобы этот алгоритм завоевал мировое признание, необходимы серьезные исследования его свойств специалистами различных стран.

148

Основные режимы шифрования

Алгоритм DES вполне подходит как для шифрования, так и для аутентификации данных.

Он позволяет непосредственно преобразовывать 64-битовый входной открытый текст в 64-

битовый выходной шифрованный текст, однако данные редко ограничиваются 64 разрядами.

Чтобы использовать алгоритм DES для решения разнообразных криптографических задач, разработаны четыре режимах:

режим электронной кодовой книги (ЕСВ – Electronic Code Book);

режим сцепления блоков шифра (СВС – Cipher Block Chaining);

режим обратной связи по шифртексту (CFB – Cipher Feed Back);

режим обратной связи по выходу (OFB – Output Feed Back).

Лабораторная работа №1

Изучение стандарта криптографической защиты AES (Advanced Encryption Standart)

Цель работы

Ознакомиться с криптографическим стандартом шифрования AES и его особенностями,

изучить различными режимами блочного шифрования.

Краткие теоретические сведения

Историческая справка

В 1997 г. Национальный институт стандартов и технологий США (NIST) объявил о начале программы по принятию нового стандарта криптографической защиты - стандарта

XXI в. для закрытия важной информации правительственного уровня на замену существующему с 1974 г. алгоритму DES, самому распространенному криптоалгоритму в мире.

Требования к кандидатам были следующие:

криптоалгоритм должен быть открыто опубликован;

криптоалгоритм должен быть симметричным блочным шифром, допускающим размеры ключей в 128, 192 и 256 бит;

криптоалгоритм должен быть предназначен как для аппаратной, так и для программной реализации;

149

криптоалгоритм должен быть доступен для открытого использования в любых продуктах, а значит, не может быть запатентован, в противном случае патентные права должны быть аннулированы;

криптоалгоритм подвергается изучению по следующим па раметрам: стойкости,

стоимости, гибкости, реализуемости в smart-картах.

В финал конкурса вышли следующие алгоритмы: MARS, TWOFISH и RC6 (США),

RUNDAEL (Бельгия), SERPENT (Великобритания, Израиль, Норвегия). По своей структуре

TWOFISH является классическим шифром Фейстеля; MARS и RC6 можно отнести к модифицированным шифрам Фейстеля, в них используется новая малоизученная операция циклического "прокручивания" битов слова на число позиций, изменяющихся в зависимости от шифруемых данных и секретного ключа; RUNDAEL и SERPENT являются классическими

SP-сетями. MARS и TWOFISH имеют самую сложную конструкцию, RUNDAEL и RC6 -

самую простую.

В октябре 2000 г. конкурс завершился. Победителем был признан бельгийский шифр

RIJNDAEL, как имеющий наилучшее сочетание стойкости, производительности,

эффективности реализации и гибкости. Его низкие требования к объему памяти делают его идеально подходящим для встроенных систем. Авторами шифра являются Йон Дэмен (Joan Daemen) и Винсент Рюмен (Vincent Rijmen), начальные буквы фамилий которых и образуют название алгоритма - RIJNDAEL.

После этого NIST начал подготовку предварительной версии Федерального Стандарта Обработки Информации (Federal Information Processing Standart - FIPS) и в феврале 2001 г.

опубликовал его на сайте http://csrc.nist.gov/encryption/aes/. В течение 90-дневного периода открытого обсуждения предварительная версия FIPS пересматривалась с учетом комментариев, после чего начался процесс исправлений и утверждения. Наконец 26 ноября

2001 г. была опубликована окончательная версия стандарта FIPS-197, описывающего новый американский стандарт шифрования AES. Согласно этому документу стандарт вступил в силу с 26 мая 2002 г.

Блочный криптоалгоритм RIJNDAEL и стандарт AES

Высочайшую надежность AES NIST подтверждает астрономическими числами.

128битный ключ обеспечивает 340 андециллионов (340*1036) возможных комбинаций, а 256битный ключ увеличивает это число до 11*1076. Для сравнения, старый алгоритм DES,

150

дает общее число комбинаций в 72*1015 На их перебор у специально построенной машины

"DES Cracker" уходит несколько часов. Но даже если бы она делала это всего за одну секунду, то на перебор 128битного ключа машина потратила бы 149 триллионов лет. Межу тем, возраст всей Вселенной ученые оценивают в менее, чем 20 миллиардов лет.

Математические предпосылки

Алгоритм оперирует байтами, которые рассматриваются как элементы конечного поля

GF(28).

Элементами поля GF(28) являются многочлены степени не более 7, которые могут быть заданы строкой своих коэффициентов. Если представить байт в виде

b7, b6, b5, b4, b3, b2, b1, b0,

то элемент поля описывается многочленом с коэффициентами из {0, 1}:

b7 х7 + b6 х6 + b5 х5 + b4 х4 + b3 х3 + b2 х2 + b1 х1 + b0

Например, байту {11001011} (или {cb} в шестнадцатеричной форме) соответствует многочлен х7 + х6 + х3 + х + 1.

Для элементов конечного поля определены аддитивные и мультипликативные операции.

Сложение

Сложение суть операция поразрядного XOR и поэтому обозначается как . Пример выполнения операции сложения:

(х6 + х4 + х2 + х + 1) (x7 + х+ 1) = х1 + х6 + х4 + х2 (в виде многочленов)

{01010111} 0 {10000011} = {11010100} (двоичное представление)

{57} {83} = {d4} (шестнадцатеричное представление)

В конечном поле для любого ненулевого элемента а существует обратный элемент -а,

при этом а + (-а) = 0, где нулевой элемент -это {00}. В GF(28) справедливо а + а = 0, т. е.

каждый ненулевой элемент является своей собственной аддитивной инверсией.