Кодирование и шифрование информации в системах связи. Часть 1. Кодирование

111

В результате выполнения операции получается один вектор, охватывающий диапазон входного сигнала. Поэтому вейвлет-преобразования называют поддиапазонными.

Дискретная свертка двух числовых последовательностей f(i) и g(i) задается неравенством:

h(i) f (i) g(i) f (i)g(i j)

j

Свертка сигналов применяется, например, для удаления шума или сглаживания сигналов.

Использование приложения Wavelet Toolbox Matlab для сжатия информации путем вейвлет-преобразований [12] .

Пакет MATLAB Wavelet Toolbox представляет собой совокупность программ,

позволяющих выполнять вейвлет-анализ и обработку сигналов средствами графического интерфейса пользователя. Пакет позволяет продемонстрировать практические приложения теории вейвлетов и вейвлет-преобразований. Остановимся на следующих пунктах:

1.Просмотр вейвлетов.

2.Одномерный дискретный вейвлет-анализ.

2.1.Вейвлет-разложение сигнала.

2.2.Интерпретация статистических характеристик сигнала.

2.3.Гистограммы коэффициентов аппроксимации и детализации.

3.Сжатие одномерных сигналов.

4.Удаление шума из сигналов.

Главное меню пакета вызывается из MATLAB с помощью команды wavemenu.

112

Рис. 2.54. Главное окно Wavelet Toolbox

Способы просмотра вейвлетов в Wavelet Toolbox

Способы просмотра вейвлетов – группа Display (кнопка Wavelet Display). Откроется следующее окно:

Рис. 2.55. Окно раздела Wavelet Display после запуска

Вверху расположено обычное меню, справа и внизу – меню, позволяющие управлять отображением нужной информации.

В правом меню можно из раскрывающегося списка тип вейвлета, задать уровень разрешения (параметр Refinement)

– определить шаг вычисления значений вейвлетов (этот параметр равен 1/2N, N по умолчанию равно 8).

Также можно посмотреть информацию по выбранному типу вейвлета.

Выбрав из списка тип вейвлета ‘haar’, следует нажать кнопку Display(Refinement = 8).

Рис. 2.56. Вейвлет и масштабирующая функция Хаара, фильтры восстановления и разложения

113

Вверху расположены графики масштабирующей функции и функции вейвлета. Ниже

изображены фильтры восстановления и разложения вейвлета (низкочастотные и

высокочастотные). Для восстановления используются фильтры (коэффициенты масштабирующих уравнений) h и g функций (x) и (x) , а для вейвлет-разложения – сопряженные (транспонированные) фильтры. Это хорошо видно на графиках фильтров. Для вейвлета Хаара фильтры простые, так как базовыми операциями являются нахождение средних и полуразностей. У других вейвлетов фильтры более сложные по своей структуре.

Например, если выбрать вейвлет Добеши 7-ого порядка, то получится следующее изображение:

Рис. 2.57. Вейвлет 7-го порядка и масштабирующая функция Добеши, фильтры восстановления и разложения

Сжатие сигналов при помощи вейвлет-преобразований в Wavelet Toolbox

В главном окне необходимо нажать кнопку Wavelet 1-D, появится диалоговое окно,

интерфейс которого позволяет осуществлять обработку одномерных сигналов.

Загрузка сигнала Frequency Breakdown (Load Example Analysis  Basic Signals  Frequency Breakdown):

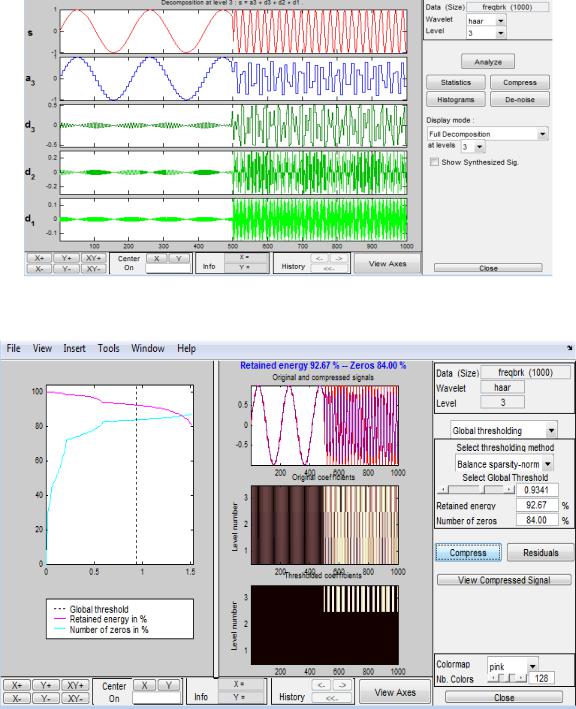
114

Рис. 2.58. Разложение сигнала

Кнопка compress позволяет осуществить сжатие одномерного сигнала.

Рис. 2.59. Интерфейс окна, вызываемого нажатием кнопки Compress

При сжатии одномерных сигналов используется метод глобальной пороговой обработки детализирующих коэффициентов. Управлять сжатием можно группой компонентов справа, устанавливая ползунком значение. Задав порог (процент сохраняемых коэффициентов), в результате получается сжатый сигнал.

115

Рис. 2.60. Исходный и сжатый сигнал при помощи вейвлет-преобразования Хаара

третьего уровня

Сжатие одномерного сигнала при помощи различных вейвлет-преобразований

На сегодняшний день существует большое количество математических алгоритмов вейвлет-преобразований, данный раздел содержит рассмотрение трех основных и сравнительный анализ их характеристик.

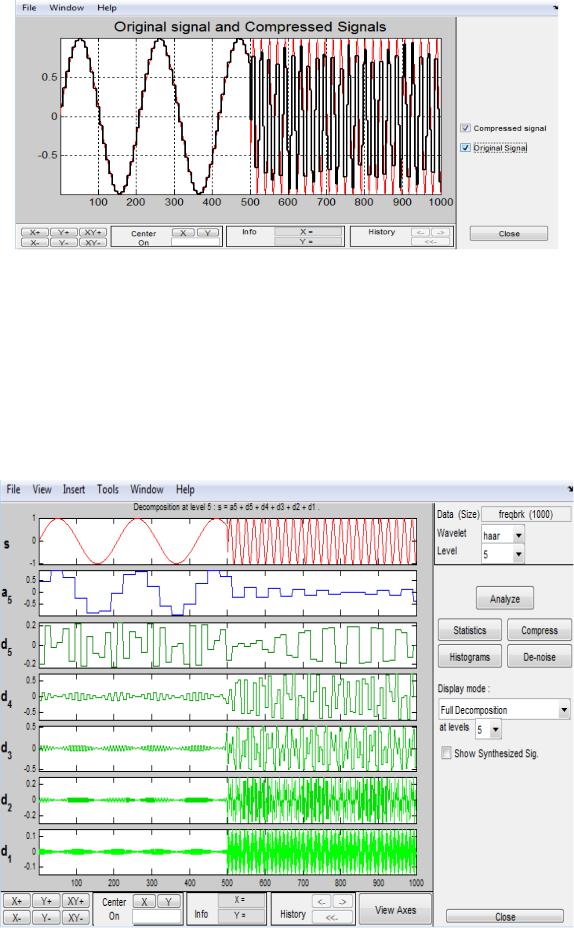
Вейвлет Хаара пятого уровня. Разложение исследуемого сигнала при помощи вейвлета Хаара пятого уровня представлено на рисунке 2.61

Рис. 2.61. Разложение сигнала при помощи вейвлета Хаара пятого уровня

116

Рис. 2.62. Сжатие сигнала при помощи вейвлета Хаара пятого уровня

Рис. 2.63. Исходный и сжатый сигнал при помощи вейвлет-преобразования Хаара пятого уровня при коэффициенте сжатия 0.98

117

Далее необходимо проанализировать зависимость количества сохраненной энергии

сигнала от коэффициента сжатия, результаты представлены в таблице 2.7.

Таблица 2.7. Зависимость количества сохраненной энергии от коэффициента сжатия для вейвлет-преобразования Хаара пятого порядка

Данную зависимость удобно представить в виде графика (рисунок 2.64):

Рис. 2.64. Зависимость количества сохраненной энергии от коэффициента сжатия для вейвлет-преобразования Хаара пятого уровня

Вейвлет Добеши пятого уровня и пятого порядка. Разложение исследуемого сигнала при помощи вейвлета Добеши пятого уровня и пятого порядка представлено на рисунке 2.65.

Рис. 2.65. Разложение сигнала при помощи вейвлета Добеши пятого уровня и пятого порядка

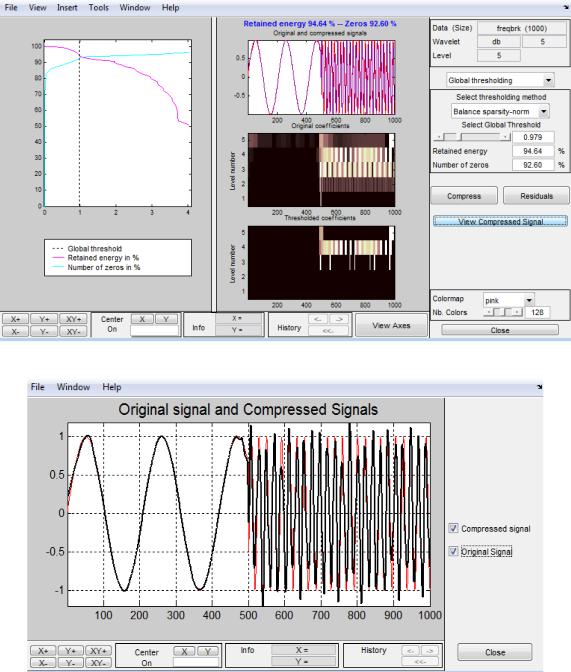
118

Рис. 2.66. Сжатие сигнала при помощи вейвлета Добеши пятого уровня и пятого порядка

Рис. 2.67. Исходный и сжатый сигнал при помощи вейвлет-преобразования Добеши

пятого уровня и пятого порядка при коэффициенте сжатия 0.98

Далее необходимо проанализировать зависимость количества сохраненной энергии

сигнала от коэффициента сжатия, результаты представлены в таблице 2.7

Таблица 2.7 – Зависимость количества сохраненной энергии от коэффициента сжатия для вейвлет-преобразования Добеши пятого порядка

119

Рис. 2.68. Зависимость количества сохраненной энергии от коэффициента сжатия для вейвлет-преобразования Добеши пятого уровня и пятого порядка

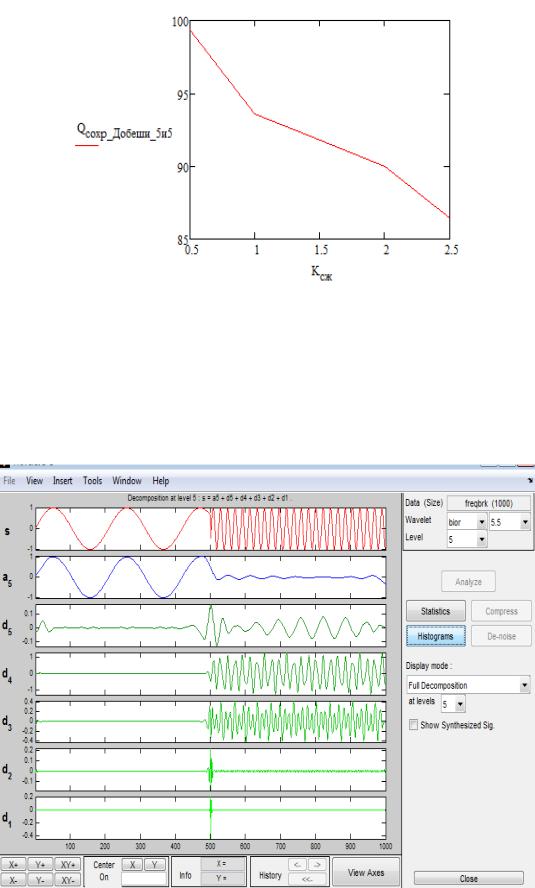
Биортогональное преобразование пятого уровня и порядка 5,5. Разложение исследуемого сигнала при помощи биортогонального преобразования пятого уровня и порядка 5,5

представлено на рисунке 2.70.

Рис. 2.70. Разложение сигнала при помощи биортогонального преобразования пятого уровня и порядка 5,5

120

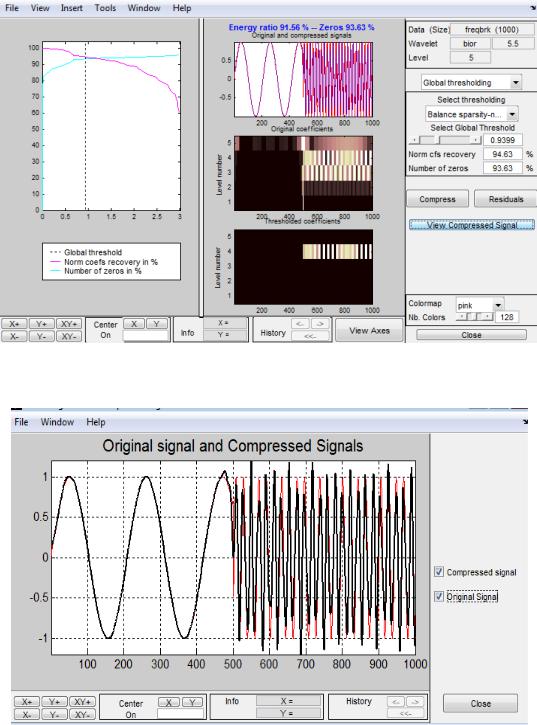
Рис. 2.71. Сжатие сигнала при биортогональном вейвлет-преобразовании пятого уровня и порядка 5,5

Рис. 2.72. Исходный и сжатый сигнал при помощи биортогонального вейвлет-

преобразования пятого уровня и 5,5 порядка при коэффициенте сжатия 0.98

Далее необходимо проанализировать зависимость количества сохраненной энергии

сигнала от коэффициента сжатия, результаты представлены в таблице 2.8.

Таблица 2.8. Зависимость количества сохраненной энергии от коэффициента сжатия для вейвлет-преобразования Хаара пятого порядка