Введение в современную теорию поляризации радиолокационных сигналов. Том 1. Поляризация плоских электромагнитных волн и её преобразования

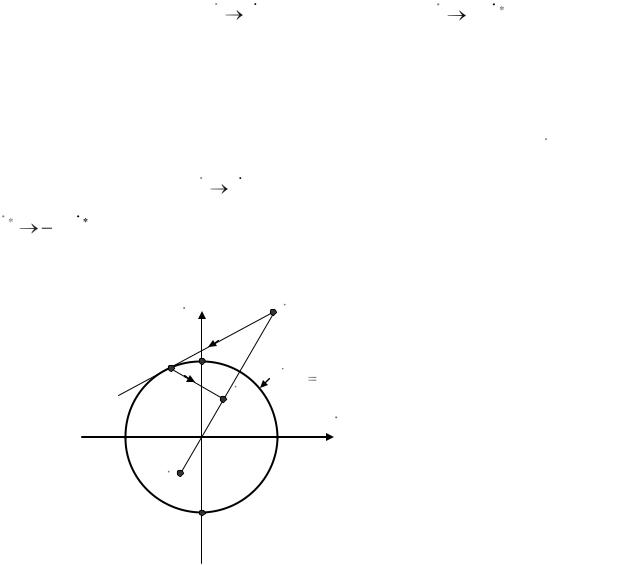
Вторая точка пересечения этой хорды с построенной окружностью будет

представлять точку, изображающую ортогональную поляризацию.

В связи с этим целесообразно воспользоваться более простой процедурой построения изображения поляризации, ортогональной к некоторой заданной

поляризации. Как показано на Рис. 1.12, точка Р, изображающая заданную

поляризацию, прежде всего инвертируется относительно единичной

окружности. Процессу инверсии P PI отвечает замена P 1/ P . Для геометрического построения инвертированной точки необходимо провести из точки Р (см Рис.1.12) касательную к единичной окружности, а затем из точки касания Т опустить перпендикуляр на прямую, соединяющую точку Р с

PORT

L

Fig. 1.12

1.6. Круговое поляризационное отношение и представление состояний

поляризации на круговой комплексной плоскости.

71

Если в качестве базисных состояний используются правая и левая круговые поляризации, а поляризационное отношение образовано проекциям вектора Джонса волны на орты кругового базиса, то комплексная плоскость, точкам которой отвечают значения данного поляризационного отношения, называется круговой комплексной плоскостью [14].

Используя выражение (1.45) для вектора Джонса в круговом поляризационном базисе

Из соотношения (1.65b) следует, что модуль кругового поляризационного отношения непосредственно связан с углом эллиптичности эллипса поляризации, а аргумент этого отношения представляет собой удвоенное значение азимутального угла эллипса:

72

Поскольку каждому комплексному числу P RL может быть сопоставлена точка комплексной плоскости PRL Re PRL Im PRL , то эта комплексная

плоскость может рассматриваться как еще один вариант пространства

состояний поляризации. Это пространство, каждая точка которого взаимно-

однозначно связана с множеством комплексных чисел, отвечающих значения поляризационного отношения в круговом поляризационном базисе,

представляет собой так называемую круговую комплексную плоскость, в

отличие от декартовой комплексной плоскости, использующей линейный поляризационный базис и линейное поляризационное отношение.

Свяжем с началом координат круговой комплексной плоскости точку PRL 0 .

Эта точка соответствует круговой поляризации с левым направлением

вращения (угол эллиптичности 0.25 ). Тогда бесконечно удаленная

точка будет соответствовать круговой поляризации с правым направлением

значение угла эллиптичности, расположены на единичной окружности

аргумент кругового поляризационного отношения определяет ориентацию

линейно-поляризованной волны в пределах 0.5 0.5 . (Этот эффект

обсуждался при анализе представления линейно поляризованной волны с произвольной ориентацией её электрического вектора суммой двух колебаний,

поляризованных по правому и левому кругу.

Все прочие точки круговой комплексной плоскости отображают

73

Графическое изображение круговой комплексной плоскости приведено на Рис.

оканчивающиеся в бесконечно удаленной точке. При этом любая бесконечная прямая, проведенная через начало координат, содержит два луча, разделенные началом координат (левая круговая поляризация) и бесконечно удаленной точкой (правая круговая поляризация). Эти лучи представляют собой линии постоянных азимутов для ортогональных азимутальных углов. При переходе через начало координат или через бесконечно удаленную точку азимут скачкообразно изменяется на величину 0.5 . Как уже отмечалось, ориентация для круговых поляризаций не определена.

Im PRL

Fig. 1.13

Если построить на круговой комплексной плоскости семейство концентрических окружностей с центром в начале координат, то эти

окружности будут представлять собой линии постоянной эллиптичности. При

74

этом семейство линий постоянной эллиптичности ортогонально семейству линий постоянного азимута (см. Рис.1.13).

Декартова и круговая комплексная плоскость представляют собой только два элемента из возможной группы представлений состояний поляризации точками комплексной плоскости. В общем случае комплексное поляризационное отношение может быть задано в произвольном эллиптическом поляризационном базисе, а его значениям могут быть сопоставлены точки некоторой комплексной плоскости, называемой обобщенной комплексной плоскостью. Эта плоскость и её свойства будут рассмотрены ниже.

В заключение настоящего подраздела необходимо указать, что в подразделах 1.1 – 1.6 были рассмотрены различные методы, которые могут быть использованы для представления состояний поляризации: геометрическое представление, представление вектором Джонса, представление параметрами Стокса, представление на сфере Пуанкаре, представление на комплексной плоскости. Однако, представления состояний поляризации с использованием параметров Стокса и сферы Пуанкаре не были достаточно обоснованы и их связь с другими методами представления не была проанализирована детально.

В связи с этим следующий подраздел, посвященный математическому анализу связи между единичной сферой и комплексной плоскостью, будет логическим завершением методов представления состояния поляризации.

1.7. Стереографическая проекция и сферическое представление состояний

поляризации.

Первоначальное определение поляризационной сферы (сферы Пуанкаре)

было введено в подразделе 1.2 с использованием нормированного вектора

Стокса

S 1;cos 2 cos 2 ;cos 2 sin 2 ;sin 2 ,

75

Уравнения стереографической проекции, связывающей точку на комплексной плоскости с координатами её сферического изображения, имеют вид [18]:

чисел или сферой Римана [18]. При этом поверхность сферы имеет смысл

77

поляризационного пространства, каждая точка которого однозначно соответствует некоторому состоянию поляризации.

Рассмотрим теперь основные свойства этого пространства, которые графически иллюстрируются на Рис.1.14б. Прежде всего, отметим, что южный полюс, касающийся начала координат круговой комплексной плоскости,

отвечает левой круговой поляризации, поскольку начало координат проецируется само в себя. Бесконечно удалённая точка плоскости проецируется на северный полюс сферы, который, таким образом, служит изображением правой круговой поляризации.

При диаметре сфере равном единице, единичная окружность на круговой комплексной плоскости, содержащая точки, отвечающие всем линейным поляризациям, проецируется на экватор.

За исключением полюсов экватора все остальные точки сферы являются отображением точек, отвечавших эллиптическим состояниям поляризации на круговой комплексной плоскости.

При этом точки нижней полусферы связаны отображением P PS с

точками, заключёнными внутри единичной окружности на комплексной плоскости и, следовательно, соответствуют поляризациям с левым направлением вращения. Соответственно, точки, лежащие вне единичной окружности и отвечающие правому направлению вращения поляризации,

отображаются на верхнюю полусферу.

Рис.1.14б

Рассмотрим теперь отображение линий постоянного азимута и постоянной эллиптичности круговой комплексной плоскости на поверхность

сферы.

Как было указано в разделе 1.6, линией постоянного азимута является луч, исходящий из начала координат и заканчивающийся в бесконечно удалённой точке. Этот луч представляет собой половину бесконечной прямой

азимутальному углу β отвечает луч, ориентированный под углом 2β на комплексной плоскости. Каждый луч постоянного азимута отображается на линию меридиана (долготы) сферы, заключённую между северным и южным полюсами. При этом, поскольку ориентация луча постоянного азимута определяется удвоенным азимутальным углом, то и угловая долгота

соответствующего меридиана сферы равна удвоенному азимуту эллипса поляризации.

Вторая половина бесконечной прямой, проведённой через начало координат (луч ортогональных азимутов) отображается на меридиан,

диаметрально противоположный первому. Таким образом, при переходе через

полюса сферы азимут эллипса поляризации изменяется скачком на / 2 . За

начало отсчёта азимутов на сфере будем считать точку, соответствующую поляризации с нулевым азимутом. Азимут положителен, когда он

против часовой стрелки / 2 0 . Направление определяется, глядя на

сферу со стороны северного полюса вдоль полярной оси.

Линии постоянной эллиптичности, представляющие собой семейство концентрических окружностей на круговой комплексной плоскости,

проецируется на сферу в виде семейства коаксиальных широтных окружностей.

Их общей осью является полярная ось. Для определения соотношения между угловой широтой и углом эллиптичности воспользуемся рис.1.15 на котором изображено сечение сферы плоскостью, проходящей через оба, полюса и произвольную точку Р круговой комплексной плоскости [14].

Рис. 1.15

Расстояние от начала координат до точки Р на комплексной плоскости определяется модулем поляризационного отношения в круговом базисе и

т.е. удвоенному углу эллиптичности. Широта положительна выше экватора