
Физика
..pdf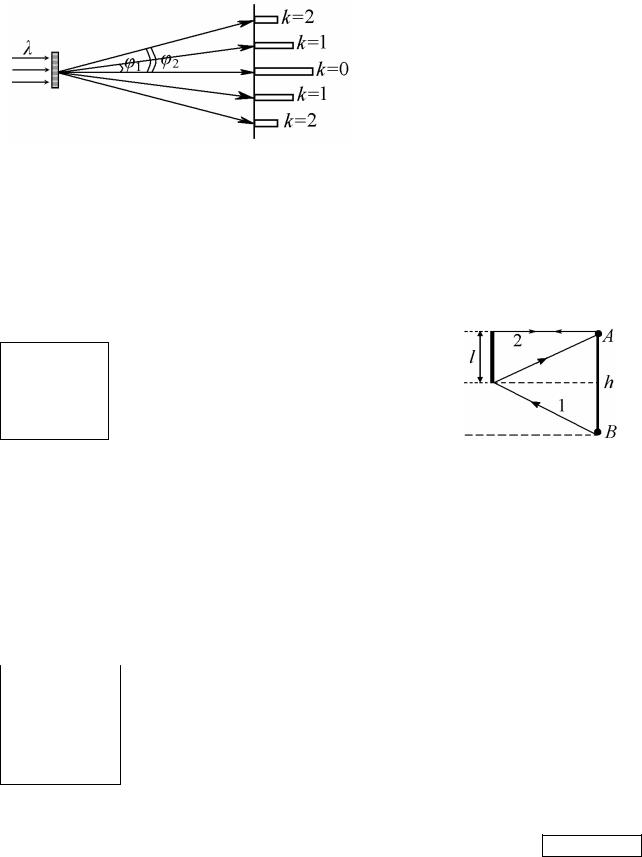
Рисунок 10.11 – Дифракция света на решётке
где d – период решетки; λ – длина волны света в среде, окружающей решетку; k – номер максимума (порядок дифракции); φk – угол дифракции, определяющий направление на максимум с номером k. Дифракционный максимум нулевого порядка (k = 0) носит название главного (центрального) максимума.
10.6.ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1.Плоское зеркало подвешено на вертикальной стене. Человек ростом 170 см стоит перед зеркалом. Какой минимальной высоты в сантиметрах должно быть зеркало, чтобы человек видел свое изображение во весь рост?
Решение:
Условию задачи удовлетворяет построение хода лучей, приведенное на рис. 10.12. Человек видит себя в зеркале полностью только тогда, когда в его глаз (точка А) приходят, испытав
отражение, лучи, исходящие как от самой нижней точки человека (точка В), так и от самой верхней
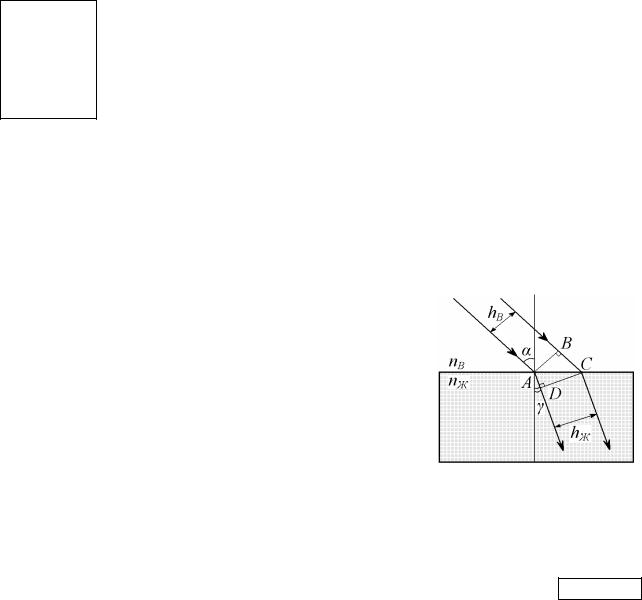
(точка А). Из рисунка видно, что это возможно при высоте зеркала l, не меньшей, чем половина высоты человека h, причем удаленность человека от зеркала
не играет роли. Итак, l = h/2 = 1,7/2 = 0,85 м = 85 см. |
l = 85 см. |
2. Частота световой волны равна 500 ТГц. Определить на сколько длина этой волны в вакууме больше чем в среде с показателем преломления равным 1,2. Ответ дать в нанометрах.
Решение:
Дано: |
Скорость света в вакууме c = λ0ν, где λ0 – длина волны в ва- |
|
кууме. Отсюда имеем: λ0 = с/ν. Скорость света той же частоты ν |
||
14 |
||
ν = 5∙10 Гц |
в некоторой среде v = λν, где λ – длина световой волны в этой |
|
n = 1,2 |
оптической среде. Абсолютный показатель преломления среды |
|
Найти: |
||
определяется соотношением n = с/v = с/λν, откуда находим |
||
|
λ= ? (нм) λ = c/nν. Записываем выражение для изменения длины волны:
λ= λ0 – λ = c(n – 1)/nν. Проведём расчёты и получим:
λ= 3∙108∙(1,2 – 1)/1,2∙5∙1014 = 6∙107/6∙1014 = 1∙10–7 м = 100 нм.
λ= 100 нм.
3.Распространяющийся в жидкости луч света падает на плоскую поверхность стекла. Синус угла падения равен 0,8. Угол между отражённым от стекла и преломлённым в стекле лучами прямой. Определить абсолютный показатель преломления стекла, если абсолютный показатель преломления жидкости равен 1,2.
211
Решение:
Ход лучей изображен на рис. 10.3. Запишем закон преломления света при падении его на границу раздела жидкость-стекло: sinα/sinγ = nC/nЖ. Отсюда найдем показатель преломления стекла: nC = nЖ∙sinα/sinγ. Tак как угол между лучами 1' и 2 – прямой, на-
ходим связь между углом падения α и углом преломления γ:
γ = 90° – α. Тогда sinγ = sin(90° – α) = cosα = (1 – sin2α)1/2. В окон-
чательном виде результат имеет вид: nC = nЖ∙sinα/(1 – sin2α)1/2. Подставляя чис-
ленные значения, будем иметь: nC = 1,2∙0,8/(1 – 0,64)1/2 = 1,6. |
nС = 1,6. |
4. Пучок параллельных лучей света падает на плоскую поверхность жидкости. Угол падения равен 60°, косинус угла преломления равен 0,7. Ширина пучка в воздухе равна 5 мм. Найти ширину пучка в жидкости. Ответ дать в миллиметрах.
Решение: |
На рис. 10.13. показан ход двух |
||||
Дано: |
|||||
лучей, которые ограничивают по- |
|||||
α = 60o |
|||||
cosγ = 0,7 |
перечное |
сечение |
пучка. Из |
гео- |
|
метрических соображений следует, |
|||||
–3 |
|||||
hВ = 5∙10 м |
что BAC = α, |
ACD = γ. Рас- |
|||
Найти: |
сматривая |
прямоугольные |
тре- |
||
hЖ = ? (мм) |
|||||
угольники ABC и ADC, замечаем, |
|||||
|
|||||
что косинусы углов падения и преломления можно выразить через ширину пучка в соответствующей среде: cosα = AB/AC = hB/AC, cosγ = CD/АС = hЖ/АС.
Поделив эти два выражения друг на друга, приходим к соотношению cosα/cosγ = hВ/hЖ. Откуда получаем для ширины пучка света в жидкости: hЖ = hВ∙cosγ/cosα. После расчётов, получим hЖ = 5∙10–3∙0,7/0,5 = 7∙10–3 м = 7 мм. hЖ = 7 мм.
5. Предельный угол полного отражения для стекла, помещенного в жидкость с показателем преломления 1,25, равен 30°. Определить скорость света в этом стекле. Ответ дать в километрах в секунду.
Решение:
Дано: |
Ход лучей при падении света на границу раздела двух опти- |
||||
ческих сред под предельным углом внутреннего отражения αпр |
|||||
αпр = 30o |
|||||
nЖ = 1,25 |
изображен на рис. 10.4. Скорость света в стекле vC входит в |
||||
определение абсолютного показателя |
преломления стекла: |
||||
Найти: |
|||||
nC = с/vC, откуда vC = с/пС. Чтобы найти показатель преломле- |
|||||
vC = ? (км/с) |
|||||
|
ния стекла, запишем условие полного внутреннего отражения: |
||||
|
|||||
sinαпр = nж/nC, |
откуда nC = nж/sinαпр. Сделав подстановку и вычислив, имеем: |
||||
vC = с∙sinαпр/пЖ = 3∙108∙0,5/1,25 = 1,2∙108 м/с = 1,2∙105 км/с. |
|
vС = 1,2∙105 км/с. |
|
||
212
6. С помощью линзы, оптическая сила которой 4 диоптрии, наблюдают увеличенное в 5 раз мнимое изображение предмета. На каком расстоянии перед линзой поместили этот предмет? Ответ дать в единицах СИ.
Решение:
Увеличенное мнимое изображение может быть получено только при помощи собирающей линзы (рис. 10.9, а). Запишем формулу тонкой линзы: 1/F = 1/d + 1/f. Поскольку изображение находится с той же стороны, что и предмет, расстояние f < 0. Введем в рассмотрение также оптическую силу линзы D = 1/F. С учетом этого формула линзы перепишется: D = 1/d – 1/f. По оп-
ределению увеличение линзы Г = | f |/d, откуда | f | = Гd. Подставляем модуль расстояния | f | в формулу тонкой линзы и находим расстояние d = (Г – 1)/DГ.
Вычисляя, получим: d = (5 – 1)/4∙5 = 1/5 = 0,2. |
d = 0,2 м. |
7. Фокусное расстояние собирающей линзы 10 см, расстояние от предмета до ее переднего фокуса 5 см. Найти высоту предмета, если высота его изображения 4 см. Ответ дать в сантиметрах.
Решение:
При указанном положении предмета создаваемое линзой изображение – действительное (рис. 10.8.). Из подобия треугольников на этом рисунке для увеличения линзы Г = H/h получаем еще одно полезное выражение Г = f /d (здесь f > 0). Таким образом, имеем: h = H∙(d/f). Чтобы найти отношение расстояний d/f, запишем формулу тонкой линзы 1/F = 1/d + 1/f. Умножив это уравнение на величину d, найдем: d/f = d/F – 1. Теперь учтем,
что расстояние от предмета до линзы d = l + F. Итак, d/f = l/F. Окончательно для высоты предмета получаем: h = H∙ (l/F) = 0,04∙(0,05/0,1) = 0,02 м = 2 см.
h = 2 см.
8. Сходящийся пучок лучей падает на рассеивающую линзу таким образом, что продолжения падающих лучей пересекаются в точке, лежащей на оптической оси линзы на расстоянии 15 см от нее. Найти фокусное расстояние линзы, если после преломления в линзе лучи собираются в точке, находящейся на расстоянии 60 см от линзы. Ответ дать в единицах СИ.
Решение:
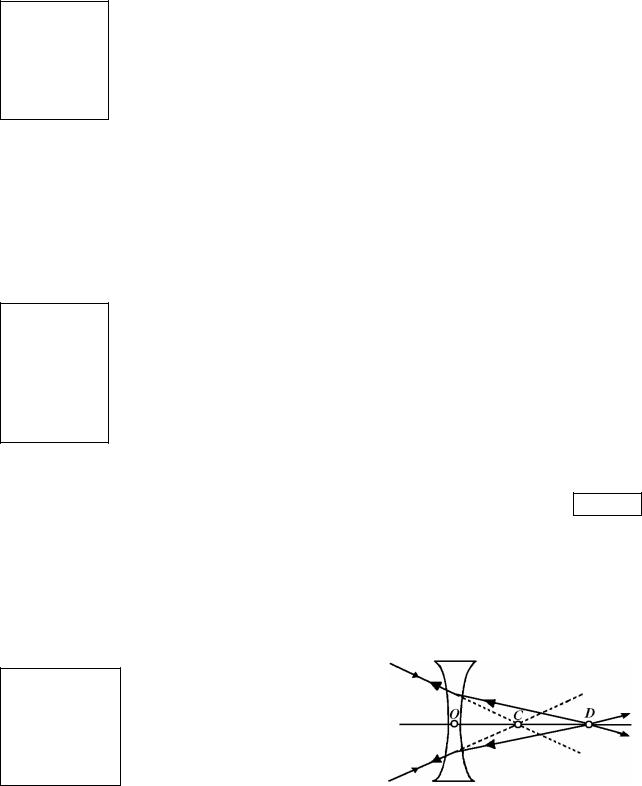
Геометрия задачи изображена на рис. 10.14. Идея решения заключается в том, чтобы развернуть ход лучей в обратном направлении (показано большими стрел-
ками). При этом развернутые лучи пойдут по тому же самому пути. А это равносильно то-
му, что в точку D мы поместили точечный источник света. Следовательно, в точке С находится его мнимое изображение. Итак, теперь OD – расстояние от
213
источника до линзы (OD – d), а ОС – расстояние от линзы до его изображения (ОС – | f |). Запишем формулу рассеивающей линзы: 1/F = 1/d – 1/| f |. Отсюда легко находим фокусное расстояние линзы: F = | f |d/(| f | – d) = 0,15∙0,6/(0,15 –
0,6) = 0,09/(– 0,45) = – 0,2 м. |
F = 0,2 м. |
9. На дифракционную решётку, имеющую одинаковую ширину непрозрачных промежутков и прозрачных щелей, равную 1200 нм, нормально падает свет с длиной волны 500 нм. Определить наибольший порядок максимума, который наблюдается для данной длины волны.
Решение:
Дано: |
Запишем условие максимумов для дифракции света на ре- |
|||
шётке: d∙sinφk = kλ. Величина левой части ограничена, так как |
||||
a = b |
||||
максимальное значение функции sinφk = 1. Следовательно, |
||||
a = 1,2∙10–6 м |
||||
λ = 5∙10–7 м |
ограничена |
по величине и правая часть этого равенства: |
||
Найти: |
d∙1 = kmax∙λ, |
откуда kmax = d/λ. Учитывая, |
что период дифрак- |
|
ционной |
решётки d = а + b = 2а, в |
итоге получаем: |
||
kmax = ? |
||||
kmax = 2а/λ = 2∙1,2∙10–6/5∙10–7 = 4,8. Порядок максимума дол- |
||||
|
||||
|
||||
жен быть целым числом. Однако полученное численное значение kmax нельзя округлять в большую сторону, чтобы исходное равенство не нарушалось. От-
брасывая дробную часть, получаем окончательный ответ kmax = 4. |
kmax = 4. |
10. На дифракционную решетку падает нормально поток белого света. В направлении, определяемом углом 30°, для длины волны 450 нм наблюдается максимум пятого порядка. Определить синус угла, в направлении которого для длины волны 600 нм наблюдается максимум третьего порядка.
|
Решение: |
Запишем условие максимумов для дифракции на решётке |
|||||
Дано: |
|||||||
двух световых волн с длинами λ1 и λ2: |
d∙sinφk1 = k1λ1 и |
||||||
φ1 = 30° |
|||||||
d∙sinφk2 = k2λ2. Поделив почленно одно уравнение на другое, |
|||||||
λ1 |
–7 |
||||||
= 4,5∙10 м |
получаем отношение: sinφk1/sinφk2 = k1λ1/k2λ2. Отсюда следует |
||||||
k1 |
= 5 |
выражение для синуса угла, под которым наблюдается мак- |
|||||
λ2 |
= 6∙10–7 м |
||||||
k2 |
= 5 |
симум с k2 = 3: sinφk2 = sinφk1∙(k2λ2/k1λ1). Численный расчет да- |
|||||
–7 |
/5∙4,5∙10 |
–7 |
) = 0,4. |
||||
Найти: |
ёт следующий результат: sinφk2 = 0,5∙(3∙6∙10 |
|
|||||
|
|
sinφk2 = 0,4. |
|||||
sinφk2 = ? |
|
|
|||||
|
|
|
|
|
|||
214
10.7. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задачи 3 класса трудности
3.1.На дифракционную решётку, период которой равен 2000 нм, нормально падает свет с длиной волны 500 нм. Определить, под каким углом наблюдается второй максимум интенсивности света (k = 2). Ответ дать в градусах.
3.2.Луч света падает на плоскую поверхность озера. После преломления в
воде направление луча изменилось на 8 . Определить в градусах угол преломления, если угол падения равен 30 .
3.3.Луч света падает на плоское зеркало перпендикулярно его плоскости. Зеркало повернули на 30 . Найти в градусах угол между падающим и отражённым лучами после поворота зеркала.
3.4.Свет, распространяющийся в воде падает на плоскую поверхность
стекла. Угол падения равен 30 , синус угла преломления равен 0,4. Определить относительный показатель преломления стекла.
3.5.Угол падения света на плоскую поверхность стекла равен 40 , угол преломления 30 . Определить в градусах наименьший угол между отражённым
ипреломлённым лучами.
3.6.На дифракционную решётку нормально падает свет с длиной волны 520 нм. Третий максимум интенсивности света наблюдается под углом, синус которого равен 0,4. Найти в нм постоянную дифракционной решётки.
3.7.Луч света распространяется из стекла с показателем преломления 1,5 в воду с показателем преломления 1,35. Найти синус предельного угла полного отражения света.
3.8.Предмет находится на расстоянии 0,4 м от собирающей линзы. Действительное изображение предмета получается на экране, удалённом от линзы на расстояние 0,5 м. Найти в СИ оптическую силу линзы.
3.9.Луч света падает на пластинку под углом 18 . Найти в градусах наименьший угол между продолжением падающего луча и отражённым лучом.
3.10.Луч света падает из стекла с абсолютным показателем преломления 1,5 в стекло с абсолютным показателем преломления 1,8. При этом угол пре-
ломления равен 30 . Определить синус угла падения.
3.11. На дифракционную решётку, период которой равен 5000 нм, нормально падает свет с длиной волны 500 нм. Определить номер максимума интенсивности света, который наблюдается под углом 30 . Номер центрального максимума считается равным k = 0.
3.12. В сосуд из стекла с абсолютным показателем преломления 1,5 налита жидкость. В жидкости распространяется свет, угол падения которого на дно сосуда равен 30 , а синус угла преломления в стекле 0,4. Определить абсолютный показатель преломления жидкости.
3.13.Определить в градусах предельный угол полного отражения для стекла с показателем преломления 2.
3.14.Свет с длиной волны 550 нм падает нормально на плоскую дифракционную решётку, период которой равен 2000 нм. Определить синус угла, под которым наблюдается второй дифракционный максимум (k = 2).
215
3.15.Свет с длиной волны 500 нм нормально падает на плоскую дифракционную решетку. Под углом 30 наблюдается третий дифракционный максимум (k = 3). Найти в нм период дифракционной решётки.
3.16.Световые лучи падают нормально на плоскую дифракционную решётку, период которой равен 2500 нм. Синус угла, под которым наблюдается третий дифракционный максимум (k = 3), равен 0,6. Найти в нм длину волны световых лучей.
3.17.Свет, распространяющийся в вакууме, падает на плоскую поверх-
ность стекла под углом 30 . Определить абсолютный показатель преломления стекла, если синус угла преломления светового луча равен 0,25.
3.18.Луч света падает на поверхность стеклянной пластины так, что угол между падающим и преломлённым лучами равен 150 . Угол падения равен 62 . Определить в градусах угол преломления.
3.19.На поверхность прозрачной жидкости падает тонкий луч света, при
этом угол между падающим и преломлённым лучами равен 153 . Определить в градусах угол падения, если известно, что угол преломления равен 32 .
3.20. Луч света падает из стекла с абсолютным показателем преломления 1,8 в жидкость с абсолютным показателем преломления 1,5. При этом угол падения равен 30 . Определить синус угла преломления.
3.21.Тонкий луч света падает на плоскую поверхность стеклянной пластины под некоторым углом. Определить показатель преломления стекла, если синус угла падения равен 0,75, а синус угла преломления равен 0,5.
3.22.Лунный луч падает на поверхность озера под углом 50 к горизонту. Определить в градусах угол между падающим и отражённым лучами.
3.23.Свет с длиной волны 600 нм падает нормально на дифракционную решётку, период которой равен 18000 нм. Определить синус угла, под которым будет наблюдаться третий дифракционный максимум (k = 3).
3.24.Луч света падает на поверхность прозрачной жидкости. При этом
угол между падающим и преломлённым лучами равен 160 , угол падения равен 60 . Определить в градусах угол преломления.
3.25.Фотограф снимает автомобиль в тот момент, когда тот проезжает мимо него на малой скорости. При длине автомобиля 4 м его изображение на плёнке равно 0,032 м. Найти в СИ расстояние от автомобиля до линзы объектива, если расстояние от линзы до фотоплёнки равно 0,06 м.
3.26.Определить в диоптриях оптическую силу собирающей линзы, если расстояние от предмета до линзы равно расстоянию от линзы до действительного изображения и составляет 0,4 м.
3.27.Свет, распространяясь в среде с показателем преломления равным 2, на границе с вакуумом испытывает полное внутреннее отражение. Найти минимальное значение синуса угла падения светового луча на указанную границу.
3.28.Найти показатель преломления материала иллюминатора самолета относительно воздуха, если световой луч падает на иллюминатор под углом
30 , а значение синуса угла преломления светового луча при этом равно 0,4.
216
3.29.Расстояние между предметом и его действительным изображением равно 1,2 м. Найти увеличение, даваемое линзой, если расстояние от предмета до линзы равно 0,4 м.
3.30.Расстояние между свечой и её мнимым изображением на экране равно 0,9 м. Найти увеличение, даваемое линзой, если расстояние от линзы до свечи равно 0,3 м.
3.31.На горизонтальном столе лежит шар. Под каким наименьшим углом к плоскости стола нужно установить зеркало, чтобы при движении шара к зеркалу по столу изображение шара двигалось по вертикали. Ответ дать в градусах.
3.32.Монохроматический плоскопараллельный пучок света нормально падает на дифракционную решётку с периодом 8 мкм. Первый дифракционный максимум наблюдается под углом, синус которого равен 0,05. Определить в мкм длину волны света.
3.33.Найти в нм период дифракционной решётки, если четвёртый макси-
мум для длины волны 600 нм наблюдается под углом 30 ?
3.34.Какой по счёту максимум, не считая центральный, будет наблюдаться под углом 30 для длины волны света 0,6 мкм, падающего на дифракционную решётку с периодом 4,8 мкм?
3.35.Свет распространяется в среде с абсолютным показателем преломления, равным 1,5. Определить в км/с скорость света в данной среде.
3.36.Найти показатель преломления среды, скорость света в которой равна
1,5 105 км/с, относительно среды, скорость света в которой 2,7 105 км/с.
3.37.Плоское зеркало поворачивается на угол 30 . На какой угол повернется отражённый от зеркала луч? Ответ дать в градусах.
3.38.Предмет находится на расстоянии 10 м от рассеивающей линзы. Мнимое изображение наблюдается на расстоянии 2,5 м от линзы. Определить в СИ оптическую силу линзы.
3.39.Определить линейное увеличение, которое даёт лупа с оптической силой 20 диоптрий. Расстояние наилучшего зрения принять равным 25 см.
3.40.Угол падения светового луча на границу раздела двух сред равен 60 . Преломлённый луч составляет с нормалью угол 40 . Определить в градусах наименьший угол между отражённым и преломлённым лучом.
3.41.Угол падения луча света на поверхность стекла равен 56 . Определить в градусах угол преломления, если отражённый и преломлённый лучи взаимно перпендикулярны.
3.42.Фокусное расстояние рассеивающей линзы равно -0,5 м, мнимое изображение находится на расстоянии 0,3 м от линзы. Определить в СИ расстояние от линзы до предмета.
3.43.Скорость света в жидкости в 1,25 раза больше, чем в стекле. Определить абсолютный показатель преломления стекла, если абсолютный показатель преломления жидкости 1,4.
3.44.Абсолютный показатель преломления стекла 1,6. Абсолютный показатель преломления алмаза 2,4. Во сколько раз скорость света в стекле больше скорости света в алмазе?
217
3.45.Под каким углом падает луч на плоское зеркало, если отражённый луч перпендикулярен падающему? Ответ дать в градусах.
3.46.Действительное изображение свечи находится на расстоянии 3 м от собирающей линзы. Фокусное расстояние линзы 1,5 м. Определить в СИ расстояние между линзой и свечой.
3.47.Луч света проходит через границу раздела двух сред. Синус угла падения равен 0,6, а синус угла преломления 0,4. Абсолютный показатель преломления первой среды равен 1,2. Найти абсолютный показатель преломления второй среды.
3.48.Луч света проходит из одной среды в другую. Скорость света в пер-
вой среде 2,75 105 км/с, а во второй 2,5 105 км/с. Определить относительный показатель преломления этих сред.
3.49. Луч падает на зеркальную поверхность так, что угол между лучом и поверхностью равен 35 . Определить в в градусах угол отражения этого луча.
3.50.Мнимое изображение свечи находится на расстоянии 3 м от собирающей линзы. Фокусное расстояние линзы 1,5 м. Определить в СИ расстояние между линзой и свечой.
3.51.Найти в СИ фокусное расстояние линзы, если расстояние от предмета до линзы равно 0,4 м, а расстояние от линзы до действительного изображения составляет 1,2 м.
3.52.Какое линейное увеличение дает лупа с оптической силой 20 диоптрий? Расстояние наилучшего зрения принять равным 0,25 м.
3.53.Свет с длиной волны 600 нм нормально падает на плоскую дифракционную решётку. Синус угла падения, под которым наблюдается пятый дифракционный максимум, равен 0,4. Найти в нм период дифракционной решётки.
3.54.Свет с длиной волны 625 нм нормально падает на плоскую дифракционную решётку, период которой равен 2500 нм. Найти синус угла, под которым наблюдается второй дифракционный максимум.
3.55.Луч света, распространяющийся в среде с показателем преломления 1,8, падает на границу раздела со средой, показатель преломления которой 1,2. Найти синус угла преломления, если синус угла падения равен 0,3.
3.56.Световой луч падает на границу раздела двух сред под углом 40 . Преломлённый луч отклоняется от направления падающего луча на 10 . Найти
вградусах угол преломления, если среда, в которой распространяется преломлённый луч, оптически более плотная.
3.57.Оптическая сила лупы равна 10 дптр. Найти линейное увеличение, даваемое лупой, если расстояние наилучшего зрения равно 0,25 м.
3.58.Луч света падает на поверхность прозрачной жидкости. При этом
угол между падающим и преломлённым лучами равен 160 , угол падения равен 60 . Определить в градусах угол преломления.
Задачи 4 класса трудности
4.1. Призма с показателем преломления 1,6 и преломляющим углом 30 находится в вакууме. Найти синус угла падения луча из вакуума на первую
218
преломляющую грань призмы, если на вторую преломляющую грань луч падает внутри призмы перпендикулярно грани.
4.2. Длина волны света в вакууме = 600 нм. Этот свет входит в некоторую среду, где его скорость уменьшается в 1,2 раза, а длина волны становится равной . Определить в нм разницу ( ).
4.3. На дифракционную решётку нормально падает свет, длина волны которого 600 нм. Второй максимум интенсивности света (k = 2) наблюдается под углом 30 . Найти в мкм период дифракционной решётки.
4.4. В стеклянный сосуд с горизонтальным плоским дном налита жидкость, показатель преломления которой 1,5. На поверхность жидкости под некоторым углом (sin = 0,75) падает тонкий луч света. Найти в градусах наименьший угол между лучом света и дном сосуда в точке падения луча на дно.
4.5. Призма изготовлена из стекла с показателем преломления 1,4. Луч света падает на одну из преломляющих граней призмы перпендикулярно. Найти синус угла преломления при выходе луча света в вакуум через вторую преломляющую грань, если преломляющий угол призмы равен 30 .
4.6.Свет переходит из жидкости с показателем преломления 1,5 в стекло. При этом длина волны света уменьшилась в 1,2 раза. Определить абсолютный показатель преломления стекла.
4.7.Определить в нм длину волны света в жидкости с показателем преломления 1,4. Известно, что длина волны этого света в вакууме равна 602 нм.
4.8.Луч света, распространяющийся в жидкости, падает на стекло под не-
которым углом (sin = 0,8). Угол преломления равен 30 . Определить во сколько раз скорость света в стекле меньше, чем в жидкости.
4.9.Точечный источник света и два его изображения, даваемые плоскими двумя зеркалами, лежат в вершинах равностороннего треугольника. Определить в градусах величину угла между зеркалами.
4.10.На дифракционную решётку с шириной непрозрачных промежутков 2000 нм и шириной прозрачных щелей 2500 нм нормально падает поток белого
света. Найти в нм длину волны света, для которой под углом 30 наблюдается максимум третьего порядка.
4.11.Луч света, проходя через малое отверстие в тонкостенном шаре, испытывает двукратное отражение от его зеркальной внутренней поверхности и выходит через это же отверстие наружу. Найти в градусах угол между входящим в шар световым лучом и радиусом шара, проведённым в точку первого отражения луча.
4.12.Для света с частотой 5 1014 Гц абсолютный показатель преломления некоторой жидкости равен 1,25. Найти в мкм длину волны света в этой жидкости.
4.13.Определить в км/с скорость распространения света в кристалле, если известно, что при синусе угла падения светового луча на плоскость кристалла,
равном 0,75, угол преломления равен 30 .
4.14. На полу стоит квадратный стол со стороной 0,7 м и высотой 0,6 м. Над центром стола на высоте 2 м от пола висит лампочка. Определить в СИ площадь тени стола на полу.
219
4.15.Найти в СИ расстояние от изображения до линзы, если фокусное расстояние линзы 0,6 м, а расстояние от предмета до линзы 0,9 м.
4.16.Угол падения луча света на плоское дно стеклянного сосуда с жидко-
стью равен 30 . Синус угла преломления светового луча в стекле равен 0,25. Определить, во сколько раз скорость света в жидкости больше, чем в стекле.
4.17.Расстояние от предмета до собирающей линзы 10 м, а от линзы до изображения 2,5 м. Определить в диоптриях оптическую силу линзы.
4.18.Чтобы измерить высоту столба, мальчик положил на землю плоское зеркальце так, чтобы видеть в нём изображение вершины столба, и сделал необходимые измерения. Расстояние от него до столба 4 м, до зеркальца 1 м, линия глаз мальчика находится на высоте 1,5 м над Землёй. Определить в СИ высоту столба.
4.19.Фокусное расстояние собирающей линзы равно 0,2 м. Расстояние от линзы до предмета 0,25 м. Найти в СИ расстояние от линзы до изображения.
4.20.На горизонтальном дне водоёма глубиной 1,5 м лежит плоское зеркало. На каком расстоянии от места вхождения луча в воду он снова выйдет из
воды после отражения от зеркала, если угол преломления этого луча в воде 45 ? Ответ дать в СИ.
4.21.Предмет находится на расстоянии 3 см от собирающей линзы с оптической силой 25 дптр. Определить в см расстояние от изображения до линзы.
4.22.Собирающая линза даёт на экране чёткое изображение предмета, находящегося на расстоянии 20 см от линзы. Определить в СИ фокусное расстояние линзы, если расстояние между предметом и экраном равно 50 см.
4.23.Световая волна с частотой 5 1014 Гц распространяется в прозрачной среде. Длина волны 400 нм. Определить показатель преломления среды.
4.24.Предмет помещён перед передним фокусом линзы на расстоянии 25 см до него. Изображение получается за задним фокусом линзы на расстоянии 36 см от него. Определить в см фокусное расстояние линзы.
4.25.На дифракционную решётку нормально падает монохроматический свет. На бесконечно большом экране, установленном за дифракционной решёткой параллельно ей, наблюдается 7 максимумов интенсивности света. Определить наибольший порядок дифракции k, наблюдаемый при данных условиях.
4.26.Лучи от удалённого источника света падают на рассеивающую линзу параллельно её главной оптической оси. Мнимое изображение источника света находится на расстоянии 0,2 м от линзы. Найти в СИ оптическую силу линзы.
4.27.Световой луч, распространяющийся в жидкости со скоростью
2,4 105 км/с, падает на стекло под углом, синус которого равен 0,6. Абсолютныйпоказатель преломления стекла равен 1,5. Определить в градусах угол преломления.
4.28. В сосуд из стекла с абсолютным показателем преломления 1,5 налита жидкость. В жидкости распространяется свет, угол падения которого на дно сосуда равен 30 , а синус угла преломления в стекле 0,4. Определить абсолютный показатель преломления жидкости.
4.29. На дифракционную решётку падает нормально монохроматический свет. Наибольший порядок дифракции k, наблюдаемый при данных условиях,
220
