
Физика
..pdf
мальное сопротивление шунта, если внутреннее сопротивление миллиамперметра 8 Ом.
7.7. Электрическая лампа сопротивлением 240 Ом рассчитана на напряжение 120 В. Для того, чтобы её включить в сеть 220 В, к ней последовательно присоединяют резистор, выполненный из нихромовой проволоки сечением 0,2 мм2. Удельное сопротивление нихрома 1 мкОм м. Определить в СИ длину проволоки.
7.8. От генератора с э.д.с. 40 В и внутренним сопротивлением 0,04 Ом ток поступает к месту сварки по медному кабелю сечением 170 мм2, удалённому на 50 м от генератора. Найти в СИ напряжение на сварочном аппарате, если ток в цепи 200 А. Удельное сопротивление меди принять равным 1,7 10–8 Ом м.
7.9.Можно ли две лампочки мощностью 35 Вт и 75 Вт, рассчитанные на напряжение 127 В, включить последовательно в сеть с напряжением 220 В, если допустимое перенапряжение не более 10%? Если да, то ответ 1, если нет, ответ 0.
7.10.Нагревательный элемент термостата, состоящий из двух одинаковых
параллельно соединённых спиралей, подключается к источнику тока с внутренним сопротивлением 10 Ом. Каким должно быть сопротивление каждой спирали, чтобы при перегорании одной из них это не отразилось на температу-
ре термостата? Ответ дать в СИ.
A R
7.11. На рисунке изображена электрическая цепь. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
В ней R1 = 1 Ом, R2 = 3 Ом, R3 = 2 Ом. Определить, во R |
|
R |
|
|
R |
|
|
|
||||||
сколько раз сопротивление между точками B и |
D |
|
|
R |
|
|
||||||||
больше, чем сопротивление между точками A и C. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
C |
||||
|
|
|
|
|
|
|
|
|
|
|||||
7.12. К одному концу двухпроводной линии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
передачи электроэнергии подсоединён источник |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
постоянного напряжения И, а к другому – нагруз- |
И |
|
|
|
|
|
|
|
|
|
Н |
|||
|
|
|
|
|
|
|
|
|||||||
ка Н с сопротивлением 40 Ом. Сопротивление |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
каждого провода линии равно 25 Ом. В линии произошло повреждение изоляции, в результате чего ток через источник возрос в 2 раза, а ток через нагрузку упал в 8 раз. Найти в СИ сопротивление изоляции в месте повреждения.
7.13.Нагреватель кипятильника состоит из четырёх одинаковых элементов. Сопротивление каждого из них 1 Ом. Нагреватель питается от батареи с э.д.с. 8
Ви внутренним сопротивлением 1 Ом. Элементы нагревателя включены так, чтобы вода нагревалась наиболее быстро. Найти в СИ мощность нагревателя.
7.14.В двухпроводной линии длиной l = 3,6 км на некотором расстоянии x
от её начала произошло частичное нарушение изоляции. Для поиска места нарушения провели следующие три измерения.
Входное сопротивление при разомкнутом выходе
– 9 Ом.
Входное сопротивление при замкнутом накоротко
x
l |
161
выходе – 6 Ом.
Выходное сопротивление при разомкнутом входе – 12 Ом. Определить в км расстояние x.
7.15.На однородный проводящий стержень падает перпендикулярно его оси пучок электронов. Пучок – стационарный и однородный, то есть каждую секунду на каждый сантиметр длины стержня попадает одно и то же количество электронов. Сопротивление стержня 0,3 Ом. Каждый его конец с помощью одинаковых проводников (шин) заземлён. Сила тока через каждую из шин 120 мА. Определить в мВ разность потенциалов между серединой стержня и его концами.
7.16.Конденсаторная батарея, состоящая из двух последовательно соединённых конденсаторов с ёмкостями С1 = 3 мкФ и С2 = 2 мкФ, подключена для зарядки к источнику питания с э.д.с. 15 В. К этому же источнику параллельно с батареей подключено активное сопротивление. В конце зарядки напряжение конденсаторах равно U1 и U2, а сила тока через источник равна I1. Если сопротивление закоротить, то через некоторое время через источник будет течь постоянный ток, равный 3I1. Определить в СИ величину U1.
162

ТЕМА 8. ЭЛЕКТРОМАГНЕТИЗМ 8.1. МАГНИТНОЕ ПОЛЕ
Магнитное поле – это силовое поле, посредством которого осуществляются магнитные взаимодействия. Источниками магнитного поля являются постоянные магниты и движущиеся электрические заряды (электрические токи). Магнитное поле проявляется в действии на магниты, движущиеся электрические заряды, проводники и рамки с электрическим током.
Индукция магнитного поля (магнитная индукция) B – это векторная физическая величина, характеризующая магнитное поле и определяющая силу, действующую на движущуюся заряженную частицу со стороны магнитного поля. Единица измерения магнитной индукции – тесла: [B] = 1 Тл.
Графически магнитное поле изображается при помощи силовых линий.
Магнитные силовые линии (линии магнитной индукции) – это кривые, каса-
тельная к которым в любой точке совпадает с направлением вектора магнитной индукции в этой точке. Силовые линии магнитного поля всегда замкнуты, что свидетельствует об отсутствии в природе магнитных зарядов.
Если силовая линия перпендикулярна плоскости чертежа, то принято использовать следующие обозначения:
 – вектор магнитной индукции B направлен от нас;
– вектор магнитной индукции B направлен от нас;
 – вектор магнитной индукции B направлен к нам.
– вектор магнитной индукции B направлен к нам.
Однородное магнитное поле – это поле, в каждой точке которого вектор магнитной индукции одинаков по величине и имеет одно направление.
Если в магнитное поле поместить вещество, то магнитная индукция при этом изменится. Вещества, в которых происходит увеличение магнитной индукции, называют ферромагнетиками (железо, кобальт, никель). Магнитная проницаемость ферромагнетика μ – это физическая величина, показывающая, во сколько раз увеличивается индукция магнитного поля в присутствии
этого вещества: |
|
B B0 , μ >> 1, |
(8.1) |
где B0 – магнитная индукция в отсутствие ферромагнетика. Для вакуума (воздуха) μ = 1.
8.2. МАГНИТНЫЕ СИЛЫ Сила Лоренца – векторная величина, определяющая силу, действующую
на заряженную частицу, движущуюся в магнитном поле. Модуль этой силы определяется выражением:
|
(8.2) |
FЛ qvBsin(vB), |
где q – заряд частицы, v – её скорость, B – индукция магнитного поля, (vB) – угол между направлением вектора скорости и вектором магнитной индукции (силовой линии). Направление силы Лоренца, действующей на положительно заряженную частицу, определяется по правилу правой руки. Правило правой руки: если расположить правую руку так, чтобы четыре пальца совпадали по направлению с вектором скорости, большой палец совпадал с направлением
163
вектора магнитной индукции, тогда сила Лоренца будет входить в ладонь. Поскольку сила Лоренца перпендикулярна плоскости, в которой лежат вектора скорости и магнитной индукции, то она не совершает работы по перемещению, а только искривляет траекторию движения заряженных частиц (сообщает центростремительное ускорение).
Сила Ампера – это сила, с которой магнитное поле действует на проводник с электрическим током. Модуль этой силы определяется формулой:
FА IlBsin(lB), |
(8.3) |
где I – сила тока в проводнике, l – длина проводника, B – индукция магнитного поля, (lB) – угол между направлением тока (вектором длины проводника) и вектором магнитной индукции (силовой линии). Вектор силы Ампера всегда перпендикулярен плоскости, в которой находятся проводник и вектор индукции магнитного поля. Направление силы Ампера определяется по правилу правой руки.
На плоский замкнутый контур с током, помещённый в магнитное поле, действует механический момент сил, оказывающий на рамку ориентирующее
воздействие. Модуль вращающего момента: |
|
M ISBsin(nB), |
(8.4) |
где I – сила тока в контуре, S – площадь, охватываемая контуром, B – индукция магнитного поля, n – нормаль к плоскости контура (вектор единичной длины перпендикулярный этой плоскости), (nB) – угол между направлением нормали
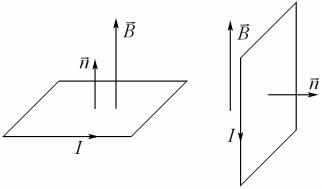
и вектором магнитной индукции. Когда векторы n и B параллельны (рис. 8.1, а), вращающий момент сил равен нулю, и контур находится в положении устойчивого равновесия. Если векторы n и B взаимно перпендикулярны (рис. 8.1, б), то на контур действует максимальный момент сил: Mmax ISB.
а) б)
Рисунок 8.1 – Контур с током в магнитном поле
8.3. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ Магнитный поток Ф (поток магнитной индукции) однородного магнит-
ного поля с индукцией B через поверхность площадью S, определяется выражением:
Ф BScos(nB). |
(8.5) |
Единица измерения магнитного потока – вебер: [Ф] = 1 Вб.
164

Магнитный поток Ψ через поперечное сечение катушки, состоящей из одинаковых витков плотно прилегающих друг к другу, называется потокосцеплением и определяется следующим образом:
NФ, |
(8.6) |
где N – число витков в катушке, Ф – поток через один из её витков.
Явление электромагнитной индукции состоит в том, что при изменении магнитного потока, пронизывающего контур, в нём возникает сторонняя электродвижущая сила (ЭДС) индукции, вызывающая появление индукционного тока. ЭДС индукции εi и сила индукционного тока Ii – скалярные величины: их знак определяется относительно заранее выбранного положительного направления обхода контура.
Закон электромагнитной индукции (закон Фарадея): ЭДС индукции,
возникающая в контуре, пропорциональна скорости изменения магнитного по-
тока, пронизывающего этот контур: |
|
|
i |
Ф t. |
(8.7) |
Здесь Ф = Ф2 – Ф1 обозначает приращение магнитного потока за время |
t, где |
|
Ф1 и Ф2 есть, соответственно, начальное и конечное значения магнитного потока. Знак минус в законе Фарадея (8.7) обусловлен соглашением о том, что положительное направление обхода контура и направление нормали к плоскости контура связаны между собой по правилу правого винта.
Согласно правилу Ленца индукционный ток имеет такое направление, при котором создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Если за время t магнитный поток изменился от значения Ф1 до значения Ф2 и закон его изменения не известен, то по формуле (8.7) можно вычислить только среднее значение ЭДС индукции. В случае равномерного изменения магнитного потока выражение (8.7) даёт точное (неизменное во времени) значение ЭДС индукции.
Согласно (8.5) простейшими причинами, вызывающими изменение магнитного потока, являются: 1) изменение магнитной индукции B по величине; 2) изменение угла между вектором магнитной индукции и нормалью к плоскости контура (вращение контура); 3) изменение площади S, охватываемой контуром. Если в постоянном магнитном поле движется прямолинейный проводник, то возникающую в нём ЭДС индукции также можно рассчитать по формуле (8.7), где под Ф нужно понимать магнитный поток через площадь, пересеченную (прочерченную) за время t проводником при его перемещении на расстояние x (рис. 8.2).
Рисунок 8.2 – Движение проводника в магнитном поле
165
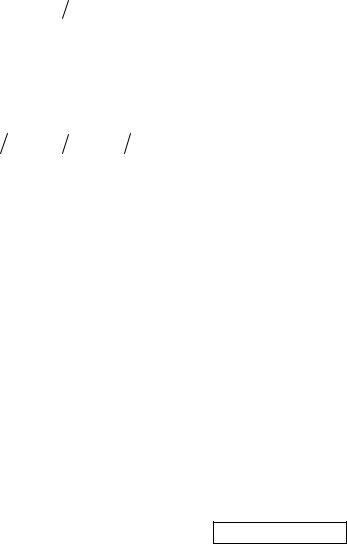
Так, для проводника длиной l, движущегося со скоростью v перпендикулярно линиям индукции B однородного магнитного поля из выражения (8.7) можно получить
i |
Blv. |
(8.8) |
Электрический ток, протекая по замкнутому контуру, создаёт магнитное поле, силовые линии которого пронизывают площадь, охватываемую этим контуром. Магнитный поток Ф сквозь этот контур пропорционален силе протекающего по нему тока I:
Ф LI, |
(8.9) |
где коэффициент пропорциональности L называется индуктивностью контура. Единица измерения индуктивности – генри: [L] = 1 Гн. Индуктивность контура (проводника) зависит от его размеров, формы и магнитных свойств среды, в которой он находится.
Явление самоиндукции – это явление возникновения ЭДС индукции в контуре при изменении силы электрического тока, текущего по этому контуру. Если индуктивность проводника неизменна (L = const), то ЭДС самоиндукции
пропорциональна скорости изменения силы электрического тока: |
|
Si L I t. |
(8.10) |
Здесь I = I2 – I1 обозначает приращение силы тока за время t, где I1 |
и I2 есть, |
соответственно, начальное и конечное значения силы тока в проводнике. |
|
В пространстве, где существует магнитное поле, распределена энергия. |
|
Энергия магнитного поля, создаваемого проводником с индуктивностью L, по |
|
которому течёт ток силой I, находится по формулам: |
|
W LI2 2 ФI 2 Ф2 2L, |
(8.11) |
L |
|
где Ф – магнитный поток сквозь замкнутый контур с током. |
|
8.4.ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1.Проволочная квадратная рамка со стороной 20 см и током 5 А помещена
воднородное магнитное поле так, что её плоскость параллельна линиям магнитной индукции. Найти величину магнитной индукции, если со стороны магнитного поля на рамку действует момент сил 0,2 Н∙м. Ответ дать в единицах СИ.
Решение:
Дано: |
|
Запишем выражение для |
механического |
момента сил M, |
||||
|
действующего на рамку |
с |
током I |
в |
магнитном поле: |
|||
a = 0,2 м |
|
|||||||
|
M = IBS∙sinα. Ориентация контура соответствует рисунку 8.1, б, |
|||||||
I = 5 А |
|
|||||||
|
откуда видно, что угол α между нормалью к контуру и векто- |
|||||||
M = 0,2 Н∙м |
|
|||||||
|
ром магнитной |
индукции |
прямой |
(sinα = 1). |
Площадь |
|||
Найти: |
|
квадратной рамки равна S = a2. Таким образом, для момента |
||||||
B = ? |
|
сил будем иметь следующее |
выражение M = IBa2. Выражая |
|||||
индукцию |
магнитного поля |
B = M/Ia2 |
и |
проводя |
расчёт, |
получим |
||
B = 0,2/(5∙0,22) = 1 Тл.
Ответ: B = 1 Тл.
166

Дано: |
Под действием |
силы |
|
|
Лоренца |
FЛ |
протон |
|
|
B = 10–4 Тл |
|
|||
R = 0,05 м |
совершает |
равномерное |
|
|
движение |
по окружности с |
|
||
q/m = 108 Кл/кг |
|
|||
Найти: |
центростремительным |
|
||
ускорением aцс = v2/R, где v |
|
|||
T = ? (мс) |
|
|||
линейная |
скорость |
частицы |
|
|
|
Рисунок 8.3 – Движение |
|||
|
||||
(см. рис. 8.3). Это движение |
возникает тогда, |
|||
когда заряженная частица влетает в магнитное |
протона в магнитном поле |
|||
поле перпендикулярно его |
силовым |
линиям. |
|
|
При этом сила Лоренца FЛ = qvBsinα становится
максимальной (sinα = 1): FЛ = qvB. Запишем второй закон Ньютона для вращающегося протона: aцс = FЛ/m. Приравнивая выражения для центростремительного ускорения, получим формулу для радиуса окружности, по которой движется протон: R = mv/qB. Период вращения это время, за которое протон, двигаясь равномерно, пройдёт полную окружность длины 2πR, т.е. T = 2πR/v. В итоге, период T = 2πmv/qBv = 2πm/qB. Проводя расчёты, получим:
T = 2∙3,14/108∙10–4 = 0,628∙10–3 с = 0,628 мс.
Ответ: T = 0,628 мс.
3. Протон движется равномерно и прямолинейно в пространстве, где существуют одновременно постоянные взаимно перпендикулярные электрическое и магнитное поля, перпендикулярно этим полям. Найти скорость протона, если напряжённость электрического поля равна 8 В/м, а индукция магнитного поля 40 мТл. Ответ дать в единицах СИ.
Решение:
Дано: |
Геометрия |
задачи |
изображена |
|
|||||
на |
рисунке |
8.4. |
На |
протон |
|
||||
E= 8 В/м |
|
||||||||
действуют две силы – сила Fэл со |
|
||||||||
B = 0,04 Тл |
|
||||||||
стороны |
электрического |
поля |
|
||||||
Найти: |
исила Лоренца FЛ |
со |
стороны |
|
|||||
v = ? |
Рисунок 8.4 – Движение |
||||||||
магнитного |
поля. |
Из |
условия |
||||||
|
|||||||||
равномерного |
и |
прямолинейного |
движения |
протона в электрическом |
|||||
протона (ускорение |
a = 0) |
по второму |
закону |
и магнитном полях |
|||||
Ньютона следует, что равнодействующая |
Fэл = FЛ. Подставляя сюда |
||||||||
приложенных |
к частице |
сил равна нулю, |
т.е. |
||||||
выражения для сил qE = qvB, приходим к выражению для искомой скорости движения протона: v = E/B. Вычислим: v =8/0,04 = 200 м/с.
Ответ: v = 200 м/с.
167
4. В вертикальном магнитном поле лежат горизонтальные рельсы на расстоянии 2 м друг от друга. Между рельсами приложено напряжение. Если на рельсы перпендикулярно им положить металлический стержень массой 0,5 кг, то по нему потечёт ток силой 50 А и он начнёт скользить по рельсам с ускорением 2 м/с2. Определить в СИ магнитную индукцию. Трением пренебречь.
Решение:
Дано: l = 2 м
m = 0,5 кг
I = 50 А a = 2 м/с2
Найти:
B = ?
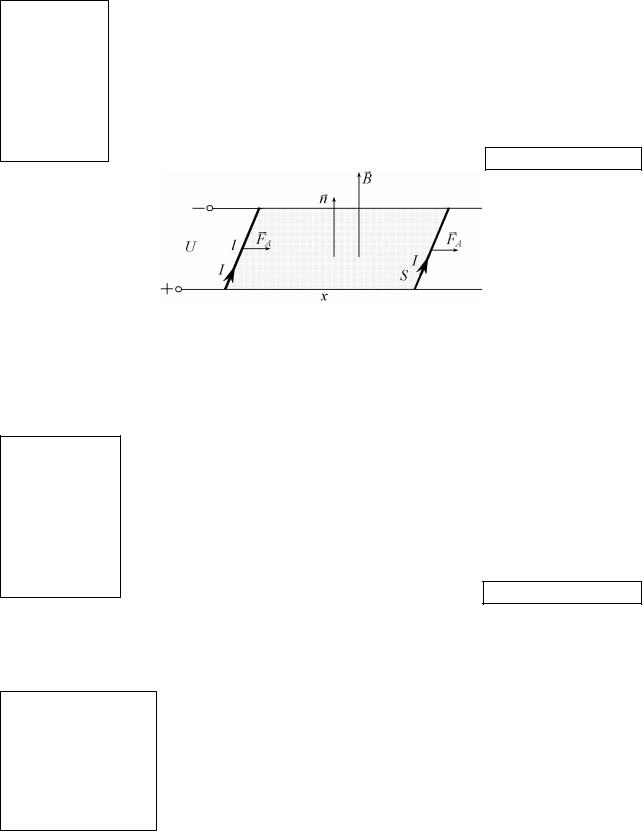
На проводник с током I со стороны магнитного поля с индукцией B (см. рис 8.5) действует сила Ампера FА = IBlsinα, которая в данном случае максимальна (sinα = 1): FА = IBl. Под действием этой силы проводник движется с ускорением (трения
не по условию) согласно второму закону |
Ньютона: |
a = FЛ/m = IBl/m. Отсюда выражаем магнитную |
индукцию |
B = am/Il. После вычислений находим B = 2∙0,5/50∙2 = 0,01 Тл.
Ответ: B = 0,01 Тл.
Рисунок 8.5 – Движение проводника с током в магнитном поле 5. Прямой проводник с током 0,2 А помещён в однородное магнитное поле с
индукцией 0,1 Тл. Длина проводника 5 см. Найти работу силы Ампера по перемещению проводника на 8 мм, если направления линий индукции, тока и перемещения взаимно перпендикулярны. Ответ дать в микроджоулях.
Решение:
Дано:
I = 0,2 А
B = 0,1 Тл
l = 0,05 м x = 8∙10–3 м
Найти:
А = ?(мкДж)
Геометрию задачи хорошо описывает рисунок 8.5 из предыдущей задачи. Направление перемещения проводника с током совпадает с направлением действия силы Ампера, действующей на него со стороны магнитного поля. При этом сила Ампера совершает над проводником механическую работу A = FA∙x = IBl∙x. Подставляя численные значения,
получим: A = 0,2∙0,1∙0,05∙8∙10–3 = 8∙10–6 Дж = 8 мкДж.
Ответ: А = 8 мкДж.
6. Определить среднее значение индукции магнитного поля внутри плоского контура площадью 30 м2 при пропускании через него тока 0,2 А. Индуктивность контура 0,3 Гн. Ответ дать в миллитеслах.
Решение:
Ток I, протекающий по контуру, создаёт в пространстве неоднородное магнитное поле. Внутри витка заменим его однородным полем с некоторым средним значением магнитной индукции Bср. Поскольку силовые линии магнитного поля, создаваемого контуром с током,
168
проходят к его плоскости перпендикулярно, выражение для магнитного потока, пронизывающего контур Ф = BсрScosα принимает вид Ф = BсрS. С другой стороны, этот магнитный поток связан с силой тока в контуре через индуктивность контура: Ф = LI. Приравнивая эти два выражения для магнитного потока и выражая магнитную индукцию, получим Bср = LI/S.
Проведём расчёты: Bср = 0,3∙0,2/30 = 2∙10–3 Тл = 2 мТл.
Ответ: Bср = 2 мТл.
7. За 2 с индукция однородного магнитного поля равномерно изменилась от 0,3 Тл до 0,1 Тл. В результате этого в круговом витке, помещённом в магнитное поле, возникла ЭДС индукции 20 мВ. Найти площадь витка, если угол между вектором магнитной индукции и нормалью к плоскости витка равен 60о. Ответ дать в единицах СИ.
Решение:
Дано: t = 2 с
B1 = 0,3 Тл B2= 0,1 Тл
ε = 0,02 В α = 60o
Найти:
S = ?

Решение:
Дано:
I1 = 2 А Ф1 = 0,5 Вб I2 = 0,5 А
εSi = 3 В
Найти: t = ?
Найти искомое время t можно из выражения для ЭДС самоиндукции: εSi = –L I/Δt, где приращение тока в катушке известно: I = I2 – I1. Неизвестную нам индуктивность, мы можем найти из выражения для магнитного потока L = Ф1/I1. Выражая искомое время через ЭДС самоиндукции и подставляя приращение тока и индуктивность, получим t = –L I/εSi = –Ф1(I2 – I1)/I1εSi = Ф1(I1 – I2)/I1εSi.
Вычисляя, получим t = 0,5∙(2 – 0,5)/2∙3 = 0,125 с.
Ответ: t = 0,125 с.
10. При уменьшении силы тока в проволочной катушке с 6 А до 4 А произошло уменьшение энергии магнитного поля на 2 Дж. Определить на сколько уменьшился магнитный поток, пронизывающий катушку. Ответ дать в единицах СИ.
Решение:
Дано: |
Запишем |
выражения |
для |
магнитного |
|
потока, |
|||
пронизывающего катушку при двух значениях протекающего |
|||||||||
I1 = 6 А |
|||||||||
по ней тока: |
Ф1 = LI1, |
Ф2 = LI2. Взяв разность этих потоков, |
|||||||
I2 = 4 А |
|||||||||
получим |
Ф = Ф1 – Ф2 = L(I1 – I2). |
Неизвестную |
нам |
||||||
WL = 2 Дж |
|||||||||
индуктивность мы можем найти из выражения для изменения |
|||||||||
Найти: |
|||||||||
энергии магнитного |
поля |
WL = WL1 – WL2= L(I12 – I22)/2, |
|||||||
Ф = ? |
L = 2ΔWL/(I12 – I22). Подставим индуктивность в |
выражение |
|||||||
|
|||||||||
для изменения магнитного потока: Ф = 2ΔWL(I1 – I2)/(I12 – I22) = 2ΔWL/(I1 + I2). |
|||||||||
Подставляя численные значения, получим Ф = 2∙2/(6 + 4) = 0,4 Вб. |
|
||||||||
|
|
|
|
|
|
Ответ: |
Ф = 0,4 Вб. |
||
8.5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задачи 3 класса трудности
3.1.В замкнутой проводящей катушке с индуктивностью 3 Гн ток равномерно изменился от 5 до 10 А за некоторый промежуток времени t. Определить
вСИ величину t, если в катушке возникает при этом э.д.с. самоиндукции 3 В.
3.2.Магнитный поток, пронизывающий поперечное сечение катушки, состоящей из 100 витков, равномерно изменился за 10 секунд от 100 Вб до 50 Вб. Определить в СИ э.д.с. индукции, возникающей в катушке.
3.3.Замкнутый контур, по которому течёт ток 2 А, находится в однородном магнитном поле. Плоскость контура параллельна линиям индукции. Со
стороны магнитного поля на контур действует момент сил 0,6 Н м. Определить
вСИ площадь контура, если величина магнитной индукции равна 1 Тл.
3.4.На проводник с током длиной 0,1 м, находящийся в однородном магнитном поле с индукцией 5 Тл, действует сила 2 Н. Ось проводника составляет
угол 30 с линиями индукции магнитного поля. Определить в СИ величину тока, протекающего по проводнику.
170
