Физика
..pdf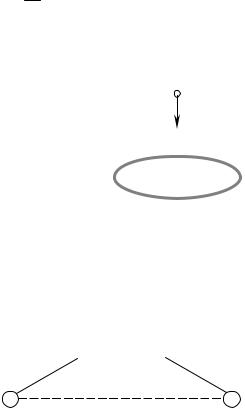
но 600 В. Определить в СИ максимальную величину э.д.с. источника напряжения,
ккоторому можно подключить эту конденсаторную батарею для её зарядки.
7.9.Обкладки плоского воздушного конденсатора ёмкостью 2 мкФ присоединены к аккумулятору, э.д.с. которого 100 В. Расстояние между обкладками 24 мм. На сколько ньютонов изменится сила притяжения между обкладками, если конденсатор, не отключая от аккумулятора, опустить в жидкость с диэлектрической проницаемостью, равной 7?
7.10.Металлический шар радиусом 10 см заряжен с поверхностной плотностью заряда 5 мкКл/м2 и помещён в среду с диэлектрической проницаемостью 30. На расстоянии 20 см от поверхности этого шара расположен положительный точечный заряд. Величина заряда 5 мкКл. На сколько миллиджоулей увеличится энергия этой системы зарядов, если точечный заряд приблизить к шару на 5 см?
7.11.Обкладки большого плоского конденсатора расположены горизонтально, а между ними на нити подвешен металлический шарик массой 1 г. Если
шарик не заряжен, то период его колебаний равен 
14 с. При сообщении шарику положительного заряда q период его колебаний уменьшился в 1,2 раза. Определить в СИ период колебаний шарика, если его заряд изменить на противоположный, то есть на –q.
7.12. Положительно заряженная капелька (q1 = 2 нКл) |
v |
|
приближается к отрицательно заряженному (q2 = –4 мкКл) |
||
|
||
тонкому металлическому кольцу радиусом 40 см. Масса ка- |
|
|
пельки 9 мг, траектория капельки совпадает с осью кольца. В |
|
|
тот момент, когда расстояние между капелькой и плоскостью |
|
|
кольца равно 30 см, её скорость равна 1 м/с. Определить в СИ |
|
|
скорость капельки в центре кольца. |
|
Задачи 8 класса трудности
8.1. Две одинаковые заряженные частицы приближаются друг к другу, и при этом их траектории лежат в одной и той же плоскости. Масса каждой частицы m = 1 г, заряд q = 10–4 Кл. В некоторый момент времени частицы находятся на расстоянии 2 м друг от друга, при этом скорость каждой из них равна 300 м/с и на- 
правлена под углом 30 к прямой, которая их соединяет. Определить в СИ, на какое минимальное расстояние сблизятся частицы.
141
ТЕМА 7. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 7.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Электрический ток – это явление направленного (упорядоченного) движения электрических зарядов. За направление тока принимают направление движения положительных зарядов.
Постоянный электрический ток – это ток, не изменяющийся с течением времени ни по силе, ни по направлению.
Сила тока I – скалярная физическая величина, равная отношению количества заряда q, переносимого через поперечное сечение проводника за интер-
вал времени t, к этому промежутку времени: |
|
I q t. |
(7.1) |
Единица измерения силы тока – ампер: [I] = 1 А.
Плотность тока j – скалярная физическая величина, равная отношению силы тока I, проходящего через проводник, к площади поперечного сечения проводника S:
j I S. |
(7.2) |
Единица измерения плотности тока: [j] = 1 А/м2.
Источник электрического тока – это устройство, поддерживающее разность потенциалов на концах электрической цепи. В замкнутой электрической цепи ток вне источника течёт от положительного полюса к отрицательному, а внутри источника – от отрицательного полюса к положительному. Движение зарядов внутри источника возможно лишь под действием так называемой сторонней силы (силы неэлектрического происхождения).
Электродвижущей силой (ЭДС) источника называется величина, равная отношению работы сторонних сил Aс1–2 при перемещении на участке электрической цепи 1–2 положительного заряда q к величине этого заряда:
|
1 2 |
AС |
q. |
(7.3) |
|
1 2 |
|
|
Напряжением (падением напряжения) U1–2 на участке цепи 1–2 называ-
ется величина, равная отношению суммарной работы кулоновских и сторонних сил при перемещении на участке 1–2 положительного заряда q к величине этого заряда:
U1 2 A1К 2 A1С 2 
q.
Так как работа кулоновских сил AК1–2 = q(φ1 – φ1), можно записать:
U1 2 |
1 2 1 2 , |
(7.4) |
Единица измерения ЭДС и напряжения – вольт [U] = 1 В.
7.2. ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ. ЗАКОН ОМА Электрическое сопротивление проводника R – физическая величина, оп-
ределяющая силу тока, текущего по нему при заданном напряжении на концах проводника. Сопротивление проводника постоянного сечения, выполненного из однородного материала, задаётся выражением:
R l S, |
(7.5) |
где ρ – удельное сопротивление материала проводника, l – длина и S – площадь поперечного сечения проводника.
142
Единица измерения электрического сопротивления – Ом: [R] = 1 Ом, а удельного сопротивления – [ρ] = 1 Ом∙м.
Зависимость удельного сопротивления от температуры описывается соотношением:
0(1 t), |
(7.6) |
где ρ0 – удельное сопротивление при 0 оС, t – температура по шкале Цельсия, α – температурный коэффициент сопротивления ([α] = 1 К–1).
Электрическое сопротивление r источника тока называется его внутрен-
ним сопротивлением.
Для произвольного участка электрической цепи 1–2, содержащего источник постоянного тока, можно записать закон Ома:
I U1 2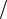 
R1 2 [ 1 2 1 2]
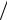R1 2 , (7.7)
где сопротивление рассматриваемого участка цепи R1–2 равно сумме внешнего и внутреннего сопротивлений: R1–2 = R + r. Рассмотрим два частных случая (7.7).
1. Участок цепи, не содержащий источника тока, называется однородным
(ε = 0, r = 0). Получаем закон Ома для однородного участка цепи:
I 1 2 R U R. |
(7.8) |
2. Замкнутая цепь, содержащая источник тока (φ1 = φ2). Получим закон Ома для замкнутой цепи:
I (R r). |
(7.9) |
Последовательное соединение проводников (рис. 7.1, а) характеризуется следующими закономерностями:
–Сила тока во всех проводниках одинакова: I1 = I2 = … = IN = I.
–Полное напряжение U на концах участка цепи равно сумме напряжений на отдельных проводниках: U = U1 + U2 + … + UN.
–Общее сопротивление R участка цепи равно сумме сопротивлений каждого из проводников:
R = R1 + R2 + … + RN. |
(7.10) |
– Напряжение на концах отдельных проводников прямо пропорционально их сопротивлениям: U1 /U2 = R1 /R2.
а) б)
Рисунок 7.1 – Соединения проводников: а) последовательное; б) параллельное
Параллельное соединение проводников (рис. 7.1, б) имеет следующие закономерности:
–Сила тока в неразветвлённой части цепи равна сумме сил токов, текущих
вкаждом проводнике: I = I1 + I2 + … + IN.
143
– Падение напряжение U на всех проводниках одинаково:
U= U1 = U2 = … = UN.
–Величина, обратная общему сопротивлению участка цепи, равна сумме
обратных величин сопротивлений каждого проводника:
1/R = 1/R1 + 1/R2 + … + 1/RN. (7.11)
– Силы токов в каждом из проводников обратно пропорциональны их сопротивлениям: I1 /I2 = R2 /R1.
7.3. РАБОТА И ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА
Работа A, которая совершается в течение времени t постоянным током силы I, текущим по участку цепи, на концах которого поддерживается напряжение U, определяется выражением:
A IUt. |
(7.12) |
Мощность, развиваемая электрическим током на этом участке цепи: |
|
P A t IU. |
(7.13) |
Теплота Q, выделяющаяся в течении времени t в проводнике сопротивлением R при прохождении по нему тока силой I, определяется законом Джоуля–
Ленца: |
|
Q I2Rt. |
(7.14) |
Мощность тепловых потерь (теплота, выделяемая в единицу времени): |
|
PQ Q t I2R. |
(7.15) |
В однородном участке цепи (ε = 0, r = 0) выделяющаяся теплота равна ра- |
|
боте электрического тока: |
|
Q I2Rt U2t R IUt A. |
(7.16) |
В неоднородном участке цепи, содержащем источник ЭДС, выделяющаяся теплота Q равна сумме работы электрического тока A и работы источника Aи:
Q A AИ , где AИ I t. |
(7.17) |
Развиваемая источником тока мощность: PИ AИ t I . |
|
Коэффициент полезного действия (КПД) η источника тока: |
|
P PИ U R (R r). |
(7.18) |
7.4.ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1.К аккумулятору с внутренним сопротивлением 2 Ом и ЭДС 12 В подключена электрическая лампочка сопротивлением 8 Ом. Определить заряд, который будет перенесён через лампочку за 5 минут. Ответ дать в единицах СИ.
Дано: r = 2 Ом ε = 12 В
R = 8 Ом t = 300 c
Найти: q = ?
Решение:
Запишем определение силы тока I = q/Δt. Отсюда заряд, который будет перенесён через лампочку за время t: q = I∙Δt. Силу тока I можно определить и закона Ома для замкнутой цепи: I = ε/(R + r). В результате для заряда получим выражение: q = ε t/(R + r). Подставляя численные значения и проводя расчеты, получим: q = 12∙300/(8 + 2) = 360 Кл.
Ответ: q = 360 Кл.
144
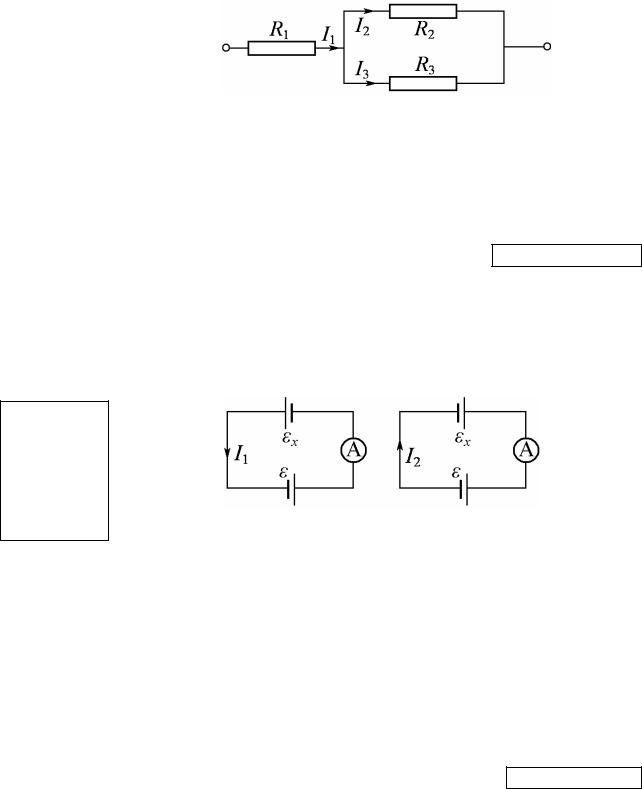
2. Нагрузкой усилителя служит цепь, состоящая из резистора R1 сопротивлением 2 Ом, включенного последовательно с параллельно соединёнными резисторами R2 = 5 Ом и R3 = 20 Ом. Ток в резисторе R2 равен 1 А. Найти силу тока в резисторе R1. Ответ дать в единицах СИ.
Решение:
Дано: |
|
|
R1 |
= 2 Ом |
|
R2 |
= 5 Ом |
|
R3 |
= 20 Ом |
Рисунок 7.2 – Разветвлённое соединение |
I2 = 1 А |
||
Найти: |
Для разветвлённой цепи, изображённой на рисунке 7.2, |
|
I1 = ? |
справедливо условие: I1 = I2 + I3. Найдём значение силы тока I3. |
|
|
|
Для этого учтём, что при параллельном соединении резисторов |
|
|
|
напряжение на них одинаково: U2 = U3, т.е. I2R2 = I3R3. Отсюда I3 = I2R2/R3. В итоге, I1 = I2 + I2R2/R3 = I2(R3 + R2)/R3. Обратим внимание на то, что значение R1 нам не понадобилось. Проводя вычисления, получим I1 = 1∙(20 + 5)/20 = 1,25 А.
Ответ: I1 = 1,25 А.
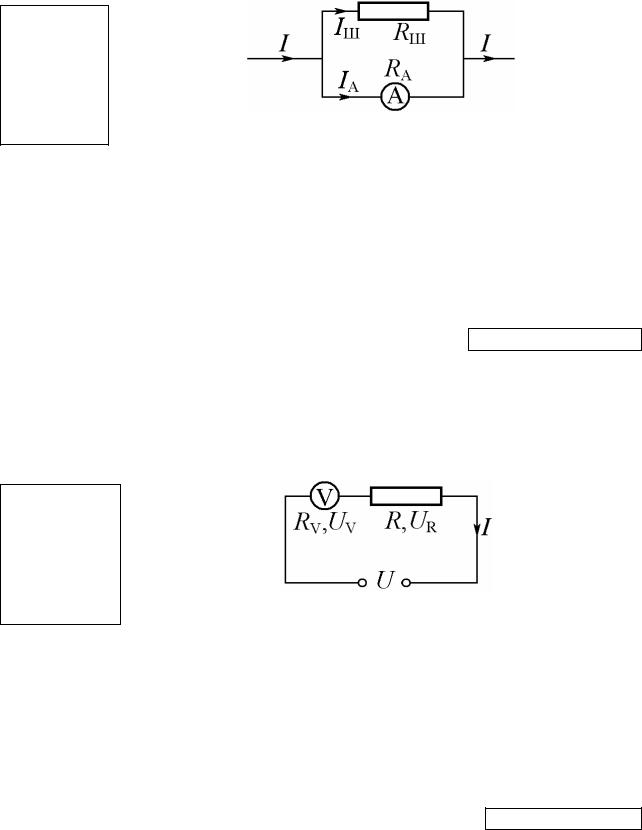
3. Для измерения ЭДС своего аккумулятора автомобилист последовательно соединил источник с ЭДС, равной 2 В, и амперметр. При этом амперметр показал ток равный 1 А. При изменении полярности включения аккумулятора ток в цепи стал равен 0,75 А. Какова ЭДС аккумулятора? Ответ дать в единицах СИ.
Решение:
Дано: |
|
|
|
ε = 2 В |
|
||
I1 |
= 1 |
А |
|
I2 |
= 0,75 А |
|
|
Найти: |
|
||
εx = ? |
а) |
б) |
|
Рисунок 7.3 – Включение источников тока в цепь: а) последовательное; б) встречное
При первом способе включения в цепь источников тока (рис. 7.3, а) их ЭДС складываются, т.е. результирующая ЭДС в цепи равна: ε1 = ε + εx. Из закона Ома для замкнутой цепи сила тока I1 = ε1/R = (ε + εx)/R, где R – полное сопротивление цепи. При втором способе соединения (рис. 7.3, б) источники тока включены навстречу друг другу, поэтому результирующая ЭДС в цепи будет находиться как ε2 = εx – ε (предполагая, что εx > ε). Используя закон Ома для данного случая, получим: I2 = ε2/R = (εx – ε)/R. Взяв отношение выражений для сил токов I1/I2 = (εx + ε)/(εx – ε) и выражая εx, получим: εx = ε∙(I1 + I2)/(I1 – I2). Вы-
числим: εx = 2∙(1 + 0,75)/(1 – 0,75) = 14 В.
Ответ: εx = 14 В.
145
6. Шнур питания магнитофона изготовлен из проводника с удельным сопротивлением 40 нОм∙м и плотностью 8000 кг/м3. Определить массу материала, пошедшего на изготовление провода, если его поперечное сечение 3 мм2 и сопротивление 0,01 Ом. Ответ дать в единицах СИ.
Решение:
Дано:
ρR = 4∙10–8 Ом∙м ρ = 8∙103 кг/м3 S = 3∙10–6 м2
R = 0,01 Ом Найти:
m = ?
Масса проводника m пропорциональна его объёму V: m = ρV = ρSl, где l – длина проводника. Сопротивление проводника можно определить из выражения R = ρR∙l/S. Отсюда выразим длину проводника и подставим в выражение для массы: m = ρS2R/ρR. Проведём расчёты и получим: m = 8∙103∙(3∙10–6)2∙0,01/4∙10–8 = 0,018 кг.
Ответ: m = 0,018 кг.
7. Проводник из материала с температурным коэффициентом сопротивления 0,003 К–1 при включении в сеть постепенно нагрелся от 0 оС до 100 оС. Во сколько раз уменьшилась мощность, потребляемая проводником при неизменном напряжении в сети?
Решение:
Дано: |
|
Запишем выражения для мощности, потребляемой |
|||||
–1 |
проводником в начале нагрева: P0 = U2/R0, и в конце нагрева: |
||||||
α = 0,003 К |
|
2 |
/R, где |
R0 и R – начальное и конечное сопротивления |
|||
t0 = 0 oC |
|
P = U |
|||||
t = 100 oC |
|
проводника. |
Тогда |
искомое отношение |
мощностей: |
||
U = const |
|
P0/P = R/R0. Подставляя сюда выражения для температурной |
|||||
|
зависимости |
сопротивления проводника (при условии |
|||||
Найти: |
|
||||||
|
неизменности |
его |
геометрических |
параметров): |
|||
P0/P = ? |
|
||||||
|
R = ρR∙l/S = ρ0∙(1 + αt)∙l/S = (ρ0l/S)∙(1 + αt) = R0∙(1 + αt), получим |
||||||
|
|
||||||
P0/P = (1 + αt). Вычисляя, находим P0/P = (1 + 0,003∙100) = 1,3. |
|
||||||
|
|
|
|
|
|
Ответ: P0/P = 1,3. |
|
8. К аккумулятору с внутренним сопротивлением 2 Ом и ЭДС 12 В подключены две последовательно соединённые лампочки сопротивлением 5 Ом каждая. Определить мощность, выделяющуюся в одной лампочке. Ответ дать в единицах СИ.
Решение:
Дано: r = 2 Ом ε = 12 В
RЛ = 5 Ом Найти:
PЛ = ?
Мощность, выделяющаяся в одной лампочке, можно рассчитать по формуле PЛ = I2RЛ. Ток I, текующий в цепи, найдём из законо Ома для замкнутой цепи: I = ε/(R + r), где R – сопротивление нагрузки, состоящей из двух последовательно соединённых ламп R = RЛ + RЛ = 2RЛ. Произведём подстановку в вуражение для мощности и получим PЛ = ε2∙RЛ/(2RЛ + r)2.
Вычислим: PЛ = 122∙5/(10 + 2)2 = 5 Вт.
Ответ: PЛ = 5 Вт.
147
Дано: |
Коэффициент |
полезного |
действия |
источника |
тока |
|||||
определяется выражением: |
η1 = R1/(R1 + r) = (1 + r/R1)–1, |
где |
||||||||
R2 |
= 2R1 |
R1 – сопротивление нагрузки, а r – внутреннее сопротивление |
||||||||
U2 |
= 1,1U1 |
|||||||||
источника. |
В итоге, нужно найти отношение r/R1. Запишем |
|||||||||
Найти: |
||||||||||
закон Ома |
для |
полной |
цепи в первом |
и втором |
случае: |
|||||
η1 |
= ? |
|||||||||
ε = I1(R1 + r) = U1 |
+ I1r, |
ε = I2(R2 + r) = U2 + I2r. |
Отсюда, |
|||||||
|
|
|||||||||
|
|
|||||||||
I1(R1 + r) = I2(R2 + r) (*). Учитывая условие задачи R2 = 2R1 и U2 = 1,1U1, найдём:
2I2R1 = 1,1∙I1R1, I2 = 0,55∙I1. |
Возвращаясь к |
выражению |
(*), получим: |
I1(R1 + r) = 0,55I1(2R1 + r), R1 + r = 1,1R1 + 0,55r, |
0,1R1 = 0,45r, |
r/R1 = 2/9. |
|
Подставляя отношение r/R1 |
в выражение для КПД, найдём: |
|
|
η1 = (1 + 2/9)–1 = 9/11 = 0,818 ≈ 82 %. |
|
|
|
Ответ: η1 = 82 %.
148
7.5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задачи 3 класса трудности
3.1. К источнику питания, э.д.с. которого 36 В, а внутреннее сопротивление 0,5 Ом, подключена электрическая лапочка. Ток в цепи 3 А. Определить в СИ сопротивление лампочки.
3.2. Сопротивление проводника при температуре 100 С составляет 13,5 Ом. Определить в СИ его сопротивление при 0 С, если температурный коэффициент сопротивления проводника 0,005 К–1.
3.3.За счет протекания тока 5 А через спираль электроплитки в ней выделяется мощность 1500 Вт. Определить в СИ сопротивление спирали.
3.4.Через проводник сопротивлением 15 Ом за 60 секунд переносится заряд 300 Кл. Определить в СИ падение напряжения на проводнике.
3.5.Электрическая цепь состоит из источника питания с внутренним сопротивлением 1 Ом и нагрузки сопротивлением 14 Ом. Ток в цепи равен 0,1 А. Определить в СИ э.д.с. источника питания.
3.6.Определить в мг массу цинка, выделившегося на катоде при пропускании через раствор сернокислого цинка постоянного тока 100 мА в течение 50 с. Электрохимический эквивалент цинка 340 мкг/Кл.
3.7.Автомобильная лампочка сопротивлением 6 Ом потребляет мощность 24 Вт. Определить в СИ ток через лампочку.
3.8.Электронный луч за 1 миллисекунду приносит на экран электроннолучевой трубки 109 электронов. Определить в мкА силу тока в электронном луче.
3.9.В спирали электроплитки плотность тока 3 кА/см2. Определить в СИ
силу тока через спираль, если площадь поперечного сечения проволоки, из которой сделана спираль, равна 0,2 мм2.
3.10.Лампочка сопротивлением 16 Ом и реостат сопротивлением 10 Ом соединены параллельно и подключены к источнику питания. Определить в СИ падение напряжения на лампочке, если потребляемый от источника питания ток равен 0,26 А.
3.11.Холодильник, включенный в сеть постоянного тока напряжением 110 В, потребляет ток 5 А. Определить в киловатт-часах количество электроэнергии, израсходованной на непрерывную работу холодильника в течение 10часов.
3.12.Две электрических лампочки, сопротивлением по 46 Ом каждая, соединены параллельно и подключены к источнику питания с внутренним сопротивлением 1 Ом. Определить в СИ э.д.с. источника питания, если ток через него равен 1 А.
3.13.Паяльник включен в сеть с напряжением 36 В. Определить в СИ количество электричества, которое должно пройти по спирали паяльника, чтобы работа тока в спирали была равной 360 Дж.
3.14.Определить в СИ сопротивление катушки громкоговорителя, если при силе тока 2 А в катушке выделяется мощность 32 Вт.
3.15.Лампочка при включении в сеть с напряжением 50 В потребляет мощность 100 Вт. Определить в СИ силу тока, протекающего по спирали лампочки.
149
3.16.За сколько секунд спираль электрического чайника выделит 2500 Дж теплоты, если по ней протекает ток силой 5 А? Сопротивление спирали 10 Ом.
3.17.Определить в СИ сопротивление спирали, если на её изготовление израсходовано 150 м нихромовой проволоки с поперечным сечением 0,2 мм2.
Удельное сопротивление нихрома 1 мкОм м.
3.18.Нагрузкой полупроводникового усилителя служит резистор сопротивлением 500 Ом. Определить в СИ количество теплоты, которое выделится в резисторе за 20 секунд при протекании в нём тока силой 100 мА.
3.19.Нагреватель термостата имеет две спирали сопротивлением 60 Ом и 40 Ом, соединённые последовательно. Определить в СИ мощность нагревателя, если через него протекает ток 2 А.
3.20.Электрическая плитка имеет две спирали сопротивлением 100 Ом каждая. Определить в СИ мощность плитки при параллельном соединении спиралей и включении её в сеть напряжением 220 В.
3.21.Определить в СИ массу меди, выделившейся при электролизе за
1000 с, если ток электролиза равен 100 А. Электрохимический эквивалент меди
3,3 10–7 кг/Кл.
3.22.Два резистора сопротивлением 20 Ом и 30 Ом включены в схему последовательно. Определить в СИ силу тока в первом резисторе, если напряжение на втором 60 В.
3.23.Два резистора сопротивлением 40 Ом и 60 Ом включены в схему параллельно. Определить в СИ силу тока в первом резисторе, если напряжение на втором 100 В.
3.24.Во сколько раз увеличится сопротивление проводника, если его нагреть на 200 К? Температурный коэффициент сопротивления 0,005 К–1.
3.25.Через поперечное сечение резистора сопротивлением 17 Ом за каждые 5 секунд переносится заряд 10 Кл. Определить в СИ мощность, выделяющуюся в резисторе.
3.26.Температурный коэффициент сопротивления проволоки в единицах
СИ равен 0,01. Сопротивление проволоки при температуре 100 С равно 100 Ом. Определить в СИ сопротивление проволоки при температуре 0 С.
3.27.В карманном фонаре лампочка сопротивлением 43 Ом потребляет ток 0,1 А. Э.д.с. батарейки 4,5 В. Определить в СИ внутреннее сопротивление батарейки.
3.28.К источнику питания, внутреннее сопротивление которого 2 Ом, подключена лампочка сопротивлением 8 Ом. Сила тока в лампочке равна 2 А. Определить в СИ э.д.с. источника питания.
3.29.Электрокипятильник потребляет мощность 1000 Вт от сети постоянного тока напряжением 110 В. Определить в СИ сопротивление кипятильника. Ответ дать в СИ.
3.30.Через раствор медного купороса, налитый в электролитическую ванну, пропускают ток 10 А в течение 2 часов. Определить в граммах массу меди,
выделившейся на катоде. Электрохимический эквивалент меди 3 10–7 кг/Кл.
150