
Статистические методы обработки сигналов в радиотехнических системах
..pdf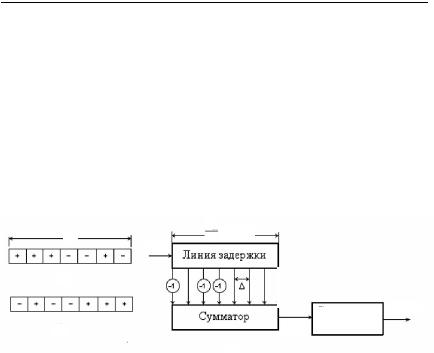
81
ной ФЧХ в полосе пропускания. Полосовой фильтр близок к СФ, если егополоса Fпр 1,37 / и . Проигрышвотношениисигнал/шумпомощности для такогофильтра составляетоколо 1,2 раза.
3.3.2.Согласованный фильтр для прямоугольного радиоимпульса с ФКМ
Определим структурную схему СФ для ФКМ-импульса с семипозиционным кодом Баркера (рис. 1.15,а). На рис 3.3,а показано условное обозначение этого сигнала. Используя выражение (3.15), получим импульсную реакцию СФ (рис. 3.3,б).
и |
|
|
и |
(n–1) |
|
|
|
||
s(t) |
|
n |
|
|
|
||||
|
Линия задержки |
|
|
|
|
||||
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласован- |
sвых(t) |
б |
|
|
Сумматор |
|
|
||||
|
|
|
s (t) |
ный фильтр |
|
||||
|
|
|
|
|
|
|
|||
в
Рис. 3.3. Обработка ФКМ-радиоимпульса в согласованном фильтре:
а — модулирующая функция ФКМ-сигнала; б — модулирующая функция импульсной реакции СФ; в — СФ для радиоимпульса с ФКМ
Устройствооптимальной обработки ФКМ сигнала (рис. 3.3,в) состоитизширокополосной линиизадержкиссемьюравноотстоящимиотводами (с интервалом задержки ), общего сумматора, к которому часть отводов подключена через инверсные каскады, а остальные — непосредственно, и линейного фильтра, согласованного с парциальным радиоимпульсомдлительностью и / 7.
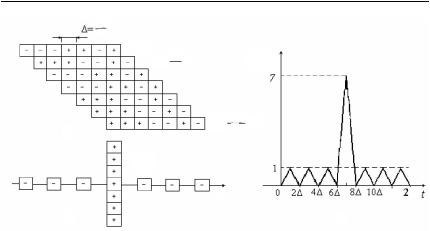
РаботуСФпоясняетрис. 3.4, накоторомпоказаныэтапыформирования радиоимпульса sвых (t) . На рис. 3.4,а с учетом инверсных каскадов схематически показаны радиоимпульсы с ФКМ на входе сумматора. Результат их суммирования представлен на рис. 3.4,б, а огибающая выходного сигнала СФ — на рис. 3.4,в. Максимум сигнала sвых (t) равен 7E1, где E1 — энергияпарциальногоимпульса.
82
и n
–s(t) |
и |
|
Sвых(t) |
s(t– |
n ) |
|
|
а |
s(t– |
n–1 |
и) |
n |
|||
s (t) |
|
|
|
|
t |
|
и |
б |
|
|
в |
Рис. 3.4. Формирование сигнала на выходе СФ: а — копии ФКМ-импульса на выходах линии задержки; б — ФКМ-сигнал на выходе сумматора;
в— огибающая ФКМ-радиосигнала на выходе СФ
3.3.3.Согласованный фильтр для пачки М когерентных радиоимпульсов гауссовской формы
Представимвходной сигнал, состоящий из М периодически следующих когерентных радиоимпульсов (рис. 3.5,а) в виде
M 1 |
|
|
s(t) s1(t nT ), |
0 t MT , |
(3.24) |
n 0
где s1(t) — одиночный радиоимпульс заданной формы с энергией E1 и длительностью и; T — периодследованияимпульсов. Спектрсигнала (3.24) равен
MT
g( )
0
M 1
n 0
M 1 |
(n 1)T |
|
s(t) e i t dt |
s1(t nT )e i t dt |
|
n 0 |
nT |
|
T |
M 1 |
|
s1(x)e i (x nT ) dx g1( ) e i nT , |
(3.25) |
|
0 |
n 0 |
|
где g1( ) s1(t) — спектр одиночного импульса. Подставим в (3.10) общуюдлительностьпачки t0 и (M 1)T ис учетомспектра пачки (3.25) найдемкоэффициентпередачиоптимальногофильтраввиде
k |
( ) ck |
( ) k |
( ); |
(3.26) |
opt |
1 |
2 |
|
|

83
|
( ) g |
|
( ) e |
i и |
; |
|
|
|||
k |
|
|
|
|
|
|||||
1 |
|
1 |
|
|
|
|
|
|
|
|
M 1 |
i mT |
|
|
1 exp( i MT ) |
|
(3.27) |
||||
k2 ( ) e |
|
|
. |
|||||||
|
|
1 exp( i T ) |
|
|||||||
m 0 |
|
|
k |
|
|
|||||
Первый сомножитель в (3.26) |
|
( ) |
естькоэффициентпередачи СФ |
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
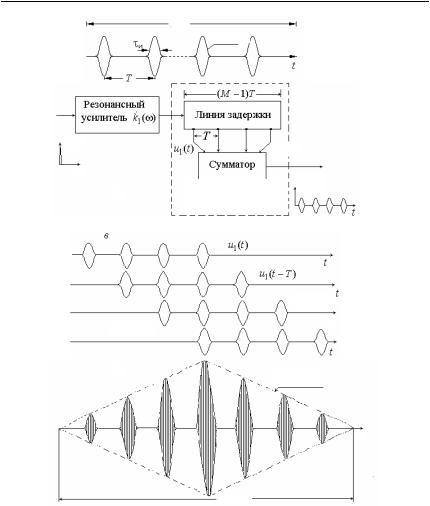
для одиночного радиоимпульса. Каждое слагаемое второго сомножителясоответствуеткоэффициентупередачизвена, обеспечивающегозадержкусигналанавремя mT. Применениеформулысуммыконечногочислаэлементовгеометрическойпрогрессиидаетвыражение(3.27). Видно, что, k2 ( ) естькоэффициентпередачимногоотводнойлиниизадержки с суммированием задержанных сигналов. Общее время задержки в линии — (M 1)T . Структурнаясхема СФдляпачки радиоимпульсов, соответствующая формуле (3.26), приведена на рис. 3.5,б. При подаче на вход СФ -импульса на выходе сумматора получается последовательность М (по числу отводов) радиоимпульсов, каждый из которых по форме повторяет импульсную реакцию фильтра, согласованного с одиночным импульсом пачки. На рис. 3.5,в условнопоказан процесс оптимальнойфильтрациипачкииз М 4 импульсовссимметричнойогибающейгауссовскойформы. Огибающаяпачкирадиоимпульсовнавыходе сумматора Sвыхopt (t) имееттреугольнуюформу, длительностьпонулям 2МТ и число импульсов 2М – 1.
Рассмотрим частотную интерпретацию работы СФ пачки. Определив из (3.27) модуль k2 ( ) , найдем АЧХ второго звена СФ в виде
K2 |
( f ) |
sin( f MT ) |
|
. |
(3.28) |
|
sin( f T ) |
||||||
|
|
|
|
|||
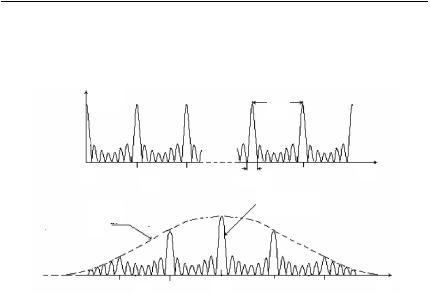
Частотная характеристика (3.28) является гребенчатой (рис. 3.6,а) с периодически повторяющимися через интервал 1/Т зубцами, ширина которыхпонулям2/(МТ). ВслучаеидеальнойлиниизадержкиАЧХ(3.28) существуетнавсейосичастот. РезультирующаяАЧХ K(f) K1( f ) K2 ( f ) практически ограничена поспектруколокольной (гауссовской) характеристикой K1( f ) фильтра, согласованногосодиночным импульсомпачки. Очевидно, чтоотношениесигнал/шумпомощностивмоментмаксимума сигнала на выходе СФ равно
2EsM |
|
2Eпачки |
, |
(3.29) |
N0 |
|
|||
|
N0 |
|
||
чтосоответствуетрезультатам подразд. 3.2.
84
МТ
|
|
|
|
|
|
|
|
S1 (t kT ) |
||||
|
|
|
|
и |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aа |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
(М–1)Т |
|
|
|
|
Резонансный |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
Линия задержки |
|
|
||||||||
|
|
k ( ) |
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
(t)
t
б
|
|
Т |
|
|
|
|
|
|
|
|
|
|
|
u1(t) |
|
|
|
|
uM (t) |
|
|
|
|
Сумматор |
|
|
|
|
|
|
|
|
|
hopt (t) |
|
|
|
|
M 1 |
|
|
k2 ( ) e i mT
|
|
m 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u1( |
t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||||
|
|
|
|
u1(t T |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u1(t 2T ) |
|
|
|
|||
t
u1(t 3T )
 t
t
в
Sвыхopt (t)
t
2МТ
г
Рис. 3.5. Согласованная фильтрация пачки когерентных радиоимпульсов гауссовской формы: а — пачка импульсов; б — структура СФ для пачки; в — последовательности импульсов на выходах линии задержки
и сумматора (M 4); г — радиоимпульсы на выходе сумматора
Напомним, чтовыигрышвотношениисигнал/шумполучаетсязасчет синфазногосуммированияимпульсныхколебанийсигналавопределенныймоментвремени. Спектральныесоставляющиешумасуммируются со случайными фазами. Гребенчатая структура АЧХ СФ, совпадаю-
85
щая со структурой амплитудно-частотного спектра когерентной пачки импульсов, обеспечивает прохождение через СФ только части спектральныхсоставляющихпомехи. НаименьшееусилениеСФимеет на техучасткахспектра, где уровеньсигнальныхсоставляющихмал.
K2( f) |
1/T |
|
|
|
|
|
|
а |
0 |
2/MT |
f |
|
|
|
K1( f) |
K1( f) K2( f) |
|
|
|
|
|
|
б |
f0 |
|
f |
Рис. 3.6. Гребенчатая АЧХ схемы оптимального суммирования (а) и результирующая АЧХ (б) согласованного фильтра
для когерентной пачки радиоимпульса
3.4.Обнаружение и различение сигналов при наличии помех (байесовский метод)
Статистическаятеорияпринятиярешенийприналичиипомехвклю-
чаетдваосновныхраздела: статистическуютеориюпроверкигипотез и статистическую теорию оценок неизвестных параметров. Для ре-
шения задач оптимального обнаружения, различения и классификации сигналов применяют аппарат статистической теории проверки гипотез. В 30-хгодах XX века американский математикДжон Нейман и английскийматематикКарлПирсон заложили основы теориипроверкигипотез.
Рассмотримдвенаиболеепростыезадачи, связанныесбинарнымразличениеми обнаружениемсигналов. В этомслучаевприемникереализуется алгоритм принятия решения в пользу одной из двух возможных гипотез: H0 или H1 . В цифровых РСПИ эти гипотезы соответствуют передаче по каналу связи на интервале [0;Т] одного из двух полезных сигналов s0(t, 0) или s1(t, 1). В РЛ- и РН-системах при решении задачи обнаружения гипотеза H0 означает отсутствие полезного сигнала, то есть s0(t, ) 0. Таким образом, задача различения является более

86
общей. Рассмотримэтузадачуиприменимдляеерешениябайесовский метод [13], основоположником которого является американский математикА. Вальд.
Постановказадачи. Наблюдаемыйсигналнавходеприемникапредставимв виде
y(t) F s1(t, 1);n(t) (1 ) F s0 (t, 0 );n(t) ; |
t 0,T , (3.30) |
где — случайная величина со значениями 0 и 1; |
F si (t, i );n(t) — |
оператор, определяющийспособвзаимодействияполезногосигнала s( ) и помехи n(t).
Априорные вероятности значений случайной величины известны: Р( 0) p0 и Р( 1) p1 . Статистические свойства помехи и сигналов предполагаются также заданными. Таким образом, при дискретном отборе данных на интервале [0,T] могут быть определены n-мер- ные условные ПРВ (см. подразд. 1.4)
W (y , y , , y |
n |
/ H |
|
) W (y / H |
), |
(3.31) |
1 2 |
|
0 |
0 |
|
||
W (y1, y2 , , yn / H1) W (y / H1), |
|
|||||
где H0 и H1 — двеслучайныегипотезы (события), соответствующие двумвозможнымсостояниямнаблюдаемогосигнала. Оптимальныйразличительнаосновеобработкисигнала y(t) долженлучшимспособомпри- нять решение о том, какая из двух гипотез реализовалась в конкретном наблюдении. Фактические данные наблюдений в статистике называют выборкой; в нашем случае это n-мерный вектор y y1, y2 ,..., yn , где
yi y(ti ) , i 1,…,n.
Решениезадачи. Очевидно, системаразличенияиз-завлиянияпомех может случайно «попасть» воднуизчетырехситуаций.
1. Состояние на входе — верна гипотеза Н1. Состояние на выходе
(решение) — верна гипотеза .
H1
2. Состояние на входе — верна гипотеза Н1. Состояние на выходе
(решение) — верна гипотеза .
H 2
3. Состояние на входе — верна гипотеза H2 . Состояние на выходе
(решение) — верна гипотеза .
H 2
4. Состояние на входе — верна гипотеза H2 . Состояние на выходе
(решение) — верна гипотеза H1 .
Видно, что ситуации 1 и 3 соответствуют правильному различению сигналов, а 2 и 4 — ошибочному.
87
Дляопределенияколичественногокритерияэффективностиразли-
чения назначим плату за результат работы системы. Очевидно, плата зависит от состояния на входе и выходе и определяется потерями, которыенесетлицо, использующеерезультатыразличениясигналов. Введем платежную матрицу C Cij , где i, j 0,1; первый индекс определяетпринятуюгипотезунавыходе(решение), второй— гипотезунавходе. Без потери общности рассуждений будем полагать плату за ошибки по-
ложительной, то есть C10 , C01> 0 , а за верные решения C00 , C11 0 . Элементы Cij записанывтаблицу.
|
Вход |
Критерий оптимальности различителя. |
|||||
Выход |
Вкачествекритерияиспользуемвеличинусред- |
||||||
H0 |
H1 |
ней платы, те. . еематематическоеожиданиепо- |
|||||
H0 |
C00 |
C01 |
терь. Втеории принятиярешений этувеличину |
||||
называютсреднимрискомR. Поправилувычис- |
|||||||
H1 |
C10 |
C11 |
ления среднего дискретной случайной величи- |
||||
|
|
|
ны Сполучим |
|
|
||
|
|
|
|
|
|
|
|
|
|
R M C C00P(H0 H 0 ) C11P(H1 H1) |
|
||||
|
|
|
|
|
|
|
(3.32) |
|
|
C01P(H1 H 0 ) C10P(H0 |
H1), |
||||
где P Hi |
|
P(Hi ) |
|
Hi |
— вероятность совместного появ- |
||
H j |
P H j |
||||||
|
|
|
|
Hi |
— условнаявероятностьпринятия |
||
лениясобытий Hi и H j ; P H j |
|||||||
|
|
в предположении, что на входе верна гипотеза Hi . |
|
||||
решения H j |
|
||||||
Для наглядности дальнейших рассуждений используем геометриче-
скую интерпретацию задачи. На |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
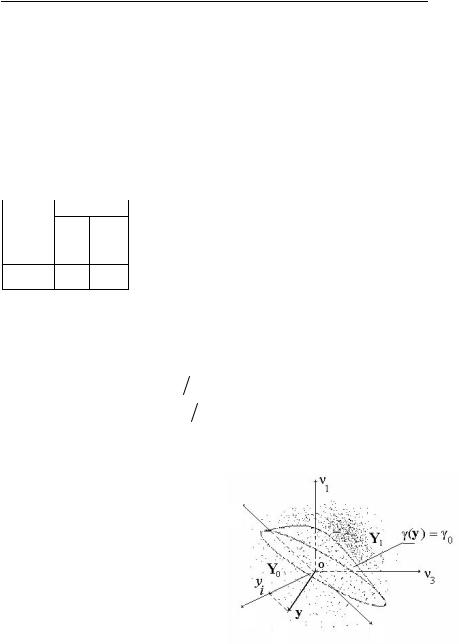
рис. 3.7 условнопоказаноn-мерное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
евклидово пространство с осями |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
координат o i (i 1 n) . Множе- |
|
|
|
|
|
|
|
|
|
|
|
|
y) |
||
|
|
|
|
|
|
|
|
|
|
Y1 |
|||||
ство возможных выборочных зна- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
чений y обозначим Y (иногда его |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
называютпространствомнаблюде- |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
y |
i |
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||||
ний). Любому выборочному векто- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ру y Y соответствует точка с ко- |
|
i |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
y |
|
|
n |
|||||||||
ординатами (у1,у2,…,уi…,уn). Одна |
|
|
Y Y Y |
|
|||||||||||
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
||
из них (yi) показана на рисунке.

88
Очевидно, чторешающееправиловбинарномслучаесводитсяктому, чтобынайтиспособразбиениямножестваY насуммудвухнепересекаю-
щихся подмножеств Y0 |
и Y1, тоесть Y Y0 |
Y1 |
. И далее, если y Y0 , |
|
|
|
|
|
|
топринимаетсярешение H 0 |
; если y Y1 , топринимаетсярешение H 1 . |
|||
Конкретное разбиение в n-мерном пространстве определено заданием уравнения поверхности, которое, в общем случае, имеет вид
( y1, y2 ,..., yn ) 0 , где 0 const. Таким образом, для всех y Y0 выполняется неравенство (y) < 0 и для y Y1 соответственно(y) > 0. Задачасостоитвтом, чтобынайтиоптимальноерешающееправило: функцию opt (y) и еепороговоезначение— величину 0. Заметим, что любое преобразование наблюдаемых данных в статистическихзадачахназываютстатистикой.
Важно отметить, что статистика opt (y) осуществляет редукцию исходных данных: на входе наблюдатель располагает n-мерным вектором y, которыйсодержитинформациюопереданномсигнале; навыходепослеобработкиполученаскалярнаявеличина . Очевидно, чтопри такомвзаимнонеоднозначномпреобразовании первичнаяинформация, в общем случае, может быть частично утрачена. Удивительно, однако, то, чтосуществуют такие статистики (их называют достаточными),
которые, несмотря на редукцию первичных данных, не ведут к потере полезной информации, содержащейся в них. Интуитивно понятно, что оптимальноерешающееправилодолжнообладатьэтимзамечательным свойством.
Оптимальноерешающееправилонайдемизусловияминимума сред- негориска (МСР) (3.32). Запишемвыражениядля условныхвероятностей в виде интегралов от соответствующих n-мерных условных ПРВ пообласти Y0:
|
/ H0 ) ... W ( y1,..., yn / H0 ) dy1 dy2...dyn; |
|
|
P(H 0 |
|
|
|
|
Y0 |
|
|
|
|
|
|
|
|
|
|
/ H0 ) 1 ... W ( y1,..., yn / H0 ) dy1 dy2...dyn |
; |
|
|
P(H1 |
|
||
|
Y0 |
|
|
|
|
(3.33) |
|
/ H1) ... W (y1,..., yn / H1) dy1 dy2...dyn ; |
|
||
P(H 0 |
|
|
|
|
Y0 |
|
|
|
|
|
|
P(H1 |
/ H1) 1 ... W (y1,..., yn / H1) dy1 dy2...dyn. |
|
|
|
Y |
|
|
|
0 |
|
|

89
Подставив выражения (3.33) в формулу (3.32), после группирования слагаемых с учетом того, что Р(Н0) р0 и Р(Н1) р1, получим
R p0C10 p1C11
... p1(C01 C11)W (y / H1) p0 (C10 C00 )W (y / H0 ) dy. (3.34)
Y0
Первые два слагаемых в (3.34) постоянны и от выборки y не зависят. Подынтегральное выражение при любых y есть разность положительных величин, поскольку C01 C11 , C10 C00 и условные функции ПРВ W (y / Hi ) 0 . Таким образом, минимум среднего риска (3.34) можнообеспечить, если для всех y Y0 выполняется условие
p1(C01 C11)W (y / H1) p0 (C10 C00 )W (y / H0 ) 0. |
(3.35) |
Преобразуя неравенство (3.35) так, чтобы в правой части оказались
постоянныевеличины, получимправилопринятиярешения
H 0
opt |
(y) |
W (y / H1) |
|
p0 (C10 |
C00 ) |
. |
(3.36) |
|
|
|
|||||
|
W (y / H0 ) |
p1(C01 C11) |
|
||||
Такимобразом, оптимальныйразличительдвухсигналовобрабатывает наблюдаемыйсигнал y иформируетнавыходерешение
, если
H1
, если
H 0
гдеоптимальныйпорог
|
|
W (y / H ) |
|
|
|
|
|||||
opt |
(y) |
|
|
1 |
|
|
0; |
|
|
||
W (y / H0 ) |
|
||||||||||
|
|
|
|
|
(3.37) |
||||||
|
|
|
W (y / H1) |
|
|
|
|||||
opt (y) |
0 |
|
|
|
|||||||
|
|
|
, |
|
|||||||
W (y / H |
0 |
) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0opt p0 (C10 |
C00 )/p1(C01 C11). |
|
|||||||||
Смысл отношения условных ПРВ в (3.37) состоит в том, что оно пропорционально отношению соответствующих вероятностей. Вычислив его для конкретной выборки y, различитель «может судить» о том, какая из двухгипотез более правдоподобна. Поэтой причине функциюopt (y) в специальной литературе называют отношением правдоподо- бия и обозначают, как правило, L(y), что связано с английским словом likеlihood — правдоподобие.
Структураустройства, котороереализуетоптимальныйалгоритмразличениясигналов, определяетсяконкретнымвидомусловныхПРВ.

90
3.5.Другие критерии оптимальности обнаружения и различения
Можно предположить, что при изменении критерия оптимальности правило принятия оптимального решения, то есть способ обработки входногосигнала, можетбытьдругим. Вовсякомслучае, повседневный опытэтоподтверждает. Например, откритерияоценкиработысотрудника зависитстратегияегоповедения. Покажем, чтобайесовкритерий(МСР) является вполне общим, те. . к нему сводятся другие не менее целесообразные критерии. Предварительно представим (3.32) для величины R в виде
|
|
|
|
R C00 p0 P(H |
0 / H0 ) C11 p1 P(H1 / H1) |
|
|
|
|
/ H0 ). |
(3.38) |
C01 p1 P(H 0 |
/ H1) C10 p0 P(H1 |
||
Критерий минимума взвешенной вероятности ошибки. Выше отмечалось, что в бинарной задаче проверки гипотез возможны четыре исхода, из которых два ошибочных и два верных. В теории проверки гипотез ошибкой 1-го рода называют случайное событие, состоящее
в том, что система принимает решение |
|
|
в пользу гипотезы H |
|
в то |
H |
1 |
1 |
|||
|
|
|
|
||
время как верна гипотеза H0 . Вероятность этой ошибки P(H1 |
/ H0 ) . |
||||
Ошибка 2-го рода состоит в появлении события при условии, что
H 0
вернагипотеза H1 . Вероятностьэтойошибки P(H 0 / H1) . Очевидно, что вполнеразумнойявляетсястратегияминимизациивзвешеннойвероятностиошибочныхрешений. Критерий, очевидно, определяетсявеличиной
|
H0 |
|
H1 , |
(3.39) |
Kош k1P H1 |
k2 P H 0 |
где k1 и k2 — весовые коэффициенты, зависящие от потерь, которые возникают вследствие допущенных ошибок. Сравнивая (3.38)
и (3.39), видим чтовеличина Kош R , если С11 С00 0; k1 p0 C10 ; k2 p1 C01 . Следовательно, данныйкритерийестьчастныйслучайкрите-
рияМСР.
Критерий идеального наблюдателя. Критерий состоит в том, что в системе принятия решений необходимо обеспечить минимум полной вероятности ошибочных ситуаций. В соответствии с формулой полной вероятностиимеем
