Статистические методы обработки сигналов в радиотехнических системах

72

гауссовcкогошума n(t), двухсторонняяспектральнаяплотностькоторого Gn ( ) N0 / 2 [Вт/Гц] для ( , ). Введем следующие обозначения: k( ) K( )ei ( ) — комплексныйкоэффициентпередачифильтра (K( ) — амплитудно-частотнаяхарактеристика(АЧХ) фильтра); ( ) — фазочастотнаяхарактеристика(ФЧХ) фильтра; g( ) g( )ei ( ) — комплексный частотный спектр полезного сигнала (g( ) — амплитудночастотныйспектр); ( ) — фазо-частотныйспектр. ВременныеиспектральныефункциисвязанывзаимнымипреобразованиямиФурье

где h( ) — импульснаяреакцияфильтра; символ обозначаетпрямое

F

иобратноеФурье-преобразованиемеждуфункциями. Полезный сигнал

Средняямощностьшуманавыходефильтраначастоте f вполосе df

кмощности шума на выходефильтра вмомент t0:

74

Оптимальный фильтр, имеющий такие характеристики, называют

согласованным линейным фильтром.

СовпадениеформыАЧХфильтра самплитудно-частотнымспектром сигнала обеспечивает наилучшее выделение тех участков спектра сигнала, на которыхотношениеуровней сигнала кшумувыше. Формасиг-

нала на выходе фильтра при этом искажается. Однако это не имеет значения, поскольку критерий оптимальности состоит не в точном воспроизведенииформысигнала, авформированиинаибольшегопикавыходногосигналанафонешума. ВажнуюрольвсвязисэтимиграетФЧХ фильтра opt ( ) . Пояснимеероль.

Подставим в (3.4) коэффициент передачи (3.10) и запишем выражениесигналана выходесогласованногофильтра (СФ)

Второеуравнениев(3.12) получаетсяизпервого, таккак g( ) 2 есть коэффициент передачи фильтра по мощности, то есть это четная функцияаргумента , поэтомувпреобразованииФурьеостаетсятолькодействительная часть. Из (3.12) следует, что форма сигнала на выходе СФ является четной функцией аргумента (t – t0 ), зависит от амплитуд- но-частотного спектра входного сигнала и не зависит от его фазо- частотного спектра.

Эта любопытная ситуация объясняется тем, что взаимные фазовые сдвиги спектральных составляющих входного сигнала, определяемые функцией ( ) компенсируются ФЧХ СФ. Поэтому все гармоническиесоставляющиевыходногосигнала вмоментвремени t t0 одновременно достигают амплитудных значений и, суммируясь, поскольку фильтрлинейный, даютпиквыходногосигнала, равныйсогласно(3.12)

Если бы ФЧХ фильтра не компенсировала фазовых сдвигов спектральныхсоставляющихвходногосигнала, томаксимумыразличныхгар-

76

y(t) s(t, 0 ) n(t ), 0 t T . (3.16)

где 0 — значение информативного параметра в полезном сигнале на входефильтра. В общемслучае 0 не являетсявременной задержкой.

Допустим, что импульсная характеристика СФ согласована с полезнымсигналомсточностьюдоинформативногопараметра, те. . егозначениедляфункции hopt (t) отличноот 0 иравно .

Напряжение на выходе СФ сучетом (3.15), (3.16) представим в виде

Сравнение выражение (1.15а) для АКФ сигнала с (3.17) и (3.18) по-

зволяет сделать важный вывод. Выходной сигнал СФ с точностью до константыссоответствуетвзаимнойкорреляционнойфункциимежду принятым колебанием y(t) и полезным сигналом s(t, ). Сигнальная

же функция zs (t, ) с точностью до константы совпадает при усло-

вии 0 с автокорреляционной функцией полезного сигнала.

Максимальное значение сигнальная функция имеет в точке t t0,

0 . В соответствии с (3.18) оно равно

является временным положением сигнала, выражение для сигнальной функцииимеетвид

77

0

где 0 и ф — соответственно временной сдвиг входного сигнала и значение сдвига, на который «настроен» СФ. Определим момент времени, когда выражение (3.20) имеет максимум. Поскольку функция zs (t; 0 , ф) k(t), то есть пропорциональна АКФ сигнала, то положение максимума совпадает с моментом времени, при котором разностьаргументов удвухкопий сигналов в (3.20) равна нулю. Видно, что разность аргументов равна t0 ( 0 ф) t и обращается в ноль, когда t t0 ( 0 ф) . Таким образом, положение максимума просто сдвинется вовремени, величина же егоостанетсянеизменной и равной (3.19). Отметим, что если бы параметр имел смысл частотного сдвига или какой-либо другой, то уровень максимума сигнала на выходе СФ оказался бы зависящим от разности ( 0 ф ).

ПосколькуформасигналанавыходеСФповторяетАКФ k( ), топри подаче на его вход прямоугольного радиоимпульса выходной сигнал соответствует сигналу на рис. 1.10. При подаче на вход радиоимпульса с ЛЧМ и гауссовской огибающей сигнал на выходе СФ «теряет» ЧМ и сжимается в B раз (см. рис. 1.13). Огибающая сигнала на выходе СФ, которая можетбыть выделена с помощью линейногодетектора, очевидно, повторяетфункцию K( ), т.е. имееттреугольнуюформудляпрямоугольногорадиоимпульса (см. рис. 1.9) и сжатую в В раз по длительности гауссоиду для гауссовcкого ЛЧМ-радиоимпульса (см. рис. 1.13).

Определим дисперсию (мощность) шума на выходе СФ. Из (3.18)

N0

4

N02 s(t0 t, ) s(t0 1 t, )Kn ( 1 )d d 1.

ПодставляявнегоАКФбелогошума (1.46) и выполняяинтегрирование с учетом свойств -функции, получим

78

Длязадачвинженернойпрактикеважнознатьотношениемаксимального значения сигнала к среднеквадратическому значению шума. Это отношение на выходе СФ определим, используя (3.19) и (3.21). В итоге получим

Как и следовало ожидать, полученный результат совпадает с (3.11)

для qmax (t0 ) .

Обсудим вопрос о том, какое значение может принимать момент отсчета t0. Если сигнал s(t), на который «настроен» СФ, возникает вмоментвремени 0 изаканчиваетсяпри t 0 и (нарис. 3.1 0 2 и и 3,5 ), то с учетом условия физической реализуемости фильтра ( h(t) 0 при t 0 ), момент максимального отношения сигнал/шум можетбытьдостигнутпри t0 0 и. Физическиэтоозначает, чтотолько вэтомслучаедляформированиямаксимальногопикасигналанавыходе может быть использована вся энергия входного сигнала s(t) — фильтр какбы «накапливаетсигнал». Увеличение t0 свыше( 0 и ) неизменяетвеличинупика. Он лишьпозжепоявится на выходе; и это, какправило, нежелательно.

ПрипроектированииРТСудобноиспользоватьотношениесигнал/шум, пересчитанноековходусистемы. Выполнимэтодлясогласованногофильтра. Пусть Fэ — эффективная полоса пропусканияСФ, равная эффективнойширинеспектрасигнала s(t). Мощностьшуманавходевэффективной полосе пропускания СФ равна Pn N0 Fэ а мощность сигнала

на входе СФ равна Ps Es / Tэ , где Tэ — эффективная длительность сигнала. Подставляя эти величинывформулу (3.21), получим

79

стейсигнал/шумсоответственнонавходеивыходеСФ. Изсоотношения

(3.23) следует, чтопризаданнойэнергиисигнала Еs иравномернойспек- тральной плотности мощности шума, равной N0, увеличение Fэ

иTэ порознь не влияет на отношение сигнал/шум на выходе СФ. Это отношение можно увеличить за счет увеличения базы сигнала.

Таким образом, использование сложных сигналов в РТС и применение СФобеспечиваетработоспособностьсистемприотношениисигнал/шум на входе в 2В разменьшем требуемогона выходесистемы. Эти выводы справедливы, если помеха (шум) является аддитивной гауссовской

и«белой», а форма полезного сигнала полностью известна.

Взаключениеотметимважноеобстоятельство. Сравнениевыражения

(1.10) для сигнальной функции q( x) , определяющей функцию различия сигналов ( x) по параметру х или по сообщению , связанному с ним, с сигнальной функцией zs (t, ) , формируемой на выходе СФ, показывает:

1) cреднее напряжение на выходе СФ в момент отсчета t t0 пропорционально величине сигнальной функции q( ), определяющей степень различия двух сигналов s(t, ) и s(t, 0 ), где 0 ;

2)формированиесигнальной функции q( ) сиспользованиемСФ предполагает«развертывание» напряжениянавыходефильтрапо , что вобщемслучаесвязаносприменениемсовокупности СФ, настроенных наразличныезначениясообщения ;

3)сигнальная составляющая напряжения на выходе СФ повторяет поформевременнуюАКФсигнала s(t);

4)величинамаксимальногоотношениясигнал/шумнавыходесогласованногофильтранезависитотформыполезногосигналаиопределяетсятолькоегоэнергией и спектральной плотностьюшума на входе.

80

3.3.Примеры построения согласованных фильтров

3.3.1. Согласованный фильтр для прямоугольного радиоимпульса

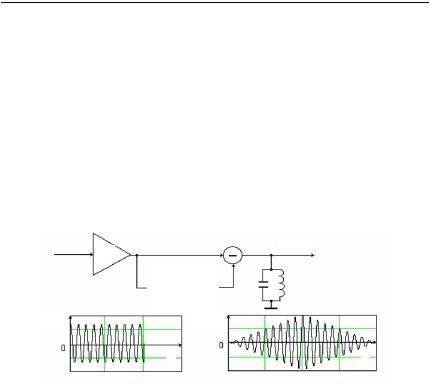
На рис. 3.2 показана структурная схема устройства, реализующего функции СФ, когда на его вход воздействует сигнал вида s(t) S0 cos( 0t) при t 0, и . Оно состоит из усилителя, линии задержки на время и , вычитающего устройства и колебательногокон-

и

Рис. 3.2. Согласованный фильтр для прямоугольного радиоимпульса

Пусть на вход устройства поступает прямоугольный радиоимпульс, тогданаконтуревысокойдобротностипроисходитлинейноенарастание амплитудынапряжениявтечениедлительностиимпульсасигналаивесьма медленное затухание колебаний после его окончания. В результате вычитания двух переходных процессов на выходе получается треугольный импульс (см. рис. 3.2), повторяющий по форме АКФ сигнала. При этом максимальное значение импульса в момент t и равно энергии

Еs c2 (S02 / 2) и .

Винженернойпрактикечастоиспользуютприближеннооптимальные фильтры(квазиоптимальные), посколькуихреализацияоказываетсяпроще. В частности, для прямоугольного радиоимпульса можно использоватьполосовойфильтрсАЧХ, близкойкпрямоугольнойформе, илиней-