
Статистические методы обработки сигналов в радиотехнических системах
..pdf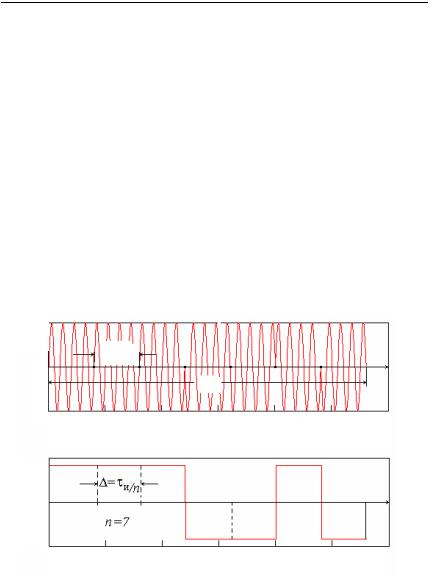
41
P (t) |
P t (i 1) 1, |
(i 1) t i , |
i |
|
(1.35) |
|
0 |
при других t. |
Наибольшее применение получили ФКМ-сигналы, фазы которых могут принимать только два значения: 0 или (бинарные коды). Если в сигнале используется большее число значений фаз i в пределах (0; 2 ), то такие сигналы называются многофазными. Учитывая, что изменениефазына приводиткпеременезнакаВЧ-заполнениянапро- тивоположный, сигнал (1.34) сбинарным фазовым кодомимеет вид
s(t) П(t)sin( 0t), |
(1.36) |
где П(t) — последовательность (импульсно-временной код), состоящая изn единичныхположительныхиотрицательныхимпульсов. Вкачестве примера на рис. 1.15,а показан радиоимпульс c бинарным фазовым кодом Баркера (n 7) и соответствующая ему модулирующая последовательность П(t). Кодовую последовательность символов можно услов-
нозаписать в виде: +1+1+1–1–1+1–1 (рис. 1.16).
s(t) 1
и/n
0
и
–1 |
1 |
1,5 |
2 |
2,5 |
||||
0,5 |
|
|||||||
|
|
|
|
|
|
а |
s(t) П(t)sin(2 f0t) |
|
1 |
|
|
|
|
|
|
|
|
П(t) |
|
|
|
|
|
|
|
|
|
и/n |
|
|
|
|
|||
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 7 |
|
|
|
|
|
–1 |
|
|
|
|
1 |
1,5 |
2 |
2,5 |
0,5 |
|
|||||||
б
Рис. 1.15. Радиоимпульсы с ФКМ (а)
и функция модуляции (манипуляции) фазы П(t) (б)
t
t
Определим главное сечение ФН при 0 , тоесть функцию K( ) . Если согласноформуле (1.15а) перемножить двесдвинутых повремени

42
на разные величины функции вида (1.36) и выполнить интегрирование (рис. 1.16,а), то получим, как и в случае одиночного прямоугольногорадиоимпульса (см. рис. 1.9,а), огибающую АКФ треугольного вида. Существенноеотличиебудетвтом, чтодлясигналасФКМфункция K( ) будет иметь 7 (почислу парциальных импульсов) максимумов (лепестков). Максимум главного лепестка ( 0 ) при отсутствии в (1.15а) нормировкиравен nE1 7E1 , где E1 — энергияпарциальногоимпульса длительностью . Максимумы шести боковых лепестков одинаковы и равны E1 . Эти лепестки получатся при сдвиге , кратном 2 , когда числосовпадающихпофазе i парциальныхимпульсовравно1. ВнормированномвидеАКФпоказананарис. 1.16,б. Еепротяженностьвсилу конечнойдлительностисигналаравна 2 и.
K( )
|
и n |
|
1 |
|
n 7 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
– и |
|
|
|
|
|
|
и |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
/n |
||||||
|
|
|
0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
а |
|
|
|
|
|
б |
|
|
|
|||||
Рис. 1.16. Главное сечение K( , 0) K( ) ФН радиоимпульса с ФКМ:
а— условное изображение двух копий сигнала;
б— огибающая временной АКФ-сигнала
СравнимАКФ K( ) (см. рис. 1.9,а) — сигнала спростой модуляцией и прямоугольной огибающей — сАКФаналогичногоподлительности, но сложного сигнала с ФКМ (см. рис. 1.16,б). Видно, что ширина второй из них, определяемая по первым нулям, равна 2 и / n , а первой — 2 и . Таким образом, АКФ K( ) сигнала с ФКМ сжимается в n 7 раз по сравнению с длительностью сигнала. Если учесть, что ширинаспектрасложногосигнала сФКМ F 1/ иегодлительностьT n , тобазасигнала B F T n , тоестьравнакоэффициенту сжатия.
ПрипрактическомпримененииФКМ-сигналовважнообеспечитьтре- буемый уровеньбоковыхлепестковФН. Какпоказановыше, он зависит отчисла парциальныхимпульсови равен 1/n. Таким свойствомоблада-

43
ют и другие коды Баркера [6]. Они могут быть построены только для n 13. Дляполучениябольших n применяютдругиекоды(вчастности, М-последовательности), у которых ФН (главное сечение при 0) в промежуточных точках не превышает 1/ 
 n . Известны М-последова- тельности, состоящих изнесколькодесятков тысячэлементов.
n . Известны М-последова- тельности, состоящих изнесколькодесятков тысячэлементов.
При больших n и / ФКМ-сигнал имеет высокую информативность и вместе с этим высокую надежность, определяемую малым уровенембоковыхлепестков, чтопозволяетоднозначноразличатьсигналы, отличающиесядруг отдруга большими сдвигами повремени.
Второе главное сечение ФН K( ) — огибающая частотной АКФ сигнала, как было показано выше, не зависит от фазовой структуры ВЧ-сигналаиопределяетсякакФурье-преобразованиеотквадратамоду- ля комплексной огибающей радиосигнала (1.26). Таким образом, для сигнала сФКМ и огибающей прямоугольной формы, получаем
K(F) |
sin( F и) |
|
, при F ( , ). |
|
F и |
||||
|
|
|||
Ширина этой функции по первым нулям равна 2/ и , |
Гц (см. |
рис. 1.9,б). Например при и 10 мсимеем FK 200 Гц |
и, если |
n 104, то и / n 2 мкс; автокорреляционная функция K( ) такого сигнала в 104 раз уже, чем АКФ равного по длительности сигнала без ФКМ.
Рассмотрим статистические свойства типовой случайной помехи — собственногошума приемно-усилительныхустройств.
1.4.Стационарная случайная помеха
сгауссовским распределением вероятностей. Белый шум
Увеличениюдостоверностиискоростипередачиинформациивсистемах связи и точности измерения координат объектов в РЛ- и РН-систе- махпрепятствуюттрифактора: 1) неизбежноеналичиевнешнихивнутреннихпомех; 2) искажения сигналовпри распространении радиоволн; 3) техническое несовершенствоустройств.
Улучшение параметров радиоэлементов и применение цифровой техники существенно снизили влияние последнего фактора. Внешние помехипоступаютнавходприемникавместесполезнымсигналом. Они

44
возникаюткакследствиеестественныхэлектромагнитныхпроцессов, происходящихватмосфере, ионосфереикосмосе, атакжеврезультатепреднамеренныхдействийпротивникапосозданиюпомех(пассивныеотражателиигенераторыпомех).
Нарядусвнешнимипомехамиимеютсявнутренние, которыевозникают в различных элементах передающих и приемных устройств. К ним относятсяфлуктуационныешумыламп, полупроводниковыхприборови сопротивленийпотерь, нестабильностинапряженийпитания, микрофонныйэффектидр. КонкретныйвидпомехзависитотусловийработыРТС. Однакообщим и характернымявляется наличие собственногофлуктуационного шума приемника и теплового шума пространства, окружающегоприемнуюантенну. Этишумыаддитивносмешиваютсясполезным сигналомна входеприемника.
Полноестатистическоеописаниеслучайнойпомехиx(t) предполагает задание n-мерной совместной плотности распределения вероятностей
(ПРВ) W (x1, x2 ,..., xn ;t1,t2 ,...,tn ), где x(ti ) xi |
(i 1,..., n) — значениепо- |
мехи в момент времени ti . Во многих практически важных случаях
помеха может рассматриваться как случайный стационарный процесс
(ССП) сгауссовским распределением вероятностей. Напомним кратко вероятностныйсмыслэтихпонятий.
Свойство стационарности случайного процесса состоит в том, что видn-мернойфункцииПРВW( ) неизменяетсяприпроизвольномпереносеначалаотсчетавремени. ДругимисловамиПРВнеизменится, если всемоментывременисместитьнапроизвольнуювеличину t . Этоозначает, чтоодномерная ПРВ W(xi;ti) W(x) не зависит от времени, тоесть в каждый отдельный момент времени случайный процесс x(t) имеет одинаковыевероятностныесвойства. Важнымипараметрамистационарнойпомехиявляются: среднийпоансамблюреализацийуровень— математическоеожидание
M x(t) x(t) xW (x)dx const
исредняяпоансамблюполнаямгновеннаямощность M x2 (t) x2 (t)
x2W (x)dx const.

45
Видно, чтоэтипарметрынеизменяютсявовремени. Помеха, воздействующая на вход приемных устройств РТС, в большинстве случаев не имеет постоянной составляющей, те. . ее среднее значение x(t) 0. Далееэтоусловиебудемсчитатьвыполненным.
Одномерная ПРВ не позволяет описать характер развития процесса вовременитоестьскоростьегоизмененияи, соответственно, спектральные свойства. Дляэтогонеобходимопривлечь хотябы двумерную ПРВ, которая для ССП зависит не от двух моментов времени t1 и t2 , а от их разности t1 t2 , причемзнак неимеетзначения. Такимобразом, АКФстационарнойпомехисосреднимзначением, равнымнулю, есть
Kx (t1,t2 ) x(t1) x(t2 ) x1x2W (x1, x2;t1,t2 )dx1dx2 Kx ( ) . (1.37)
Случайныйпроцессназываютгауссовскимилинормальным, еслиПРВ произвольногопорядка имеетвид квадратичной экспоненты. Одномер-
наяПРВв этомслучаеравна (при x(t) 0 )
|
|
1 |
|
|
x2 |
|
|
|
||
W (x) |
|
e |
2 |
2 |
, |
x ( , ), |
(1.38) |
|||
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
||
где — среднеквадратическоезначениепомехи(эффективноезначение переменной составляющей процесса). Двумерная ПРВ представляет собой гауссовскую поверхность
1
W (x1, x2 ; ) exp 0,5Q(x1, x2; ) , (1.39) 2 2  1 kx2 ( )
1 kx2 ( )
где kx ( ) Kx ( ) / 2 — нормированная автокорреляционная функция помехи; квадратичнаяформавпоказателеэкспонентыимеетвид
|
|
|
x 2 |
2x x k |
x |
( ) x 2 |
|
|
|
Q(x , x |
2 |
; ) |
1 |
1 2 |
|
2 |
. |
(1.40) |
|
|
|
|
|
|
|||||
1 |
|
|
2[1 kx |
2 |
( )] |
||||
|
|
|
|
|
|
||||
В n-мерном случае форма (1.40) имеет аналогичную структуру: содержитвчислителевторыестепенивсехпеременных xi , атакжеперекрестные слагаемые вида aij xi x j , где aij 2k(t j ti ) — коэффициенты, определяемыевидомАКФ; знаменательравеннекоторойпостояннойвеличине, определяемой конкретным выбором t1,t2 ,...,tn . Таким образом,
длязаданияn-мернойПРВгауссовскойпомехидостаточнознанияАКФ помехи Kx ( ) .

46
Нормальный стационарный случайный процесс имеет несколько примечательныхсвойств.
1.Статистическиесвойства процесса полностью и однозначноопре-
делены заданием его АКФ, так как знание Kx ( ) позволяет записать n-мернуюПРВ.
2.Статистическая независимость совокупности отсчетов xi гауссовского процесса в n моментов времени следует из соотношения
kij k(t j ti ) xi x j 0 для i, j 1,…,n. Для n 2 этот выводследует из сопоставления (1.38) и (1.39). Действительно, если при некотором
функция kx ( ) 0, то W (x1, x2 ) W (x1) W (x2 ), аэтоестьусловиестатистической независимости случайных величин x1 и x2 . Таким образом, совместная ПРВ системы n взаимно некоррелированных гауссовскихслучайныхвеличинравна
n |
|
W (x1, x2 ,..., xn ) W (x1) W (x2 ) W (xn ) W (xi ) . |
(1.41) |
i 1 |
|
Подставляяв (1.41) выражениеодномерной ПРВиз (1.38), получим
|
|
|
|
1 |
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
2 |
|
|||||
W (x1, x2 |
,..., xn ) |
|
|
|
|
exp |
|
|
|
xi |
. |
(1.42) |
|
n |
(2 ) |
n / 2 |
2 |
2 |
|||||||
|
|
|
|
|
|
|
i 1 |
|
|
|||
3. При линейном преобразовании гауссовского процесса свойство гауссовости сохраняется, изменяется тольковид АКФ Kx ( ) .
ОсобоеместонормальныхпроцессоввзадачахсинтезаианализаРТС обусловлено тем, что реальные радиопомехи и, в частности, собственный шум приемно-усилительных устройств, образуются в результате суперпозиции большого числа случайных элементарных колебаний. В итогевероятностные свойства суммарногопроцесса всилуцентральнойпредельнойтеоремытеориивероятностейудовлетворительносогласуютсясосвойствамигауссовскогопроцесса. Напомним, чтосмыслупомянутойтеоремысводитсякутверждениюасимптотическойнормальности суммыслучайныхслагаемыхспроизвольнымиПРВпомереувеличения их числа.
Спектральныеметодыанализавоздействияпомехнахарактеристики РТСоснованынаизвестнойтеоремеВинера— Хинчина, всоответствии скоторойдляАКФстационарногослучайногопроцессасправедливапара преобразованийФурье

47
K ( ) |
1 |
|
G ( )ei d |
и G ( ) |
|
K ( )e i d , (1.43) |
|
2 |
|
|
|||||
x |
x |
x |
x |
||||
|
|
|
|||||
|
|
|
|
|
где Gx ( ) — спектральнаяплотностьмощностипомехи. Размерность этой функции можно установить, записав соотношение для средней мощности помехи Kx (0) 2 , Вт . Из (1.43) получаем Kx (0)
|
1 |
|
|
|
|
|
Gx ( )d , т.е. подынтегральноевыражение Gx ( f )df имеетсмысл |
||||
2 |
|||||
|
|
df вблизи частоты |
f. |
||
средней бесконечно малой мощности в полосе |
|||||
Следовательно, функция Gx ( f ) измеряется в ваттахна герц, или джоулях, поэтомуфункцию Gx ( ) называюттакже энергетическимспект- ром помехи, или коротко — спектром помехи. Физический смысл этого понятия следует из того, что ССП x(t) состоит из непрерывного множествагармоническихсоставляющихсослучайнымиамплитудамиифазами, ихсредняямощностьвполосе df вблизи частоты f равна Gx ( f )df .
Рассмотримстационарнуюпомеху, спектркоторойможносчитатьпочти постоянным вплоть до некоторой верхней частоты в 2 fв , вблизи которойспектрпадаетдонуля. Зададимтакойспектрсоотношениями
|
Gx ( ) |
N0 |
, |
|
|
|
в; |
|
Gx ( ) 0, |
|
|
|
в , |
|
|
|
|
(1.44) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где N0 — спектральнаяплотностьпомехи. Спомощью(1.43) найдемАКФ |
||||||||||||||||||||||||||
|
N |
|
в |
|
|
|
|
N |
|
|
sin |
|
|
|
|
|
N |
|
|
|
|
|||||
|
0 |
|
ei d |
в |
|
|
|
|
в |
|
|
|||||||||||||||
Kx ( ) |
|
|
0 |
|
|
в |
|
; Kx (0) 2 |
0 |
|
. |
(1.45) |
||||||||||||||
2 2 |
2 |
|
в |
|
2 |
|
||||||||||||||||||||
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
На рис. 1.17 и 1.18 представлены спектри АКФ помехи для следующихзначенийпараметров: N0 10 8 Дж; fв 100 МГц.
Корреляционнаяфункцияпри 0 имеетпик, величинакоторогоравнасреднеймощностипомехи. Функция Kx ( ) , осциллируя, уменьшается ориентировочнокак функция 1 . Из формулы (1.45), и это подтверждает рис. 1.18, следует, что случайные отсчеты помехи x(ti ) xi , (i 1,..., n) , соответствующие моментам времени ti , которые разделены промежутками, кратными t / в, строго некоррелированы. Вприведенномпримере t 1/(2 fв) 0,005 мкс .
В инженерных расчетах особое значение имеет предельный случай, когда fв . Практически эта ситуация возникает, когда верхняя

48
частота помехи fв многобольшечастотсигналов, на которыерассчитана РТС. Для предельного случая АКФ помехи
|
|
N |
|
|
sin |
|
|
N |
|
|
|
|||
Kx ( ) |
lim |
|
0 |
|
в |
|
в |
|
|
|
|
0 |
( ), |
(1.46) |
|
в |
|
|
|||||||||||
2 |
|
2 |
||||||||||||
|
в |
|
|
|
|
|
|
|
||||||
где ( ) — -функцияДирака. Помеха, имеющаяАКФвида(1.46), назы- вается белым шумом. Таким образом, у белого гауссовского шума любыедва скольугодноблизкихповременизначениянекоррелированы и, следовательно, статистическинезависимы.
|
|
8 |
if |
|
f |
|
100 |
|
|
|
|
||||||
|
10 |
|
|
|
||||
Gx |
( f ) |
|
|
|
|
|
|
|
otherwise |
||||||||
|
0 |
|||||||
|
|
|
|
|
|
|
|
|
1 10–8
Gx ( f )
0
–100 |
0 |
100 |
|
f, МГц |
|
Рис. 1.17. Энергетический спектр шума с ограниченной полосой частот
Kx ( ) sin(2 fв ) /(2 fв )
1
Kx ( ) fв 100 МГц 0,5
0
–0,02 –0,01 |
0 |
0,01 |
0,02 |
, мкс |
|
||
Рис. 1.18. Автокорреляционная функция шума с ограниченной полосой частот
Вприемныхустройствахначастотахвыше 30–50 МГц собственный шумпревышаетуровеньвнешнихестественныхпомех. Егомощность
Pш 2 kT Fэkш,
где k — постоянная Больцмана, равная 1,38 10 23 Дж/К; T — температуравградусахКельвина; kш — коэффициентшумаприемника; Fэ — эффективнаяполосапропусканияприемника. Допустим, вРЛСиспользуется импульсный сигнал со сложной модуляцией: база В 104;и 1 мс; kш 3 . Тогда полоса Fэ составит 10 МГц и мощность шума на входеприемника Pш 1,38 10 23 107 300 3 12,5 10 14 Вт.

49
1.5.Контрольные вопросы
1.Вчемпринципиальноеотличиесигналаипомехи?
2.ПочемуРТС извлечения информации относят к системам с внешней модуляцией, а РТС передачи информации — ксистемам свнутреннеймодуляцией?
3.Вчемотличиеаддитивнойпомехиотмультипликативной?
4.В чем различие детерминированного и статистического подходов к решению задач анализа и синтеза РТС? Почему детерминированный подходнесостоятелен?
5.Перечислитефункцииипараметры, заданиекоторыхсвязаноспонятиемстатистическогоописанияслучайнойфункции.
6.Вчемотличиедетерминированной, квазидетерминированнойислучайнойфункций?
7.Вчем отличиеаналоговогои цифровогосообщений?
8.Запишитеобщеевыражениесигнала-переносчикасообщения.
9.В чем отличие сигналов с одноступенчатой и двухступечатой модуляцией? Приведитепримерыосциллограмм.
10.Чтоесть функция различия сигналов и каков ее смысл?
11.Запишитевыражениефункцииразличиядвухсигналовпоодному информативному параметру x, когда он не является энергетическим. Подвумпараметрам?
12.Запишите в общем виде частотно-временную корреляционную функциюузкополосногорадиосигнала.
13.Запишите выражение временной автокорреляционной функции узкополосногорадиосигнала в действительной и комплексной форме.
14.Запишите выражение комплексной огибающей временной АКФ узкополосного радиосигнала и обоснуйте тот факт, что это медленная (в сравнении с cos( 0t) ) функция времени.
15.Чтоестьфункциянеопределенностирадиосигнала, каковыеесвой-
ства?
16.Вчемсущностьпринципанеопределенностиврадиолокации?
17.КакиепараметрырадиосигналаопределяютширинуФНвдольосей «время— частота»? КаквлияетэнергиясигналанаФН?
18.Чтоестьбаза радиосигнала, ивчемразличиесигналовспростой исложной модуляцией?

50
19.Почемудля сигнала с простой модуляцией уменьшение ширины пика ФНпооси временипри постоянной мощности непременноприводиткснижениюэнергииэтогосигнала?
20.Почему для сигнала со сложной модуляцией уменьшение ширины пика ФН по оси времени при постоянной мощности не приводит кснижениюэнергииэтогосигнала?
21.Вкаком случаеширина огибающей радиосигнала и ширина огибающей временной АКФ примерноодинаковы? Когда они могут различатьсяна несколькопорядков?
22.ИзобразитеграфическивременнуюАКФодиночногорадиоимпульса спрямоугольной огибающей и простой модуляцией.
23.ИзобразитеграфическивременнуюАКФодиночногоФКМрадиоимпульса с прямоугольной огибающей? Какова величина боковых максимумовэтой функции посравнениюсглавнымпиком?
24.Почемудляполнотывероятностногоописанияслучайногосигнала необходимо привлечение плотностей распределения вероятностей более чем 1-го порядка?
25.Какаяфункцияопределяетспектральныесвойстваслучайногостационарногопроцесса? Пояснитееевероятностныйсмыслиукажитефизическуюединицуизмерения.
26.Какой случайный процесс называют нормальным, каковы его особенности?
27.Чтоозначаеттотфакт, чтошумбелый?
28.Чтоозначаеттотфакт, чтошумстационарныйи гауссовский?
29.Какоевлияниеоказываетфазоваяиличастотнаямодуляциясигналанавидчастотнойавтокорреляционнойфункциисигналаипочему?
