Статистические методы обработки сигналов в радиотехнических системах

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

K( ) exp 0,5 k2

K( ) exp 0,5 k2

На рис. 1.13 функция K( )

показана в виде огибающей для АКФ

..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

6.9 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 254 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

						31
то есть зависит от вида функций		(t)	2	и			2
			2				2
	S				G( )		. Физический смысл

соотношения (1.17) состоит в том, что полная энергия Es непрерывно распределенаповремениилипочастоте, тоестьвспектральнойобласти. В бесконечно малом интервале dt в момент времени t ее величина dE(t) 0,5S2 (t)dt; вбесконечномалойполосечастот df 1/ 2 d —

dE( f ) 0,5		2
		2
	G( f )	df . Умножение на 0,5 обусловлено использованием

комплексногопредставлениясигналов: мнимаяидействительнаясоставляющиекомплекснойамплитудысигналаимеютравныеэнергииисоответственноравноправны положительныеи отрицательные частотыпри спектральномпредставлениидействительногосигнала.


Введем два параметра, которые характеризуют функции				2
				2
			S(t)	и
	2	Т иширинуполосычастотногоспектра
	2
G( )	: длительностьсигнала

сигнала . Математическиевыкладкивыполняютсяпросто, если начало отсчета времени и частоты поместить в точки, соответствующие «центраммасс» фигур, образуемыхнормированнымифункциями

	2		2
S(t)		G( )

			и					.	(1.18)
		2	и					.	(1.18)
							2
							2
	S(t)	dt				G( )	d

В этом случае величины			T 2	и	2		могут быть определены как

меры рассеяния (дисперсии) соответствующих функций (1.18). В итоге получаем

		2				2
	t	2				2
Т2	t			S(t)		dt

					2

						dt
			S(t)			dt

		2			2
		2			2
2			G( )		d
2
и	=					.	(1.19)
и	=			2		.	(1.19)
				2	d
		G( )			d

Параметры Т и 2 F характеризуютрассеяниеВЧ-сигна- ла во времени и по частоте (относительно несущей 0 ). По аналогии ссоответствующейвеличинойвтеориивероятностейихназываютсред-

неквадратическими длительностью и полосой частот сигнала. Эти параметры определяют помехоустойчивостьи точность РТС различных типовприналичиипомех. Заметим, чтовэнергетическихрасчетахчаще

используютпонятие эффективнойдлительности сигнала Tэ , которое более наглядно. Величина Tэ определяет энергию Es P Tэ , где Р — средняя мощность сигнала. Физически реальные сигналы имеют конечную энергию, поэтому для функций s(t) с конечной длительностьюисоответственноснеограниченнымпополосечастотнымспектромTэ равнофактическойдлительностисигнала Ts .

Если функция s(t) неограничена во времени и имеет конечную среднюю мощность, ее эффективную длительность определим

иначе. Пронормируем функцию s(t)						и представим огибающую S(t)
			S 0 (t ), где	S0 (t)	— нормированная (не имеющая размер-
	2 Р
							S02 (t)dt и, очевидно, ES
ности)		огибающая,		причем Tэ

			S 2 (t)dt P Tэ .
0, 5					Величину		Tэ , имеющую размерность

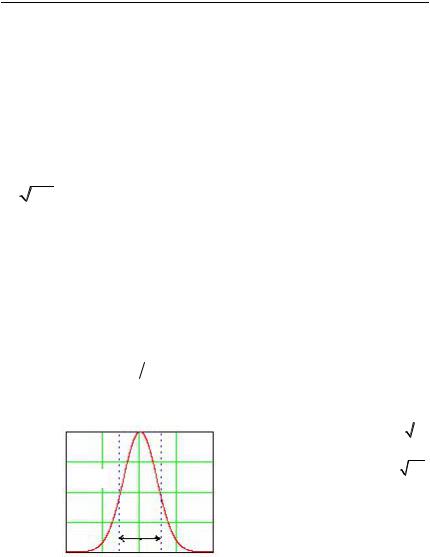
времени, иногданазывают интегральнойширинойсигнала. Смыслэтой величины для импульса гауссовской формы поясняет рис. 1.6, из кото-

рогоследует, что Tэ

2 и равнооснованиюпрямоугольника, площадь

которого также равна 2.

Конечно, величины Tэ и T взаимосвя-

S (t) exp t2 4 T2

заны. Например для радио-

импульса с прямоугольной оги-

(t)dt 2

бающей, имеющейдлительность

Tэ TS , среднеквадратическая

длительность T Tэ / 2

3 ;

0,75

для радиоимпульса с гауссов-

Sn2 (t)

скойогибающей T Tэ /

Tэ3

f (t) 0,5

[8].

0,25

Кчислуосновныххарактери-

стиксигнала относитсявеличи-

наВ— базасигнала, равнаяпро-

изведениюсреднеквадратичной

–3,5 –1,75

1,75 3,5

длительности сигнала на сред-

неквадратичную ширину его

Рис. 1.6. Эффективная

спектра:

длительность Тэ сигнала

с нормированной огибающей S0(t)

B T F T / 2 .

В теории сигналов показано, что для любых сигналов значение базы B (1/ 4 ) [6]. Неравенство B (1/ 4 ) известно как соотношение неопределенностей.

Взависимостиотвеличиныбазысигналыбывают простые и слож- ные. Для реальных сигналов с простой модуляцией В имеет порядок единицыипрактическинезависитотспособаопределенияихдлительности и ширины спектра, у сложных — база B 1. В отличие от минимального значения базы, ее максимальное значение теоретически неограничено. Практическиеограниченияприиспользованиисигналов сбольшойбазойсвязанысаппаратнойреализациейустройствформирования сложных сигналов. В настоящее время в РТС используются ЧМ- и ФМ-сигналы, база которыхимеет порядок 105.

Рассмотрим параметрическое описание ФН радиосигнала, содержащего сообщение в виде задержки и частотного сдвига , те. . найдем представление ФН через параметры сигнала Т и F. Если функцию

K ( , F) 2 в окрестности точки ( 0; F 0) разложить в двойной ряд Тейлора и ограничиться членами не выше второго порядка (квадратичноеприближение), томожнополучитьследующеесоотношение [6, 8]:

K ( , F )		2 1 F 2 2 2 F T 2 F 2 ,	(1.20)

где F / 2 ; — коэффициентчастотно-временнойсвязи,

2				2
		t Ф (t)	S(t)

				dt .	(1.21)
2E
	s

Из (1.21) следует, что 0, если сигнал не имеет фазовой модуляции, тоесть Ф (t) 0 . Дляопределенияпараметров, характеризующих ширину пика ФН, приравняем левую часть (1.20) уровню с2. В итоге получаемуравнениелинииуровня. Поформеоносовпадаетсуравнением эллипса. Анализпоказывает, чтоширина эллипса вдоль оси временной задержки и соответственноширина центральногопика функции неопределенностивдольоси равна

				2	1 c2
						,	(1.22)
						,	(1.22)
					F
и при c2 0,75 имеем	=	1	.
и при c2 0,75 имеем	=		.
		F

Ширина эллипса и, значит, ширина пика ФН вдоль оси частот F составляет

	2	1 c2
F			,	(1.23)

		T

при c2 0,75	F	=	1	.

			T

Величины и F , определяяширинуглавныхсеченийФН, равны соответственноширинеогибающейвременнойичастотнойАКФсигнала. Этидва параметраиграютважнуюрольприрасчетепотенциальных характеристикРТС.

Проведенныйанализпозволяетсделатьследующиевыводы.

1.Уменьшениеширины главногопика ФНвдоль оси времени эквивалентносужениюогибающейвременнойавтокорреляционнойфункции K( ) и возможнопри расширении частотногоспектра ВЧ-сигнала s(t).

2.Для простых ВЧ-сигналов, имеющих базу B T F 1, расширение частотного спектра связано с уменьшением их длительности, чтоприпостоянноймощности Р ведеткуменьшениюэнергиисигнала

ES P T ивсоответствиис принципомнеопределенностивозрастаниюшириныглавногопикаФНпоосичастот.

3.Применение сложных сигналов ( B 1) позволяет расширить частотный спектрсигнала и темсамымуменьшитьширинуогибающей временнойАКФK( ) приодновременномувеличениидлительностисигнала, что дает возможность повысить энергию сигнала без увеличения егомощностии уменьшитьширинупика ФНпооси частот.

1.3.4.Примеры функций неопределенности импульсных сигналов

РассмотримФНтипичныхимпульсныхрадиосигналов.

Радиоимпульс с прямоугольной огибающей и простой модуля-

цией. Представимсигнал, имеющийамплитуду S0 , начальнуюфазу 0 и длительность TS и в виде

s(t) Re S(t)ei 0t ,

где

S(t)

ei 0

rect

;

при

0,5

rect(x)

0,5

Введеннаянормировка

и / 2

0,5

прямоугольная функция

обеспечиваетвеличинуэнергии

S(t) 2 dt 1.

и / 2

Радиоимпульс

s(t)

при

0 ,

S(t)

и 1 показан на рис. 1.7. Подстав-

ляяв (1.15) выражениеегокомплекс-

–1

нойогибающейи выполняяинтегри-

рование, получимФНпрямоугольного

–2

–0,5

0,5

радиоимпульса в виде [2, 6]:

–1

Рис. 1.7. Прямоугольный

радиоимпульс s(t)

K( , F)

sin F

)

и.

(1.24)

F и(1

/ и)

Поверхность, соответствующая ФН (1.24) имеет явно выраженный главный максимум (рис. 1.8,а). Вдоль оси временной задержки ФН имеетконечнуюпротяженность, чтоследуетизспособаобразованиякорреляционной функции. Действительно, в (1.15) в подынтегральном выражении огибающая S(t) умножается на свою копию S(t – ), сдвинутую по оси времени на , и при и результат интегрирования равен нулю. На рис.1.8,б показаны проекции сечений K( ,F) const на плоскость (FO ) — линии уровня. Видно, чтовобласти высокой корреляции (0,6–0,7 и выше) линии уровня близки к окружностям.

На рис. 1.9,а приведены сечения ФН K( ) K( , F const) — огибающиевременнойкорреляционнойфункцииприразличныхзначениях допплеровского сдвига. При F 0 получаем огибающую временной АКФпрямоугольногорадиоимпульса, котораясогласно(1.24) имеетвид

				K( ) 1							,	и, и .					(1.25)
				K( ) 1							,	и, и .					(1.25)
									и
K( ,F)													–2
0,8													–1	F
0,6													–1
0,6
0,4													0
0,2													1

0												1
0												1

–2										0,5
													2
	–1							0



		0
							–0,5						–1	–0,5	0	0,5	1
			1

					2

						F
			а												б

Рис. 1.8. Функция неопределенности прямоугольного радиоимпульса: а — поверхность ФН (огибающая частотно-временной корреляционной функции); б — линии уровня функции неопределенности

K( )					K(F)
				0
	При F			0		0
0,75	При F				0,75	0

			0,5
0,5					0,5
0,25					0,25
0		0,5			0
–1 –0,5 0		0,5			–4 –2 0 2 F
				а		б

Рис. 1.9. Сечения огибающей частотно-временной корреляционной функции радиоимпульса ( и = 1)

На рис. 1.9,б показано главное сечение ФН K( 0, F) K(F) — огибающая частотной автокорреляционной функции прямоугольного радиоимпульсаспростоймодуляцией. Выражениедлянееследуетиз(1.15) и согласно (1.24) имеет вид

и / 2

S(t)

i2 Ft

sin( F и)

, F , . (1.26)

K(F)

s и / 2

Соотношение (1.26) — преобразование Фурье от квадрата огибаю-

щей сигнала. Таким образом, частотная АКФ сигнала не зависит от его фазовой структуры и определяется только формой огибающей радиоимпульса.

На рис. 1.10 изображена временная АКФрадиоимпульса, соответствующаявыражениям(1.15а), (1.16). Онаявляетсячетнойосциллирующейфункциейсчастотой сигнала 0 и имеет конечную длительность, вдвоепревышающуюдлительность сигнала s(t). Следуетобратитьвнимание на то, что вблизи главного максимума функции k( ) расположены близкие по величине локальные максимумы, следующие через интервалы, равные периоду ВЧ-сигнала.

K( ,0)	F=0
0,5	F=0
0,5
0
–0,5
–1
–1 –0,5 0	0,5

Рис. 1.10. Корреляционная функция прямоугольного радиоимпульса и 1

Гауссовский радиоимпульс с внутриимпульсной линейной ЧМ.

ПредставимрадиоимпульссгауссовойогибающейилинейнойЧМ(ЛЧМ) в виде

s(t) S	m	e k2t2	cos(	t bt2	0	),	t , ,		(1.27)
	m		0		0

где S(t) Sm exp( k2t2 ) — огибающаярадиоимпульса; Sm — значение

огибающей в максимуме; k — параметр, определяющий длительность сигнала; b — параметр частотной модуляции. Мгновенная частота сигнала (1.27) изменяется по линейному закону (t) 0 2bt, где 2b — скорость изменения частоты. При длительности импульса T и девиации частоты M , скорость изменения частоты 2b M / T. Обычно ширина спектра сигнала с ЛЧМ равна девиации частоты, то есть M . Таким образом, база сигнала B F T 2b T2/2 . На

рис. 1.11 показан сигнал с ЛЧМ для значений S0 1,3; k 2мкс–1, b 20 рад/мкс. Расчет длительности сигнала по формуле (1.19) дает величину T 1/ 2k 0,25 мкс, то есть В 0,4. Конкретные величины параметровзаданыдляудобства восприятиярисунка.

S(t)

0,75

–0,75

–1

–0,5

0,5

Рис. 1.11. Радиоимпульс гауссовской формы с ЛЧМ

Подстановка в (1.15) комплексной амплитуды сигнала (1.27) дает выражениеФНввиде

K( , F) exp

0,5

k2 2

, F , . (1.28)

Уравнению (1.28) соответствует гауссовcкая поверхность ФН (рис. 1.12,а). На рис. 1.12,б показаны линии равного уровня. В данном случае их форма эллиптическая, это характерно для сигналов с ЛЧМ. Рассмотрим главные сечения ФН, поскольку они определяют ширину эллипсов вдоль главных осей и F. Из (1.28) при F 0 получаем огибающуювременной АКФгауссовскогорадиоимпульса

k( ) радиосигнала, которая, как и сам сигнал, является высокочастотной (см. 1.16). Необходимо отметить, что функция k( ) в отличие от сигнала s(t) не имеет фазовой модуляции.

Принципиально важным для построения оптимальных систем об- работкисигналовявляетсятотфакт, чтоогибающая K( ) оказыва- ется более узкой, чем огибающая S(t) исходного радиоимпульса. Это видно при сравнении рис. 1.11 и 1.13. Определим величину сжатия по

временифункции K( ) посравнениюс S(t) ввидеотношения kсж T ,

где T и — среднеквадратические длительности функций S(t) и

K( ) соответственно. Как было показано выше, T 1/ 2k . ВычислениедлительностиогибающейАКФсогласно(1.19) даетрезультат

	1			1				.	(1.30)


	2		k	2 1 16	2	B	2
k 2 1		b	k			B
k 2 1		4
		k

Витогекоэффициентсжатияфункции K( ) , равен

kсж

0,5 8 2B2 ,

(1.31)

отсюда при B 1 kсж 2 B2. Он фактическизависиттолькоотбазы сигнала.

K( ,F)
0,8
0,8		–3		0,33
0,6		–3
0,6		–2	F
0,4		–2	F		0,66
0,4		0
0,2		0
		2
	0
0	0
		3
		3

F	–0,4	0

				0,4	–0,8 –0,4 0 0,4 0,8
				0,4

			а		б

Рис. 1.12. Функция неопределенности радиоимпульса с гауссовой огибающей: а — поверхность неопределенности

(огибающая частотно-временной корреляционной функции); б — линии уровня функции неопределенности

Для гауссовского радиоимпульса с простой модуляцией база B T F 1/ 4 [6]. Согласно (1.31) в этом случае kсж 1 (сжатие отсутствует). В нашем примере B 0,4 и kсж 3,6 . В РТС применяются сигналы с базой донескольких сотен тысяч.

ВтороеглавноесечениеФН, соответствующееогибающейчастотной АКФ, получаем из (1.28). При 0 имеем

K(F)	K	( 0, F)		2F2			(1.32)

			exp 0,5			.
				k	2

Ширинаэтойфункциизависиттолькоотдлительностирадиоимпульса (параметр k). Таким образом, наличие любой ЧМ не изменяет ее вид, поскольку K( ) связана взаимным Фурье-преобразованием с функцией S(t) 2 (см. 1.26), которая неучитывает фазовый множитель комплексной огибающей. Функция (1.32) имеет также гауссовскую форму (рис. 1.14). Среднеквадратичная ширина функции K( ) , вычисленная по(1.19), даетрезультат

			F k	2 .			(1.33)
				K(F)
k( )	F=0			K(F)	0

			K( )	0,75
			K( )	0,75
0,5				0,5
0				0,5
0				0,25
–0,5				0,25
–0,5				0
–1 –1	–0,5	0	0,5	0			1 F
–1 –1	–0,5	0	0,5	–2	–1	0	1 F
Рис. 1.13. Временная АКФ					Рис. 1.14. Огибающая
	сигнала s(t) с ЛЧМ.				частотной АКФ сигнала
K( ) — огибающая АКФ						s(t) с ЛЧМ

Из (1.33) следует, что чем протяженнее радиосигнал, тем уже главный пик ФН пооси допплеровскогосдвига частоты.

Прямоугольный радиоимпульс с фазокодовой модуляцией. Рас-

ширениечастотногоспектрарадиоимпульсапризаданнойдлительности возможно как с помощью внутриимпульсной ЧМ так и ФКМ. Относительная простота фазовогокодирования сигналов и преимущества, связанныеспостоянствомамплитудыпри генерации и усилении сигналов, обеспечилиФМ-импульсамширокоеприменение. Радиоимпульспрямоугольной формы с ФКМ можнозадать в виде

n
s(t) Pi (t)sin( 0t i ),	0 t n ,	(1.34)
i 1

где n и — длительностьимпульса, составленногоизn парциальных импульсов, имеющихширину иначальнуюфазу i ; функция

<<< < Предыдущая 1 2 34 / 254 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20231.8 Mб7Статистические методы в управлении инновациями.-1.pdf
#
05.02.20231.84 Mб7Статистические методы в управлении инновациями..pdf
#
05.02.2023374.45 Кб5Статистические методы в управлении качеством.-2.pdf
#
05.02.2023239.46 Кб5Статистические методы в управлении качеством.-3.pdf
#
05.02.2023135.55 Кб4Статистические методы в управлении качеством..pdf
#
05.02.20236.9 Mб29Статистические методы обработки сигналов в радиотехнических системах..pdf
#
05.02.2023707.29 Кб13Статистические методы обработки..pdf
#
05.02.2023629.36 Кб6Статистические модели для информационных систем, квантовых и оптоэлектронных приборов..pdf
#
05.02.2023239.02 Кб6Статистические модели для систем передачи и обработки информации.-1.pdf
#
05.02.2023312.5 Кб8Статистические модели для систем передачи и обработки информации..pdf
#
05.02.2023299.57 Кб4Статистические модели квантовых, оптоэлектронных и акустооптических приборов.-1.pdf