
Статистические методы обработки сигналов в радиотехнических системах
..pdf
191
Вероятностноеописаниевысокочастотногосигнала, состоящего из суммы регулярной составляющей и стационарного узкополос-
ного гауссовского шума. Представим сигнал в виде суммы регулярногосигнала sрег(t) и случайного шума vсл(t)
s(t) sрег(t) vсл(t) Acos( 0t ) V (t)cos 0t (t) |
(8) |
иливравносильнойформе |
|
s(t) Acos V (t)cos (t) cos 0t [Asin V (t)sin (t)]sin 0t, |
(9) |
где A, — амплитудаифазарегулярнойкомпонентысигнала(постоянные величины); V (t), (t) — огибающая и фаза (случайные функции) узкополосного высокочастотного шума, энергетический спектр которого сосредоточен «вблизи» частоты 0 . Слагаемые в квадратных скобках соотношения (9) называют квадратурными компонентами
радиосигнала s(t). По условию случайный шум есть гауссовский про- цесс, поэтому его квадратурные компоненты Vx (t) V (t)cos (t) и Vy (t) V (t)sin (t) являются случайными совместно гауссовскими функциями. Перепишемвыражение(9) черезквадратурныекомпоненты радиосигнала s(t) в виде
где
Y
Uy
s(t) Ux (t)cos 0t U y (t)sin 0t U (t)cos 0t (t) , |
(10) |
||
|
Ux (t) Acos Vx (t) , U y (t) Asin Vy (t) . |
(11) |
|
|
V(t) |
На рис. 4 соотношения (9)–(11) пояс- |
|
|
(t) |
няетвекторнаядиаграммасигналов. |
|
A |
|
Зададим вероятностные парамет- |
|
U(t) |
ры шума. Будем считать, что шум vсл(t) |
||
|
|
имеет среднее значение, равное нулю. |
|
|
(t) |
Вэтом случаесреднеезначениеего квад- |
|
ратурныхсоставляющихтакжеравнонулю,
Ux |
X |
тоесть |
|
||||
Рис. 4. Векторная |
|
|
|
|
|
0 . |
(12) |
диаграмма |
|
|
Vx (t) |
Vy (t) |
|||
Положим, чтосредняя мощность шумовых квадратурных процессов Vx (t) V (t)cos (t) и Vy (t) V (t)sin (t) одинаковаиравнавеличине

192
2 Vx2 (t) Vy2 (t) . |
(13) |
Взаимныйковариационныймоментквадратурныхсоставляющихшума
KV V |
Vx (t)Vy (t) 0 , |
(14) |
x |
y |
|
тоестьонимеждусобойвсовпадающиймоментвременинекоррелированы.
Необходимообратитьвнимание, иэтоследуетиз (10), чтослучайная величинасигнала s(t) водин (любой) моментвремени t определяется значениемдвухслучайныхвеличин Ux(t) и Uy(t) вэтотжемоментвремени. Эти две величины определяют в (10) огибающую смеси регулярногосигнала и шума
|
|
|
U(t) Ux2 (t) Uy2 (t) |
|
|
(15) |
||||||||||
и фазу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uy (t) |
|
|
|
|
|
|||
|
|
|
(t) arctg |
|
|
|
. |
|
|
(16) |
||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
Ux (t) |
|
|
|
|
|
|||
Совместная ПРВ величин Ux (t) Ux |
|
и U y (t) U y |
в один момент |
|||||||||||||
времениимеетвид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
(u |
m |
)2 |
|
|
(uy my )2 |
|
|
|
|
|
|
|
1 |
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
W (ux |
,uy ) |
|
e |
|
2 2 |
|
|
e |
2 2 |
, |
(17) |
|||
|
|
2 2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где mx |
|
Acos и my |
|
Asin — средние(поансамблю) зна- |
||||||||||||
Ux |
Uy |
|||||||||||||||
ченияквадратурныхсоставляющихслучайногорадиосигнала s(t), зависящиеотамплитудыифазырегулярногокомпонентасигнала.
На рис. 5 показана структурная схема формирования случайного радиосигнала s(t), его огибающей U(t) и фазы (t).
Статистические свойства огибающей U(t) и фазы (t). Свойства огибающей и фазы изучаются в работе на уровне одномерных ПРВ
исоответствующих моментов — математических ожиданий U mU
иm (t) исреднеквадратичныхотклонений U и . Всенеобходи-
мые математические соотношения приведены в [1, подразд. 2.3]. Вид ПРВ W(U) и W( ), а также соответствующие моменты огибающей и фазы фактически определяются величиной a A/ , которая задает отношениеуровней регулярногосигнала и шума.

193
Векторная диаграмма на рис. 4 позволяет физически понять, чтопо мереувеличения A / интенсивностьвариацийкакогибающей U, таки фазы уменьшается. Средниезначения mU и m приближаютсясоответственноквеличинеамплитуды А ифазы регулярногосигнала.
|
Acos |
|
|
|
|
Генераторатор |
Ux(t) |
|
|
|
U(t) |
U x2 (t) U y2 (t) |
|||||
ма |
Vx(t) |
|
|
|
|
шума |
|
|
|
|
|
ГеГенератортор |
Uy(t) |
arctg[Uy(t)/Ux(t)] |
(t) |
||
а |
Vy(t) |
|
|||
sin 0ti |
|
||||
шума |
|
||||
|
Asin |
|
|
|
s(t) |
|
|
|
|
|
|
cos 0ti
Рис. 5. Структурая схема формирования огибающей, фазы
ивысокочастотного сигнала
7.2.2.Структура программы и задание на работу
ЛабораторнаяработавыполняетсянаПЭВМ. Онасостоитвсамосто-
ятельном выполнении заданий, которые расположены в семи фраг-
ментах(Ф.1–Ф.7) заданнойпрограммы, представленнойвп. 7.2.3. Впрограмме каждый фрагмент помечен зеленым цветом. Задание (в рамках конкретного фрагмента) предполагает внесение в программу отсутствующих операторов MathСad (в программе их места помечены желтым цветом) и выполнение необходимыхпозаданиючисленныхрасчетов.
Привыполнениизаданийиспользуйтеопыт, полученныйвлабораторной работе 1, исходную программу, структурную схему (рис. 5) и применяйтеудобныеобозначения (см. рис. 5).
При выполнении заданий не рекомендуется работать в режиме «Automatic Calculation». Изменениярежимаработыосуществляютсяпри вызовеменю «Math». Запуск программы в ручном режимепроизводитсянажатиемклавиши F9.
Всеуказанныенижезаданиявыполняютсядлязначенийпараметров: a 0; 2;10 и 60 ;170 . Желтым цветом в программе отмечены

194
операторы, которыеследует записать самостоятельно, исходяиз смысла вычислений.
Исходная программа состоит из следующих четырех разделов (блоков), началокоторыхотмеченосиним цветом.
1. Блок генерации двухстатистически независимых случайных последовательностей (выборок) квадратурных компонент смеси сигнала и гауссовского шума. Для этогодолжны быть заданы величины амплитуды, фазырегулярногосигналаисреднееквадратичноезначениешума .
Формирование двух независимых случайных последовательностей
Ux (Ux1,Ux2 ,...,Uxi ,...,UxN ) и Uy (Uy1,Uy2 ,...,Uyi ,...,UyN ) квадра-
турных составляющихпроисходит придвукратном обращениик процедуре rnorm(N,0, ). Для просмотра полученных последовательностей в блоке осуществляется вывод двух графиков.
Выполняя задание, образуйте в программе последовательности Ux и Uy призаданныхзначенияхпараметров a и . Следуетобратитьвниманиенасредниезначенияквадратур. Онидолжныиметьзначения, равные соответствующим параметрам в формуле для ПРВ (17). Для удобствавосприятияграфиковследуетзадаватьобъемвыборки N 200…400.
2.Блоквычисления выборочныхзначений огибающейи фазывысокочастотногосигнала (10). Длявычислениявыборочныхзначенийфазы используйтевстроеннуюфункциюatan2(Ux,Uy), котораявычисляетфазу (в радианах) в интервале [– ; ]. Для просмотра огибающей и фазы вблокепроизводится выводграфиководиночныхреализаций, приэтом используетсятиплинийдляграфикаlines.
Выполняязадание, определитетеоретическиезначенияматематическихожиданийогибающейифазырадиосигналапризаданныхвеличинах параметров (см. подразд. 2.3). Изучитехарактервариаций фазы при различных (малых и больших) величинах параметра а и разных величинах — всерединеинаграницеинтервалаоднозначности. Объяснитехарактеризмененийфазы.
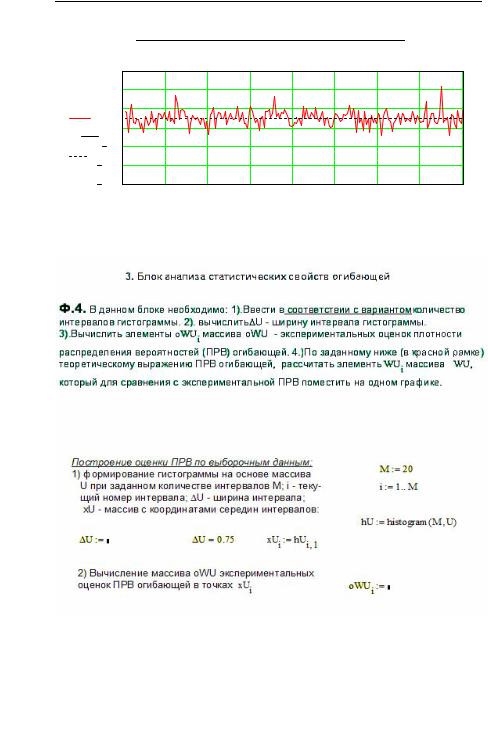
3.Блоканализастатистическихсвойств огибающей. Вблокевычис-
ляются: mU — оценка математического ожидания огибающей (в программеиспользованообозначение«omU»); U — оценкасреднегоквадратичногозначенияогибающей(впрограммеиспользованообозначение «o U»); W (U ) — оценка ПРВ огибающей (в программе использовано обозначение«oWU»).
Выполняязадание, сравнитевыборочныезначенияоценокссоответствующимитеоретическими (среднимипоансамблю) значениямипараметров и ПРВ (п. 2.3.1).

195
Значение модифицированной функции Бесселя нулевого порядка I0 (UA/ 2 ) , котораявходитввыражениеПРВ W(U), следуетвычислить спомощьювстроеннойвMathСad функции I0( ) . Ееможнонайтипосле вызова «f(x)» в разделе «Function Category», выбрав строку «Bessel»,
и далее в разделе «Function Name», выбрав строку «I0». При вычисленииоценкиПРВнеобходимоиспользоватьпроцедуруhistogram(·) иопыт ееприменениявлабораторнойработе1.
4. Блоканализастатистическихсвойствфазы. Вблокевычисляются:
m — оценка математическогоожиданияфазы (в программеиспользовано обозначение «oma»); — оценка среднего квадратичного значенияфазы(впрограммеиспользованообозначение«o »); W ( ) — оцен- ка ПРВ фазы (в программеиспользовано обозначение «oW »).
Выборочные оценки, полученные в данном блоке программы при различныхзначенияхпараметров a и , сравнитестеоретическимизначениямипараметров иПРВ (см. п. 2.3.2). Объяснитевидтеоретической ПРВ фазы при значениях 60°; 170°; а 3.
Значение интеграла вероятности Ф(x), который входит в выражение ПРВ W( ), следуетвычислить спомощью встроенной в MathСad функции pnorm(x,0,1). Ееможнонайтипослевызова«f(x)» вразделе«Function Category», выбравстроку«All», идалеевразделе«Function Name», выб-
рав строку «pnorm». При вычислении оценки ПРВ необходимо использоватьпроцедуруhistogram(·) иопытееприменениявработе1. Пункт3 и 4 выполнять для значений а 0; 2; 10. Объем выборки N задавайте 500–1000 при числе разрядов гистограммы 20–40.
5. Блокформированиядискретныхзначений sn s(tn ) радиосигнала s(t) (рис. 5). Представим (9) в дискретной форме
s(tn ) sn Acos Vn cos n cos(2 n |
t |
) |
|
|||
|
|
|||||
|
|
|
|
T0 |
|
|
|
|
t |
|
|||
[Asin Vn sin n |
]sin 2 n |
|
, |
(18) |
||
|
||||||
|
|
T0 |
|
|||
где n 1,2,..., N — номер дискретного отсчета (N — объем выборки);
t — отношениеинтерваладискретизациик периодувысокойчастоты
T0
(положитьравным 0,5–0,125). Изучитеповедениефункции s(tn ) . Количествоотсчетовприпостроенииграфикафункции (18) задайте100–400. Длявыводаграфикаиспользуйтетиплинииlines.

196
6.Выполните экспериментально расчет зависимости оценки СКО фазы от величины параметра a для значений a 0;1; 3;10; 50. Фазу регулярногосигнала положитеравной нулю.
7.Полагая 60°, выполните в программе формирование оценки фазыполезногосигнала повыборкеиз5 временныхотсчетовфазы смесисигналаишумапри A / 2 . Каковатеоретическаяточность(СКО) этойоценки? Отчегооназависит? Рассчитайтееетеоретическоезначение
иопределите объем выборки для достижения СКО оценки фазы 1 градус. Проверьтеэкспериментальнополученныйрезультат.
По итогам работы сделайте выводы. Отчет по работе представьте ввиделистингапрограммысвыполненнымифрагментамиивыводами.
7.2.3. Листинг программы в среде MathCad

197
198 |
|
|
|
|
|
|
|
|
|
|
|
Одиночная реализация фазы смесисигнала и шума |
|
|
|||||
|
180 |
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
n |
60 |
|
|
|
|
|
|
|
|
180 |
0 |
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
180 |
25 |
50 |
75 |
100 |
125 |
150 |
175 |
200 |
|
0 |
||||||||
|
|
|
|
|
n |
|
|
|
|

199

200
