
Статистические методы обработки сигналов в радиотехнических системах
..pdf
11
|
|
y(t) s(t, , ) n(t), |
|
||
Acos (t ) , |
0 t и |
T , |
|||
где s(t, , ) |
0, |
t , |
( и ) |
t. |
|
|
|
||||
Здесь полезный сигнал зависит от пяти параметров: амплитуды А, частоты , начальнойфазы , длительностиимпульса и имоментаего появления . Впрактическихзадачахчастоинформативнымиинеизвестными заранее могут быть 1 ; 2 ; 3 и , а мешающими —
1 A и 2 .
При радиолокационном наблюдении объекта, находящегося впространстве, содержащемслучайныенеоднородности(самолетидождевыеоблаканатрассераспространениярадиоволниликорабльивзволнованная поверхность моря), также возникает помеха в виде радиосигналов, отраженных от капель дождя или случайно ориентированных участковповерхности моря. Однаковэтомслучаепомеха несуммирует-
сяс сигналомот объекта, онамодулируетполезный сигнал, тоесть вли- яетнанего нелинейно. Такиепомехи называют мультипликативными,
(от английского слова multiply — умножать). Действительно, простое увеличениемощностиизлученногосигналаприведеткослаблениювлияния собственного шума в случае аддитивной помехи и не приведет к желаемому результату в случае мультипликативной помехи, так как нарядус увеличением уровня сигнала, отраженногоот объекта, возрастети уровеньпомехи ввидеотражений отоблаков или моря.
Математическоеописаниепомехипредполагаетзаданиеееввидеслучайнойфункциивремени. Впротивномслучае(придетерминированном описании) она оказывается полностью известной, и ее влияние можно полностью исключить. Вопрос отом, является ли отдельновзятый процесс сигналом или помехой, решается в зависимости от конкретной задачи. Вэтомпланематематическиеспособыописаниясообщений, сигналов или помех одинаковы. Поэтому далее, где это удобно, будет использоватьсяединыйтермин«сигнал».
Важноотметить, чтона вход приемника поступает результирующий сигнал y(t, (t), ) ипосвоейфизической природевподавляющембольшинствепрактическихзадач— этослучайныйпроцесс. Такимобразом, амплитуда, фаза и частота высокочастотного (ВЧ) сигнала y(t, (t), ) в любой момент времени являются случайными величинами. Напомним, что определение случайной величины или случайного процесса как совокупности случайныхвеличин предполагает задание некоторого

12
множества возможных значений (выборочного пространства), из которогопроизводитсяслучайныйвыборконкретных(наблюдаемых) реали- заций. На этом множестведолжны быть определенывероятностные характеристики, которыепоказывают, какчастонаблюдаютсятеили иные элементывыборочногопространства.
Важнымположениемтеорийинформацииисвязиявляетсяутверждение, что адекватная (полноценная или соответствующая природе явлений) постановказадачианализаисинтезаРТСпередачиилиизвлечения информации предполагает задание полезного сообщения (t) как случайнойфункциииливеличины, если (t) const. Действительно, предположение о том, что сообщение (t) является детерминированной функцией, те. . известнойпотребителюзаранее, делаетабсурднойпередачу этого сообщения по каналу связи. Теряет смысл и задача измерения координатвРЛ- иРН-системах, еслионизаранееизвестны, тоестьявляются детерминированными функциями, определяющими изменение самихкоординат.
Такимобразом, общий подходкматематическомуописаниювоздействийвРТСразличногоназначения, аследовательно, икрешениюзадач анализа и синтеза систем и устройств обработки сигналов связан с использованием аппарата статистической радиотехники. Тем не менее, отсюда не следует, что теряет смысл изучение свойств переносчика информации— сигнала s(t, (t), ) — приотсутствиипомех. Вчастности, особыйинтереспредставляетизучениевлиянияспособамодуляциисигнала навозможностьраздельногонаблюдениядвухсигналов, имеющих различныезначениясообщений 1(t) и 2 (t) . Уверенностьвцелесообразности подобногорассмотрения основана на том, чтосвойства сигналов, справедливые при отсутствии помех, сохранятся на приемлемом уровне при достаточном превышении сигнала над помехой. Далее мы покажем, чтоэтоимеет местов задачах, где помехой является собственныйшумприемника.
1.2. Классификация сообщений и сигналов
Рассматриваяклассификациюсообщенийисигналов, будемполагать, чтоони не являются функциями пространственных координат и в качествеаргумента могутиметьпеременную t (время).
Напомним, чтопосвоейсутисообщениедолжнорассматриватьсякак категория, заранее неизвестная получателю. В этом смысле сообщение неможетбытьдетерминированным, те. . заведомоизвестнымпотребите-
13
лю. РольпоследнеговРТСпередачиинформациивыполняет, например, абонентнаприемномконцелиниисвязи. ВРТСизвлеченияинформации этоможетбытьоператорРЛС, получающийинформациюокоординатах целей в зоне обзора.
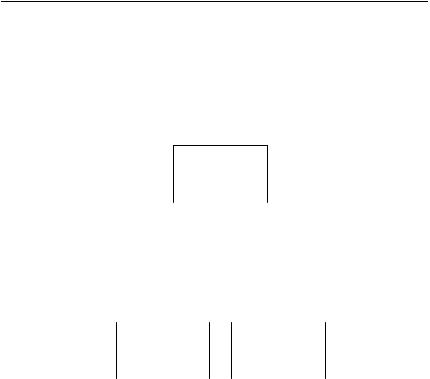
Классификациясообщений представлена на рис. 1.1. Взависимости от характера изменения функции (t) во времени сообщения бывают
случайные и квазидетерминированные.
Полезное
сообщение
(t)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Случайная |
|
|
Квазидетерми- |
|
|
Постоянная |
||||||||
|
|
нированная |
|
|
неслучайная |
|||||||||
функция |
|
|
|
|
||||||||||
|
|
функция |
|
|
величина |
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналоговая (непрерывная по уровню)
Цифровая (дискретная по уровню)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дискретная |
|
Непрерывный |
|
|
Непрерывный |
|
|
Дискретная |
||||
последова- |
|
во времени |
|
|
во времени |
|
|
последова- |
||||
тельность |
|
процесс |
|
|
процесс |
|
|
тельность |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.1. Классификация типов сообщений (t)
Сообщениеявляется случайнойфункцией, еслионопредставляетсобойпоследовательностьслучайныхвеличин, тоестьвлюбойпроизвольный момент времени, где оносуществует, егоможно рассматривать как случайнуювеличину. Согласно[1] — этотакойпроцесс, вкотором«случайностьрождаетсявкаждый моментвремени». Статистическоеописание случайной функции в общем случае предполагает задание многомернойплотностираспределениявероятностей(ПРВ) значенийсообщения(t) в n моментоввремени t1, ,tn . Есливвестиврассмотрениеn-мер- ный вектор ( 1, 2 , , n ) с координатами i (ti ) , то следует

14
задать функцию W( ; t1,t2 , ,tn ) W( 1, 2 , , n ; t1,t2 , ,tn ). Здесь множествомоментоввремени ti играетрольпараметровфункции. Если
моменты времени t1, ,tn расположены равномерно через промежуток t в интервале [0, T], на котором задан случайный процесс, то ПРВ W( ) при большом n можно приблизительно рассматривать как плотностьвероятностидляреализациислучайногопроцесса. При t 0 число отсчетов n и n-мерная ПРВ в пределе (если он определен) переходитвфункционалраспределениявероятностей W{ (t)} случайного процесса (t).
Во многих практических задачах оказывается достаточным знание одноилидвумерной ПРВ. Этопозволяетзадатьматематическоеожидание(среднеепоансамблюреализацийзначение)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
W ;t d |
|
|
|
|
|
|
||||||||
|
|
|
|
|
M |
t t |
|
|
|
|
|
|
|
||||||||||||
иковариационнуюфункцию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
(t ,t |
2 |
) M |
|
|
|
2 |
|
|
|
2 |
W ( , |
2 |
;t ,t |
2 |
) d d |
2 |
. |
||||||
|
1 |
1 |
|
1 |
|
|
|
|
1 |
|
1 |
1 |
1 |
|
|||||||||||
Втех случаях, когда необходимознание n-мерной плотности вероятности, часто в качестве моделей для описания случайных сигналов и помехиспользуются процессы, укоторыхмногомерная плотность можетбытьопределеначерезодноилидвумернуюплотностьвероятности. Вчастности, еслимоментывремени ti выбранытак, чтосоответствующие им значения 1, 2 , , i , n оказываются статистически независимыми, то n-мерная плотность выражается через произведение одномерных, те. .
Wn ( 1,..., n ;t1,...,tn ) W1( 1,t1) W1( 2 ,t2 ) W1( n ,tn ).
Всилуизвестнойвтеориивероятностейцентральнойпредельнойтеоремы во многих задачах, связанных с анализом и синтезом устройств обработки сигналов, применяетсявероятностнаямодель, соответствующая нормальному (гауссовскому) случайномупроцессу. Онаудобна тем, что n-мернаяПРВ полностьюопределяется черездвумерную плотность распределения вероятностей значений процесса (t1) , (t2 ) для произ-
вольных t1 и t2 . ШирокоеприменениевтеорииРТСнаходятудобныеипростыемоде-
ли случайных сигналов, которые строятся на основе так называемых

15
случайных процессов без последействия, или процессовМаркова. Случайный процесс (t) называется марковским (первого порядка), если условная плотность вероятности процесса n в момент времени tn по всем предыдущим значениям n 1, n 2 , , 1 зависит только от n 1 ,
то есть W ( n / n 1, n 2 , , 1) W ( n / n 1) . Для марковского процесса n-мернаяплотностьвероятностиможетбытьзаписанаввиде
W ( 1, 2 ,..., n ) W ( 1) W ( 2 / 1) W ( 3 / 2 ) W ( n / n 1),
тоестьонаопределена, еслиизвестнаПРВначальногозначенияпроцесса1 (t1) и условная ПРВ W( i/ i–1), называемая плотностью вероят-
ностиперехода.
Сообщение является квазидетерминированным, если его задание представляет известную функцию времени t, содержащую один или несколькослучайныхпараметров, 1, 2 , , m . Например, математическуюмодельизменениякоординатыцели, допустимдальности D(t), на интервалевремени (0;T ) определяютввидеполинома
D(t) a0 a1t a2t2,
тогда a0 ,a1,a2 . Очевидно, этодопустимо, есливозможнопренебречьслучайнымивовременивариациямидальностиисчитатьускорение постояннымнаинтерваленаблюдения.
Ясно, чтоисчерпывающее описание ансамбля сообщений (t) вданномслучаевозможнопри заданиимногомерной плотностивероятности W 1, 2 ,..., m . Частным случаем квазидетерминированного сообщения является константа — случайная величина, которая постоянна на интервале наблюдения. Такая модель сообщения определена заданием ПРВ W( ), она достаточно проста и удобна для описания реальных сообщений, которые «мало» и «медленно» изменяются на интервале наблюдения.
Достаточно часто в практических задачах рассматривают сообще-
ниекак неизвестнуюпостояннуюинеслучайнуювеличину илисистему не случайных величин. В задачах такого типа нет необходимости вводить в рассмотрение плотность распределения вероятностей W( . Данный подход оправдан, если есть уверенность в том, что априорное знаниефункции W( , тоестьеезнаниедополучениясигнала y(t; 0 ), содержащего информацию о конкретном истинном значении сообщения 0 , практически ничего не может дать потребителю. Он также

16
оправдан ивтомслучае, когда сообщениепосвоейфизической природе неможетрассматриватьсякакслучайное. Например, вкачествесообщениявизмерительнойРТСможетвыступатьнеизвестнаяфизическаяконстанта — скорость света, и если ее предстоит измерить, то следует рассматриватькакнеслучайнуювеличину.
В качестве второго признака классификации будем использовать характермножествазначенийфункции (t) иееаргумента t. Взависимости от непрерывного или дискретного множества значений функции(t) различают аналоговые и цифровые сообщения. В каждом из этих вариантов множество значений переменной t может быть дискретным илинепрерывным. Витогеполучаемчетыреосновныхтипасообщений:
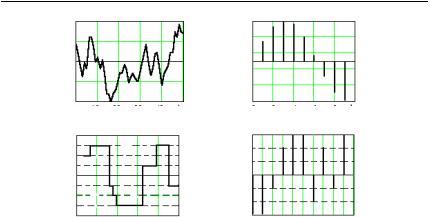
1)непрерывный случайный процесс — процесс (сигнал), область значений и область определения которого непрерывные множества
(рис. 1.2,а);
2)непрерывный процесс с дискретным временем — процесс,
укоторогообластьзначений непрерывноемножество, а область определения — дискретное. Сообщения такого типа образуются в результате формированиявременныхвыборок(дискретныхотсчетов) изнепрерывного случайного процесса (рис. 1.2,б);
3)дискретныйслучайныйпроцесс(дискретныйпроцессснепрерыв-
нымвременем) — процесс, укоторогообластьзначенийдискретноемножество, аобластьзначенийаргумента t — непрерывноемножество. Этот процессобразуетсяврезультатеквантованиянепрерывногопроцессатолько по уровню (рис. 1.2,в);
4)дискретнаяслучайнаяпоследовательность(дискретныйпроцесс
сдискретным временем) — процесс, у которого область значений сообщения и область определения аргумента t — дискретные множества (рис. 1.2,г). Сигналыподобноговида широкоиспользуютсяв современныхРТСразличногоназначения, реализующихдискретныеицифровые методыобработкиинформации.
Рассмотримклассификациюсигналов-переносчиковсообщенийвРТС (рис. 1.3). Высокочастотный (ВЧ) сигнал, не содержащий сообщение(t) — немодулированное гармоническое колебание (несущаябез модуляции), имеетвид
s(t) S0 cos( 0t 0 ), |
(1.1) |
где S0 , 0 , 0 — амплитуда, частотаиначальнаяфазаколебания.
17
(t) |
(k) |
|
6 |
0,6 |
|
0,2 |
||
0 |
||
–0,2 |
||
–6 |
||
–0,6 |
||
–12 |
||
–1 |
||
0 10 20 30 40 t |
0 2 4 6 8 k |
|
а |
б |
|
(t) |
(k) |
|
2 |
0,67 |
|
1 |
0,33 |
|
0 |
0 |
|
–1 |
–0,33 |
|
–2 |
–0,67 |
|
–3 |
–1 |
|
–4 |
||
0 2 4 6 8 t |
0 1 2 3 4 5 6 7 8 k |
|
в |
г |
Рис. 1.2. Одиночные реализации различных типов сообщений
Сигнал, содержащий сообщение, в общем случае можно записать в виде
s(t) S(t, (t))cos( 0t Ф(t, (t)) 0 ), t 0,T , |
(1.2) |
где S(t, (t)) и Ф(t, (t)) — функции, определяющие амплитудную и фазовую модуляцию ВЧ-сигнала сообщением (t); T — длительность сигнала(времянаблюдения), котораявреальныхзадачахконечна. КонкретныйвидэтихфункцийзависитотназначенияРТСиспособаеепостроения.
При проектировании устройств обработки сигналов во всех типах РТС существенное значение имеет характер высокочастотной струк- турысигнала s(t, (t)). Поэтомупризнакувсесигналыможноразделить на два типа: когерентные и частично когерентные, включая в них иполностьюнекогерентные. Укогерентныхсигналовизменениевовремениихфазыполностьюизвестно, тоестьописываетсядетерминированной функцией. Это позволяет, например, производить компенсацию нежелательных фазовых сдвигов и осуществлять, в частности, синфазное сложение нескольких ВЧ-сигналов. В итоге можно увеличить мощность суммарного сигнала. Когерентное суммирование (накопление) часто используется в устройствах оптимального приема сигналов при наличии помех. В случаечастичнокогерентныхсигналов ВЧ-структура вопределенной степени случайна. Такимобразом, их сложениенеприведетканалогичномурезультату.

18
Переносчик
информации ВЧ-сигнал s(t, (t))
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Повысокочастотной структуре |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Случайные |
|
|
|
Детерминиро- |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
функции |
|
|
|
|
|
ванные |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
(частично |
|
|
|
|
функции |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
когерентные) |
|
|
|
(когерентные) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По числу ступенеймодуляции |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сигналы с |
|
Сигналы с 2 и |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
одноступенча- |
|
болееступенями |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
той модуляцией |
|
|
модуляции |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По типусигнала поднесущей |
|
|
|
|
|
|
|
|||||||||||||||
|
Сигналы |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
с модуляцией |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
несущей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Регулярная импульсная |
|
|
|
Непрерывная |
|
|
|
||||||||||||||||||||||||||||
|
(АМ, ФМ, ЧМ) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
последовательность |
|
|
|
поднесущая |
|
|
|
|||||||||||||||||||
|
Вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
модуляции |
АИМ |
|
|
ВИМ |
|
|
ШИМ |
|
КИМ |
|
|
|
АМ |
|
|
ЧМ |
|
ФМ |
|
|||||||||||||||||||
в 1-й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ступени |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
модуляции |
|
|
АМ,ЧМ |
АМн |
|
|
ЧМн |
|
ФМн, |
|
АМ |
|
|
ЧМ |
ФМ |
|||||||||||||||||||||||
во 2-й |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОФМн |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ступени |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 1.3. Классификация сигналов-переносчиков сообщений
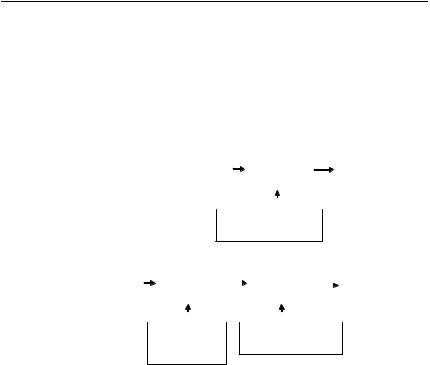
Взависимости от количестваступеней модуляции модулированные колебания s(t, (t)) могутбытьдвухтипов: соднойступеньюмодуляции
ис двумя и более. На рис. 1.4 показана структурная модель формирования переносчика сообщения s(t, (t)) для обоих способов.
Вслучае одной ступени модуляции несущего колебания (1.1) сообщение (t) непосредственно изменяет параметр радиосигнала. Различают амплитудную модуляцию (АМ), частотную модуляцию (ЧМ)
19
и фазовую модуляцию (ФМ) (рис. 1.4,а). Например, сигнал в системах радиовещаниясЧМможнопредставитьввиде
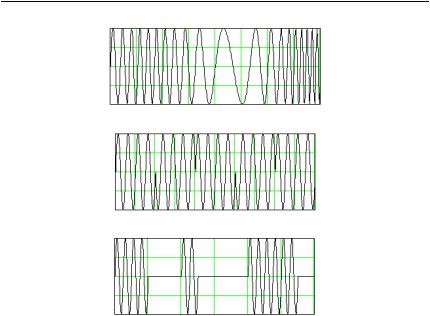
s(t, (t)) S0 cos 0t (t) 0 ,
где скорость изменения полной фазы, те. . мгновенная частота, должна быть равной (t) 0 (t) 0 k (t) при k const.
Источник |
|
Первая |
|
|
||
полезного |
|
ступень |
|
s(t, (t)) |
||
|
|
|||||
сообщения (t) |
|
модуляции |
|
|||
|
|
|
|
|
|
|
Не модулированная
анесущая s(t)
Источник |
|
|
Первая |
|
|
|
Вторая |
|
|
|
|
||
полезного |
|
|
ступень |
|
|
|
ступень |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
сообщения |
|
|
модуляции |
|
|
|
модуляции |
|
s(t, (t)) |
||||
(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Источник |
|
|
Не модулированная |
|||||||
|
|
|
поднесущего |
|
|
|
несущая s(t) |
|
|
|
|||
бсигнала П(t)
Рис. 1.4. Структурная модель формирования сигнала-переносчика информации: а — одна ступень модуляции; б — две ступени модуляции
Образец подобного сигнала показан на рис. 1.5,а. В РН-системах наземный маякснепрерывнымизлучениемсоздаетнавходеподвижно-
го бортового приемника сигнал s(t, (t)) k cos 0 t (t) / c 0 , где k — коэффициент, учитывающий ослабление волны на трассе рас-
пространения; с — скорость света; (t) — сообщение, определяемое изменением дальности D(t) от передатчика (маяка) до подвижного объекта.
Сигналы с несколькими ступенями модуляции широко применяются в современных системах связи, радиолокации и радионавигации. Они имеют более сложную структуру. В частности, при 2-ступенчатой модуляции существуют два модулятора. В первой ступени происходит модуляцияподнесущегосигнала П(t), вовторой — модуляциянесущего сигнала s(t) (рис. 1.4,б).
20
s(t)
0
а
–1
12,5 25 37,5 50 62,5 75 87,5 t
s(t)
0 |
б |
|
–1
0 10 20 30 40 50 60 70 80 90 t
s(t) |
|
|
|
|
|
|
0 |
|
|
|
|
|
в |
–1 |
|
|
|
|
|
|
0 |
20 |
40 |
60 |
80 |
100 |
t |
Рис. 1.5. Виды модуляции
ВЧ-сигнал s(t, (t)) может иметьподнесущую П(t) двух типов: регулярнаяпоследовательностьимпульсов; непрерывнаяфункция.
При использовании в качестве П(t) регулярной (периодической) последовательности импульсов определенной формы возможны четыре основныхвидаимпульсноймодуляциивпервойступени:
амплитудно-импульснаямодуляция (АИМ) — сообщение (t) изменяетамплитудуимпульсов;
время-импульсная модуляция (ВИМ) — сообщение (t) изменяет временноеположениеимпульсовотносительноопорной(немодулированной) последовательности;
широтно-импульсная модуляция (ШИМ), при которой сообщение управляет шириной (длительностью) импульсов, образующих поднесущуюП(t);
кодово-импульсная модуляция (КИМ), при которой по существу не происходит (в привычном смысле) модуляции какого-либо параметра импульсной последовательности П(t). Поясним подробнее этот вид модуляции.
