
Радиоматериалы и радиокомпоненты
..pdf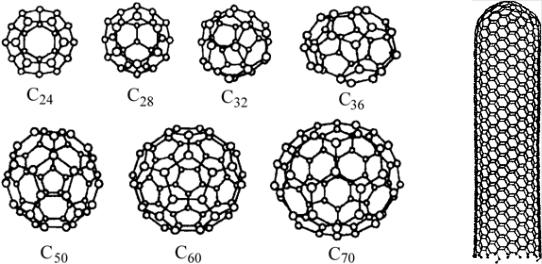
а) |
б) |
Рисунок 1.11 Примеры углеродных наноструктур: некоторые фуллерены (а) и углеродная нанотрубка (б).
В настоящее время значительный интерес вызывают наноразмерные структуры, сформированные из различных полупроводниковых материалов, в частности нитевидные нанокристаллы из кремния, арсенида галлия и др. Примером встроенных наноструктур являются полупроводниковые гетероструктуры, представляющие так называемые квантовые точки и ямы.
Сейчас трудно прогнозировать все возможные применения, которые найдут наноструктуры. Даже если отвлечься от разнообразных применений в медицине, энергетике, вычислительной техники и других отраслях науки и техники, эти структуры, несомненно, окажут значительное влияние на ассортимент новых электро- и радиоматериалов.
21
2 ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА ПРОВОДНИКОВЫХ МАТЕРИАЛОВ
2.1 Зонная энергетическая структура металлов
Чтобы понять, почему металлы обладают значительной проводимостью, намного большей, чем проводимость диэлектриков и полупроводников, следует рассмотреть, хотя бы на элементарном уровне, какова структура их энергетических зон.
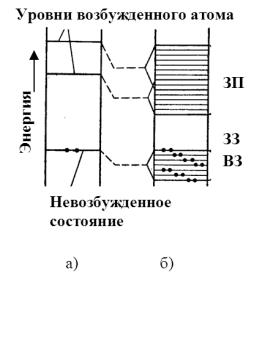
В изолированном атоме имеется ряд разрешенных уровней энергии, которые могут быть заселены электронами (рис 2.1, а). Если атомов много, но они удалены на достаточно большие расстояния друг от друга, структура энергетических уровней не изменяется, а электроны по-прежнему оказываются локализованными вблизи своих ядер. При конденсации вещества и при образовании кристаллической решетки твердого тела все имеющиеся у атомов данного типа электронные уровни (как заполненные электронами, так и незаполненные) несколько смещаются вследствие действия соседних атомов друг на друга. Притяжение электронов одного атома ядром соседнего снижает высоту потенциального барьера, разделяющего электроны в уединенных атомах, что приводит к перекры-
тию электронных оболочек. Благодаря перекрытию оболочек электроны могут без изменения энергии, посредством обмена, переходить от одного атома к другому, то есть перемещаться по кристаллу. Обменное взаимодействие имеет чисто квантовую природу и является следствием неразличимости электронов. В этом случае уже нельзя говорить о строгой принадлежности того или иного электрона определенному атому, то есть происходит обобществление электронов.
Вследствие обменного взаимодействия дискретные энергетические уровни изолированного атома расщепляются в энергетические зоны (рисунок 2.1, б). Разрешенные энергетические зоны разделены запрещенными интервалами энергии - запрещенными зонами (на рисунке - ЗЗ). Уровни энергии внутренних оболочек, которые локализованы вблизи ядра и не подвержены сильному возмущению со стороны окружающих атомов, расщепляются меньше, чем уровни валентных (внешних) электронов.
Рассмотрим простую кристаллическую решетку, образованную одним сортом атомов. В каждой разрешенной энергетической зоне содержится квантовых состояний в количестве, соизмеримом с количеством атомов во всем кристалле. Если учесть, что энергетические зоны имеют ширину порядка единиц эВ, то для
22
кристалла размером 1 см3, содержащего 1022 − 1023 атомов, энергетическое “расстояние” между уровнями окажется ~ 10−22 − 10−23 эВ. Эти цифры говорят о том, что энергетический спектр зоны можно считать непрерывным, поскольку даже тепловые флуктуации энергии электрона при нормальных условиях составляют значительно большую величину, ~ 10−3 эВ.
Стремление системы частиц к минимуму энергии приводит к тому, что энергетические уровни зон заселяются имеющимися электронами "снизу вверх". При этом действует принцип Паули – каждый уровень может быть заселен не более чем двумя электронами с противоположно ориентированными спинами. В итоге, нижние зоны заселяются полностью вплоть до зоны, образованной валентными уровнями. Валентная зона (на рисунке - ВЗ) является последней заселяемой зоной. В зависимости от "укомплектованности" электронами она может оказаться либо полностью заполненной, либо частично заполненной. Например, если валентная зона образована S - оболочками атомов, имеющих по одному электрону (щелочные металлы), то она будет заполнена ровно наполовину. Следующая за валентной зоной свободная, незаполненная электронами зона называется зоной проводимости (на рисунке -ЗП). Взаимное положение этих зон и степень заполнения валентной зоны определяют большинство процессов, происходящих в твердом теле.
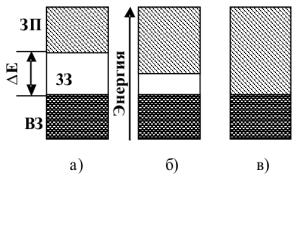
1. Предположим, что валентная зона заселена полностью (рисунок 2.2). Если при этом между валентной зоной и зоной проводимости имеется доста-
точно большая запрещенная зона E >~ 0.1 эВ, то такое состояние соответ-
ствует |
либо |
полупроводнику |
( E 3 эВ), |
либо |
диэлектрику |
( E ≥ 3 эВ). |
Находясь в валентной |
|
зоне, электроны совершают квантовомеханические движения, но не способны к направленному движению (дрейфу) в электрическом поле, поскольку для этого им необходимо из-
менять свою энергию, переходя с уровня на уровень. Но если уровни энергии в пределах валентной зоны полностью заселены, дрейф возможен лишь при условии перебрасывания части электронов из валентной зоны в зону проводимости за счет внешних возбуждающих факторов (температурный нагрев, освещение и т.д.).
2. Случай, когда запрещенная зона оказывается сильно узкой (<< 0.1 эВ), или вовсе отсутствует (валентная зона перекрывается с зоной проводимости), соответствует материалу с высокой проводимостью − металлу. В этом случае электроны, находящиеся на границе заселенности имеют возможность относительно свободно изменять свою энергию при воздействии внешнего электрического поля, беспрепятственно переходя с одного энергетического уровня на другой.
23

3. Если валентная зона заселена электронами частично то, очевидно, что соответствующий материал обладает металлическими свойствами независимо от взаимного расположения зон.
Случай перекрытых зон и случай частично заполненной валентной зоны с точки зрения электропроводности эквивалентны. Важно отметить, что концентрацию носителей заряда ("свободных" электронов, участвующих в электропереносе) можно считать почти постоянной по отношению к изменению внешних условий. Это свойство отличает металлы от полупроводников, у которых количество носителей заряда резко возрастает с ростом температуры.
2.2 Основные электрические параметры металлов
Из общего курса физики известно, что плотность электрического тока в веществе определяется зарядом q, концентрацией n и дрейфовой (средней направленной) скоростью носителей заряда vдр
j = q n vдр. |
(2.1) |
Дрейфовая скорость определяется как средняя векторная сумма скоростей электронов. Дрейфовую скорость нельзя путать с тепловой скоростью vT, кото-
рая равна среднему модулю скорости отдельных электронов:
|
|
|
v i |
|
v |
|
= |
i |
|
др |
n |
|||
|
|
|||
|
|
|
;
|
i |
|
|v | |
v |
= i |
T |
n |
|
.
(2.2)
Средняя тепловая скорость связана с температурой металла соотношением mvТ 2 = 3 kT, откуда следует, что при комнатной температуре ~300 К, теп-
ловая скорость значительна и имеет порядок 105 м/с.
В силу того, что направления скоростей электронов хаотичны, в отсутствие электрического поля дрейфовая скорость равна нулю. При воздействии электрического поля скорости электронов получают некоторую добавочную составляющую против направления напряженности поля. Однако эта добавка незначительна, и практически не влияет на характер теплового движения электронов. Элементарные расчеты показывают, что при самом жестком режиме протекания тока в металле величина дрейфовой скорости составляет не более ~10-4 м/с, то есть на 9 и более порядков меньше тепловой. Это связано с тем, что электроны, приобретая от внешнего поля незначительный избыток энергии (сверх тепловой энергии), тут же рассеивают его в материале в результате взаимодействия с динамическими и статическими дефектами кристалла. В условиях столь больших сил "трения" имеет место прямая пропорциональность между дрейфовой скоростью и напряженностью поля:
24
vдр= E. |
(2.3) |
Коэффициент пропорциональности носит название “подвижность” [м2/В с]. Подстановка (2.3) в (2.1) дает выражение
j = q n E. |
(2.4) |
Коэффициент пропорциональности между плотностью тока и напряженностью поля носит название “удельная проводимость” [ ]=[1/Ом м], а величина,
обратная к нему - “удельное сопротивление” [ ]=[Ом м]:
= q n =1/( q n ). |
(2.5) |
2.3 Удельное сопротивление чистых металлов
Если бы кристаллическая решетка металла была лишена дефектов, электрическое сопротивление металла равнялось бы нулю, поскольку электроны не испытывали бы рассеяния энергии и беспрепятственно ускорялись в электрическом поле. При этом неподвижные собственные ионы, расположенные в регулярных узлах кристаллической решетки, не являются рассеивающими центрами,
всилу самосогласованности их полей с квантово-механическим движением электронов.
На самом же деле, как отмечалось ранее, присутствие дефектов структуры в кристаллической решетке неизбежно. Рассеяние электронов может произойти и
врегулярных частях кристалла, поскольку строгая периодичность его нарушается тепловыми колебаниями ионов. Опыт показывает, что именно тепловые ко-
лебания решетки являются главным рассеивающим фактором в чистых метал-
лах. Отсюда следует, что с увеличением температуры сопротивление металлов должно монотонно расти, что и наблюдается в опытах. Рассмотрим типичную зависимость удельного сопротивления чистого металла от температуры (рисунок 2.3, а). Для большинства чистых металлов в области низких температур наблюдается ускоренный рост удельного сопротивления в зависимости от температуры, которую можно описать степенной зависимостью. В области относительно
высоких температур, выше так называемой температуры Дебая ТД, зависимость становится близкой к линейной зависимости. Характер роста удельного сопротивления на всем диапазоне температур можно объяснить лишь с позиций квантовой теории. Дело в том, что всякое колебание кристаллической решетки можно разложить на элементарные колебания, или колебательные кванты - фононы. Фононы, также как и электроны, обладают дискретным спектром энергий, причем разрешенная зона фононов имеет ширину ~0,01 эВ. Однако на фононы не распространяется принцип Паули, и каждому уровню энергии может соответствовать сколь угодно большое число фононов. Говоря упрощенно, при возрастании температуры от абсолютного нуля до температуры Дебая, увеличивается
25

количество фононов, соответствующее каждому отдельному возбужденному уровню энергии. Но, кроме того, возбуждаются все более и более высокие уровни энергии фононов. При температуре Дебая возбуждены уже все фононные уровни, поэтому прирост фононов замедляется и зависимость (T) переходит в линейную зависимость. Как показывает эксперимент, линейная аппроксимация температурной зависимости (T) справедлива для температур выше 2/3ТД с ошибкой, не превышающей 10%. Температура Дебая для большинства металлов составляет 400-450 К, поэтому линейное приближение обычно справедливо для температур от комнатной и выше.
Вблизи температуры плавления Тпл происходит отклонение от линейного закона, а при температуре плавления происходит резкий скачок удельного сопротивления, связанный с фазовым переходом (рисунок 2.3, а). Как правило, сопротивление расплава выше, чем сопротивление твердого металла. Исключение составляют такие металлы, как Bi, Ga и др, у которых при температуре плавления сопротивление падает.

|
|
|
|
|
|
ост |
|
|
|
|
|
0 |
T |
T |
д |
T |
T |
|
св |
|
пл |
|
/ 273
0,015
0,010
0,005
00 Тсв 10 15 Т,К
а) б)
Рисунок 2.3 - Температурная зависимость удельного сопротивления металлов: а − в широком диапазоне температур (схематично); б− в области низких температур для платины и ртути.
В области температур, близких к абсолютному нулю, некоторые металлы (например, Nb, Sn, Al, Zn, Hg и др.) переходят в сверхпроводящее состояние, при котором удельное сопротивление резко снижается до нуля (рисунок 2.3, б). У металлов, не переходящих в сверхпроводящее состояние (например, Pt, рисунок 2.3,б), при снижении температуры вплоть до нуля, удельное сопротивление остается на некотором постоянном уровне 0. Это значение называется остаточным сопротивлением. Очевидно, оно не связано с тепловым рассеянием электронов. Опыт показывает, что значение 0 пропорционально количеству примесей, и возрастает при закалке и механических деформациях. Следовательно, остаточное сопротивление связано только с наличием статических дефектов. Таким образом, удельное сопротивление металла можно представить в виде суммы температурозависимой и остаточной (постоянной по отношению к изменению температуры) составляющей.
26

= + . |
(2.6) |
Для количественного описания влияния температуры на сопротивление металлов на некотором ограниченном температурном диапазоне вводят понятие температурного коэффициента (ТК) удельного сопротивления.
Дадим вначале определение ТК произвольной температурозависимой величины А.
Температурным коэффициентом величины А называется относительное изменение величины А при изменении температуры на один градус:
TKA = |
1 dA |
= |
dln(A) |
|
1 ΔA |
|
|
A dT |
dT |
A ΔT |
|||||
|
|
|
|
1 A1
A2 T2
−A1
−T1
.
(2.7)
Первые два выражения тождественны и дают определение ТК для определенной температурной точки. Выражения, стоящие после приближенного равенства, дают определения ТК в конечных приращениях в окрестности некоторой температуры T1 на основе экспериментального измерения зависимости А(Т) в двух температурных точках T1 и T2. В соответствии с принятыми стандартами, относительное изменение величины определяют делением разности (А − А ) на значение, соответствующее наименьшей температуре диапазона А1. При слабой температурной зависимости величины А различия в приведенных формулах не имеют существенного значения.
Из (2.7) следует формула, позволяющая, на основе известного ТК и известного значения А при некоторой температуре T определить значение А при другой температуре Т:
А(Т) =А [1+ТКА (T−T ) |
(2.8) |
Независимо от величины А и ее размерности, температурные коэффици-
енты имеют одинаковую размерность – К −1.
Типичные значения температурного коэффициента удельного сопротив-
ления ТК для чистых металлов составляют ~10-3 К −1. Рассмотрим выражение для ТК металла с дефектами, используя выражение (2.7) и предполагая выполнение соотношения (2.6):
ТК =(1/ ) (d /dT) = 1/( + ) d /dT = ТК /( + ) |
(2.9) |
В полученном выражении учтено постоянство остаточного сопротивления (d /dT=0). Результат говорит о том, что при введении примесей (увеличении постоянной составляющей ) удельное сопротивление металла становится менее температурозависимым (ТК уменьшается). Опыт показывает, что
27
введением примесей это значение можно понизить на 1-2 порядка (при этом, однако, общее удельное сопротивление повышается).
Типичные значения удельного сопротивления чистых металлов составляют ~10-8 10-7Ом м, а типичные значения ТК составляют ~10-3 К −1.
Наиболее проводящими при комнатной температуре материалами является известная четверка металлов Ag, Au, Cu, Al. Их удельное сопротивление не превышает 3 10−8 Ом м.
2.4 Электрические свойства металлических сплавов
Наряду с чистыми металлами, на практике часто используют металлические сплавы. Получение сплава можно в некоторой степени считать введением примеси в металл, при котором концентрация атомов примеси соизмеряется с концентрацией основного вещества. При этом теряется смысл в разделении вещества на примесь и основу. Из сказанного следует, что удельное сопротивление сплава должно быть больше, чем удельное сопротивление отдельных компо-
нент, так как происходит взаимообусловленное нарушение периодичности кристаллических структур. В отличие от чистых металлов, остаточная составляющая удельного сопротивления сплава может во много раз превышать температурозависимую составляющую.
Для простоты рассмотрим сплавы, содержащие два компонента А и В. Для сплавов типа физического раствора температуронезависимая остаточная составляющая достаточно хорошо описывается параболической зависимостью Нортгейма:
= CXAXB CXB(1- XB), |
(2.10) |
где XA = NA /N и XB = NB /N – атомные доли компонентов А и В в сплаве; N, NA, NB – общая концентрация атомов и концентрации атомов А и В; C – константа, зависимая от природы компонент. Такая зависимость соответствует концентрационной зависимости полного удельного сопротивления, показанной на рисунке
2.4.
Сплавы имеют значительно более высокие значения удельного сопротивления, чем чистые металлы. С другой стороны, как следует, в частности, из выражения (2.9), сплавы более термостабильны, чем чистые металлы, то есть, их ТК ниже (рисунок 2.4). Оба этих свойства можно использовать для изготовления резисторов – проволочных и пленочных.
28
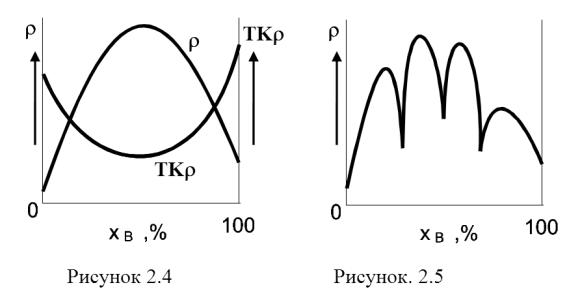
Закон Нортгейма хорошо выполняется лишь для сплавов типа физический раствор (смесь фаз). В ряде случаев, сплавы могут образовывать так называемые интерметаллические соединения - по сути, новые химические вещества со своей кристаллической структурой, в которой атомы двух компонент строго упорядочены. Например, в сплавах Mg − Zn могут образовываться такие соединения как MgZn, Mg2Zn3 , MgZn4 , MgZn6 с регулярными собственными кристаллическими решетками. На диаграммах “состав - удельное сопротивление” таких сплавов, на фоне общего максимума, при определенных соотношениях в составе, наблюдаются резкие провалы, соответствующие чистой интерметаллической фазе (рису-
нок 2.5).
2.5Влияние частоты напряжения на сопротивление проводников. Поверхностный эффект и эффект близости
Частота напряжения оказывает заметное влияние на величину сопротивления проводников. Это влияние - одно из проявлений так называемого поверхностного эффекта (скин-эффекта). На переменном напряжении плотность тока в приповерхностных слоях проводника оказывается больше, чем плотность тока во внутренних частях проводника. Главная причина скин-эффекта - наличие индуцируемого магнитного поля. Любой проводник с током, в соответствии с законом электромагнитной индукции, создает в окружающем его пространстве и в самом себе магнитное вихревое поле.
Для цилиндрического проводника с круглым сечением силовые линии магнитной индукции имеют вид концентрических окружностей (рисунок 2.6, а). Часть силовых линий пронизывает проводник внутри, часть - окружает его.
Если ток постоянен, то магнитное поле тоже постоянно и не оказывает влияние на общее сопротивление. Если же ток переменный, то порождаемое им переменное магнитное поле, в соответствии с законом электромагнитной
29
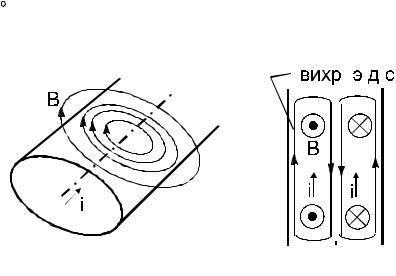
индукции, порождает вихревое электрическое поле с циркуляцией по некоторому контуру L, равной скорости изменения магнитного потока сквозь этот контур:
|
(Edl) = − |
Φ |
|
t |
|||
L |
|
||
|
|
(2.11)
Результирующее поле, получаемое наложением этого вихревого поля и поля, создаваемого внешним источником напряжения, является неоднородно распределенным по сечению проводника. Чтобы понять механизм этого явления, рассмотрим
отрезок |
проводника в про- |
а) |
Рисунок 2.6 |
б) |
|
дольном |
сечении (рисунок |
||||
|
|
|
|||
2.6, б). |
|
|
|
|
Рассмотрим половину периода колебаний тока, в течение которого ток направлен вверх, соответственно силовые линии индукции справа от оси будут входящими, а слева от оси - выходящими из плоскости сечения. При этом первую четверть периода ток увеличивается, то есть di/dt>0, соответственно увеличивается и поток индукции. В соответствии с законом электромагнитной индукции, возникнет такое вихревое электрическое поле, которое будет препятствовать изменению тока в приосевой области проводника (то есть, его увеличению), и, напротив, способствовать его изменению в приповерхностных слоях. Во вторую четверть периода, когда i>0, но при этом di/dt<0, силовые линии вихревого электрического поля изменят направление, и вновь будут препятствовать изменению тока во внутренних частях проводника (то есть уменьшению). В результате получается, что максимальная амплитуда плотности тока имеет место в приповерхностных слоях проводника, а минимальная – во внутренних слоях. Упрощенно скин-эффект можно рассматривать как явление выталкивания линий тока из внутренних областей проводника в приповерхностные области.
Для случая высоких частот, плотность тока в глубине проводника можно считать практически нулевой, по сравнению с плотностью тока в поверхностных слоях. Для сильного скин-эффекта закон изменения плотности тока в зависимости от расстояния х от поверхности имеет вид затухающей экспоненты
j = j0exp(-x/ ), |
(2.12) |
где – параметр, называемый характерной длиной затухания и зависящий от частоты; j0 - плотность тока на поверхности (при х=0).
30
