
- •1.1 Краткий исторический обзор
- •1.2 Математические методы и моделирование экономических процессов
- •1.3 Этапы математического моделирования
- •1.4 Классификация математических моделей
- •Вопросы для самопроверки
- •Тема 2. Модели производства
- •2.1 Производственные функции
- •2.1.1 Понятие производственной функции одной переменной
- •2.1.3 Формальные свойства производственных функций
- •2.1.4 Характеристики производственной функции
- •2.2 Задача производителя
- •2.3 Учет налогов
- •2.4 Функции спроса на ресурсы
- •2.5 Модели ценообразования
- •Вопросы для самопроверки
- •Тема 3. Функция полезности
- •3.1. Множество благ
- •3.2. Функция полезности и ее свойства
- •3.3. Предельная полезность и предельная норма замещения благ
- •3.4. Оптимальный выбор благ потребителем
- •3.4.1. Модель задачи оптимального выбора
- •3.5. Взаимная задача к задаче оптимального выбора благ потребителем
- •Вопросы для самопроверки
- •Тема 4. Балансовые модели
- •4.2 Экономико-математическая модель межотраслевого баланса
- •4.3 Коэффициенты прямых и полных материальных затрат
- •4.4 Агрегирование показателей межотраслевого баланса
- •4.5 Анализ экономических показателей
- •4.5.1 Модель затрат труда
- •4.5.2 Модель фондоемкости продукции
- •4.6. Динамическая модель межотраслевого баланса
- •Вопросы для самопроверки
- •Тема 5. Моделирование финансовых операций
- •5.1. Наращение и дисконтирование
- •5.1.1 Проценты и процентные ставки
- •5.1.2 Наращение по простым процентам
- •5.1.3. Сложные проценты
- •5.1.4. Номинальная и эффективная ставки процентов
- •5.1.6. Учет инфляции при наращении процентов
- •5.1.7. Эквивалентность простых и сложных процентных ставок
- •5.1.8. Дисконтирование и наращение по учетной ставке
- •5.1.9. Наращение по учетной ставке
- •5.1.10. Сравнение методов наращения
- •5.1.11. Сравнение методов дисконтирования
- •5.2. Потоки платежей, ренты
- •5.2.1. Основные определения
- •Ренты бывают постоянные и переменные.
- •5.3. Наращенная сумма потока платежей
- •5.3.1. Наращенная сумма годовой ренты
- •5.3.2.Наращенная сумма годовой ренты с начислением процентов m раз в год
- •5.4. Современная величина потока платежей
- •5.4.1. Современная величина годовой ренты
- •5.4.2. Современная величина годовой ренты с начислением процентов m раз в год
- •5.4.3. Современная величина p – срочной ренты ( m = 1)
- •5.4.4. Современная величина p – срочной ренты при начислении процентов m раз в год
- •5.5 Доходность финансовой операции
- •5.5.1. Различные виды доходности операций
- •5.5.2. Учет налогов и инфляции
- •5.5.3. Поток платежей и его доходность
- •5.5.4. Мгновенная доходность
- •5.6. Кредитные расчеты
- •5.6.1. Показатель полной доходности финансово-кредитной операции
- •5.6.2. Баланс финансово-кредитной операции
- •5.6.3. Определение полной доходности ссудных операций с удержанием комиссионных
- •5.6.4. Методы сравнения и анализа коммерческих контрактов
- •5.6.5. Планирование погашения долгосрочной задолженности
- •Вопросы для самопроверки
- •Тема 6. Математическое и компьютерное моделирование
- •6.1. Классификация видов моделирования
- •6.2. Достоинства и недостатки имитационного моделирования
- •6.3. Типовые задачи имитационного моделирования
- •6.4. Социально-экономические процессы как объекты моделирования
- •6.5. Примеры задач имитационного моделирования
- •Вопросы для самопроверки
- •Тема 7. Сущность метода имитационного моделирования
- •7.1. Метод имитационного моделирования и его особенности
- •7.2. Процесс имитации
- •7.3. Формулирование модели
- •7.4. Оценка адекватности модели
- •7.5. Экспериментирование с использованием имитационной модели
- •7.6. Понятие о модельном времени. Механизм продвижения модельного времени
- •7.7. Интерпретация и реализация результатов моделирования
- •Вопросы для самопроверки
- •Тема 8. Имитационная модель глобальной системы
- •8.1. Основные компоненты динамической мировой модели
- •8.2. Концепция «петля обратной связи»
- •8.3. Основные петли «обратных связей» в мировой модели
- •8.4. Основные переменные в мировой модели
- •8.5. Структура модели мировой системы
- •8.6. Основные результаты экспериментов на модели мировой системы
- •Вопросы для самопроверки
- •Тема 9. Метод Монте-Карло и проверка статистических гипотез
- •Тема 10. Моделирование случайных событий
- •10.1. Моделирование простого события
- •10.2 Моделирование полной группы несовместных событий
- •10.3 Моделирование дискретной случайной величины
- •10.4 Моделирование непрерывных случайных величин
- •10.4.1. Метод обратной функции
- •10.4.2. Моделирование случайных величин с показательным распределением
- •10.4.3. Моделирование случайных величин с равномерным распределением на произвольном интервале (a, b)
- •10.4.4 Моделирование случайных величин с нормальным распределением
- •10.4.5. Моделирование случайных величин с усеченным нормальным распределением
- •10.4.6 Моделирование случайных величин с произвольным распределением
- •Вопросы для самопроверки
- •Тема 11. Системы массового обслуживания
- •11.1. Основные понятия. Классификация СМО
- •11.2 Понятие марковского случайного процесса
- •11.3 Потоки событий
- •11.4. Уравнения Колмогорова. Предельные вероятности состояний
- •11.5. Процесс гибели и размножения
- •11.6. CMО с отказами
- •11.7. СМО с ожиданием (очередью)
- •Вопросы для самопроверки
- •Тема 12. Модели управления запасами
- •12.1. Основные понятия
- •12.2. Статическая детерминированная модель без дефицита
- •12.3. Статическая детерминированная модель с дефицитом
- •12.4. Стохастические модели управления запасами
- •12.5. Стохастические модели управления запасами с фиксированным временем задержки поставок
- •Вопросы для самопроверки
- •ЛИТЕРАТУРА
31
Тема 3. Функция полезности
Основными участниками процесса производства, распределения и потребления благ являются отдельные потребители и производители. Каждый из них имеет свои интересы. Построим теорию поведения потребителя.
3.1. Множество благ
|
Пусть на рынке благ индивидуальному потребителю предлагается n различных |
|||||||||
благ. |
Под набором благ будем понимать совокупность неотрицательных чисел x |
,..., x , |
||||||||
|
|
|
|
|
|
|
|
|
1 |
n |
где |
x j – количество |
j -го блага ( xj |
0, |
j 1,..., n ). Такой набор неотрицательных |
||||||
чисел можно рассматривать как |
n -й вектор |
x (x1,..., xn ) благ. Всевозможные наборы |
||||||||
благ образуют множество благ |
|
|
|
|
|
|
||||
|
R |
n |
x (x ,..., x ); |
x |
|
0, j 1,..., n , |
(3.1) |
|||
|
|
j |
||||||||
|
|
|
1 |
n |
|
|
|
|
||
которое геометрически представляет собой неотрицательный ортант n -го пространства.
Для каждого блага |
j |
заданы ограничения |
|
|
||||||
|
|
x |
min |
x |
|
x |
max |
, |
j 1,...,n . |
(3.2) |
|
|
j |
j |
j |
||||||
|
|
|
|
|
|
|
|
|||
Поэтому, множество наборов благ это ограниченное множество G |
в n -ом пространстве |
|||||||||
G x (x |
,..., x ); |
x |
min |
x |
|
x |
max |
, |
j 1,..., n . |
|
j |
j |
j |
||||||||
1 |
n |
|
|
|
|
|
Множество наборов благ может быть и неограниченным. В этом случае его можно
представить как |
|
|
|
|
|
|
|
|
|
|
|
|
|
xmin |
|
||
G |
|
x (x |
,..., x ); |
x |
j |
, |
j 1,..., n |
|
|
|
1 |
n |
|
j |
|
|
|
или |
|
|
|
|
|
|
|
|
G x (x1 |
,..., xn ); |
x j |
max |
, |
j 1,..., n , |
|||
x j |
||||||||
(3.3)
(3.4)
(3.5)
min |
max |
могут выполняться не для всех j . |
при этом неравенства xj xj |
или xj xj |
|
В распоряжении потребителя имеется ограниченное количество денежных средств |
||
M (доход), которые он может использовать для приобретения благ. Блага приобретаются |
||
по ценам, которые устанавливаются рынком и не зависят от отдельного потребителя.
Обозначим их p1, p2 ,..., pn |
соответственно для 1-го, 2-гобюююб n -го блага. Вектор |
|
p ( p1, p2 ,..., pn ) называют вектором цен благ, при этом |
p j 0, j 1,..., n . Тогда |
|
|
n |
|
стоимость набора благ равна |
pT x p j xj . |
|
|
j 1 |
|
Стоимость набора благ для потребителя не превосходит его дохода M , т.е. |
||
|
n |
|
|
p j xj M . |
(3.6) |
|
j 1 |
|
Неравенство (3.6) называют бюджетным ограничением. |
|
|
Неравенство (3.6) вместе с |
неравенством (3.2) определяет |
множество K доступных |
наборов благ на рынке товаров и услуг. В силу наличия бюджетного неравенства (3.6) множество K всегда будет ограниченным множеством Rn .
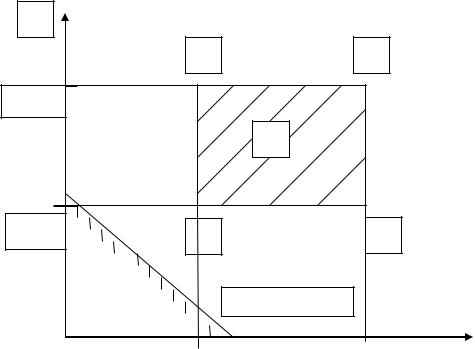
32
Например, в случае множества |
G , заданного неравенствами вида (3.2), получаем, |
что множество K |
доступных благ может быть одним из трех: |
|
|
|
|
|
|
|
1) пустое множество, т.е. при имеющемся доходе |
M |
и ценах |
p ( p |
, p |
,..., p |
n |
) |
|
|
|
|
1 |
2 |
|
|
||
потребитель не может приобрести на рынке даже минимального набора благ и можно сказать, что в этом случае он живет за чертой бедности;
2) часть n -мерного параллелепипеда G , т.е. потребителю доступны не все наборы благ при имеющемся доходе M и установившихся ценах p на рынке благ;
3) весь n -мерный параллелепипед G , т.е. потребитель настолько богат, что ему доступен любой набор благ при его доходе и действующих ценах.
На рис. 3.1. изображены эти случаи при n 2 .
x2 |
|
|
|
B |
C |
x2max |
|
|
|
|
GG |
x2min |
A |
D |
|
|
p1x1 + p1x1 = M |
|
|
|
|
|
|
x1min |
|
x1max |
|
x1 |
|
Рис. 3.1а. Пустое множество доступных благ
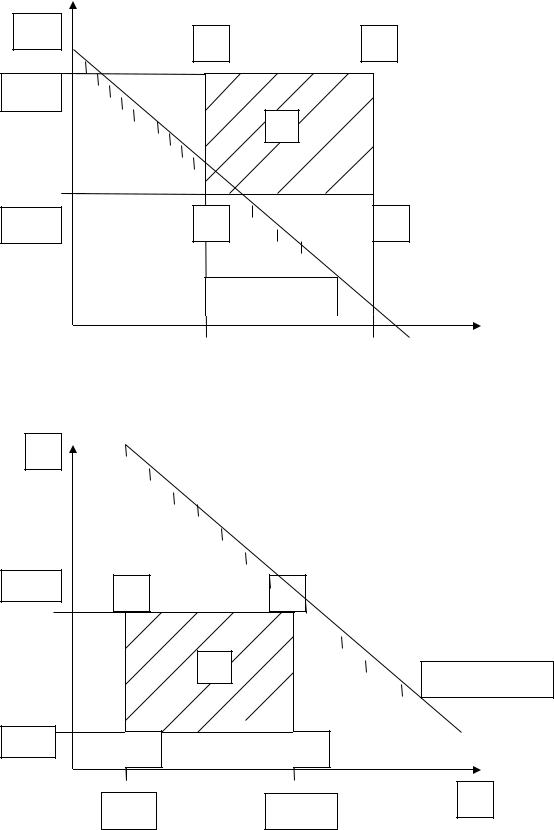
33
x2 |
B |
C |
|
||
x2max |
|
|
|
|
G |
x2min |
A |
D |
p1x1 + p1x1 = M
|
|
|
|
|
|
|
|
x1min |
|
|
x1max |
|
x1 |
||
Рис. 3.1б. Частичное множество доступных благ
x2
x2max |
B |
C |
|
||
|
|
G |
x2min |
A |
D |
|
||
|
x1min |
x1max |
p1x1 + p1x1 = M
x1
Рис. 3.1в. Полное множество доступных благ

34
Таким образом, множество определяемым системой неравенств
K
доступных благ является выпуклым множеством,
x |
|
x |
min |
, |
|
j |
j |
||||
|
|
|
j
J1
,
x |
|
x |
max |
, |
|
j |
j |
||||
|
|
|
j
J |
2 |
|
,
n |
|
p j xj |
M |
j 1 |
|
,
(3.7)
где
J |
1 |
, J |
2 |
|
|
– некоторые подмножества множества |
J 1, 2,..., n . |
3.2. Функция полезности и ее свойства
Рассмотрим вопрос о выборе набора благ. Каждое благо должно удовлетворять ту или иную потребность. Способность удовлетворять ту или иную потребность называют
полезностью блага.
Потребитель при рассмотрении двух наборов благ принимает одно из следующих решений:
x (x |
,..., x |
) |
1 |
n |
|
и
y ( y |
,..., y |
n |
) |
1 |
|
|
а) набор б)набор
x
y
предпочтительнее (полезнее), чем набор предпочтительнее, чем набор x ;
y
;
|
в) наборы |
|
Запись x |
x |
и набор y |
чем набор y .
x и |
y равнозначны (равноценны, одинаково полезны). |
|
|
|
y |
означает, что набор x предпочтительнее набора |
y ; запись |
x |
y – набор |
равнозначны; запись x y означает, что набор x |
не менее предпочтителен, |
|||
Введенное понятие отношения предпочтения позволяет сформулировать следующий принцип выбора потребителя: потребитель выбирает наиболее предпочтительный набор среди всех
доступных ему наборов благ. |
|
|
Вместо рассуждений на основе заданного отношения предпочтения |
используем |
|
функцию полезности для предпочтения одного набора благ другому. |
|
|
Функция
u(x)
u(x |
,..., |
1 |
|
xn
)
, определенная на неотрицательном ортанте
Rn
(или
некотором |
n |
G R |
|
|
|
предпочтения , если
), называется
u(x) u( y)
функцией полезности, соответствующей отношению
, тогда и только тогда, когда x y ,
причем если
u(x)
u( y)
, то
x |
y |
и обратно, если
x
y
, то
u(x)
u( y)
.
Функция полезности u(x) , по существу, представляет систему предпочтений
потребителя. если u(x)
Основное ее свойство в том, потребитель предпочитает выбирать |
x , а не y , |
u( y) , она упорядочивает наборы по предпочтению их друг другу. Отсюда
следует, что потребитель при выборе набора благ стремится максимизировав свою функцию полезности.
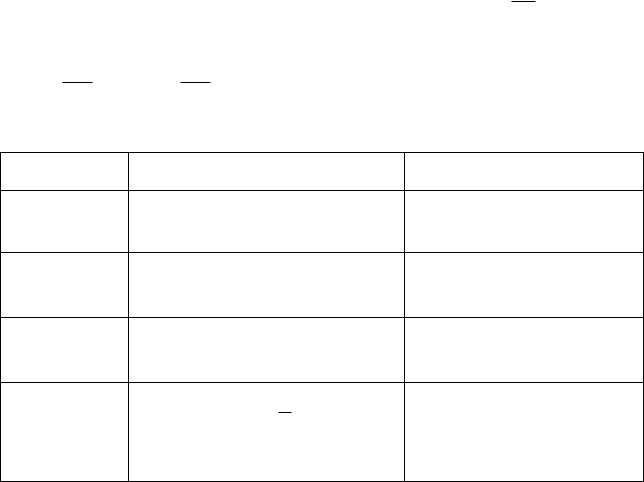
В таблице 3.1 приведены четыре типа функции полезности. Рассмотрим некоторые общие свойства функции полезности.
1)Функция полезности и дважды дифференцируема и строго выпукла.
2)Функция полезности не насыщена. Свойство ненасыщаемости состоит в том, для
любых заданных двух наборов |
x, y RN |
соотношение x y влечет u(x) u( y) , а |
|
соотношения x y |
|
|
|
и x y влекут |
u(x) u( y) . Значит, функция полезности |
||
35
является возрастающей по любому ее аргументу, т.е.
3) |
lim |
u |
, |
lim |
u |
0, |
j 1,..., n . |
||
x |
|
|
|
||||||
|
x j 0 |
j |
|
x j x |
j |
|
|
||
|
|
|
|
|
|
|
|
||
u(x) |
0, |
j 1, n, |
|
x |
|
||
j |
|
|
|
|
|
|
|
x
Rn
.
Таблица 3.1
Тип функции полезности
Логарифмичесчкая
Мультипликативная
Аддитивная
Квадратичная
Функция полезности
|
n |
|
|
|
|
|
|
|
|
|
|
u(x) a j |
ln x j |
|
|
|
|
|
|||||
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
u(x) a x j |
j |
|
|
|
|
|
|
||||
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u(x) j x j |
j |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
1 |
n |
n |
|
|
u(x) |
|
a |
x |
|
|
|
|
b |
x x |
|
|
j |
|
|
|
j |
|||||||
|
j |
|
|
|
2 |
ij |
i |
||||
|
j 1 |
|
|
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ограничения
a |
j |
0, |
x |
j |
1, |
j 1,..., n |
|
|
|
|
|
0 |
j |
1, |
|
x |
j |
0, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
j 1,..., n, |
a 0. |
|
|
|
|
|||||||
0 |
j |
1, |
x |
j |
0, |
j |
0, |
|||||
|
|
|
|
|
|
|
||||||
j 1,..., n. |
|
|
|
|
|
|
|
|
|
|||
|
|
n |
|
|
|
|
|
|
|
|
|
|
aj bij xi |
0, j 1, n |
|||||||||||
|
i 1 |
|
|
|
|
|
|
|
|
|
||
B 0 |
|
|
|
|
|
|
(отрицательно |
|||||
определена)
В ортанте
Rn
уравнению
u(x)
c
, где
c
– константа, соответствует определенная
поверхность равноценных (одинаковой полезности) наборов благ (множество безразличия), и наоборот, каждому множеству безразличия соответствует некоторая
поверхность, определяемая уравнением
u(x)
c
.
Эти поверхности называют
поверхностями безразличия. В случае двух благ, т.е. в безразличия.
R2
их называют кривыми
Для данной функции полезности кривые (поверхности) безразличия обладают следующими свойствами:
1)через каждую точку множества товаров проходит лишь одна кривая (поверхность) безразличия;
2)линии (поверхности) безразличия не пересекаются, причем кривая, лежащая выше
иправее другой кривой, представляет собой более предпочтительные наборы товаров;
3)линии (поверхности) безразличия обращены выпуклостью к началу координат (вытекает из строгой вогнутости функции полезности);
4) множество наборов x , для которых является выпуклым множеством.
u(x) c
(предпочтительное множество)
