Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математическое и имитационное моделирование экономических процессов..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

5.16 Mб

Скачать

☆

<<< < Предыдущая 26 27 28 29 30 31 32 33 34 35 36 37 3839 / 5039 40 41 42 43 44 45 46 47 48 49 50 > Следующая >>>

140

моделировании дискретных случайных величин фактически используется та же процедура, что и при моделировании ПГНС.

10.4 Моделирование непрерывных случайных величин

10.4.1. Метод обратной функции
Пусть имеется некоторая непрерывная случайная величина		x , заданная функцией
распределения	F(x) . Можно доказать, что значения этой	функции		равномерно
распределены в интервале (0,1). Поэтому между случайной величиной			z ,	равномерно
распределенной в том же интервале, и функцией распределения случайной величины x
существует взаимно однозначное соответствие, т. е.
	z F(x) .			(10.1)
Отсюда следует,
	x F 1(z) .			(10.2)

Следовательно, если уравнение (2.1) имеет аналитическое решение, то для

моделирования случайной величины	x		можно использовать								датчик случайных чисел,
генерирующий величину z , и затем осуществить расчет по формуле (2.2).
10.4.2. Моделирование случайных величин с показательным распределением
Пусть имеется случайная величина			x	с		показательным					распределением. Функция
распределения имеет вид:
	F ( x)				1 e		x		,
	F ( x)				1 e				,
где – параметр распределения.
Применив метод обратной функции, получим:
z F (x) 1 e								x		,
z F (x) 1 e										,
откуда
x		1	ln(1 z) .								(10.3)
x			ln(1 z) .								(10.3)

Учитывая, что случайная величина		(1 z) имеет также равномерное распределение в
интервале (0,1), соотношение (10.3) можно заменить соотношением
	x			1		ln(z) .
	x					ln(z) .

Экспоненциальный закон распределения применяют для моделирования следующих явлений:

времени поступления заказа на предприятие;

посещения покупателями магазина супер-маркета;

времени телефонных разговоров;

срока службы деталей и узлов в компьютере.

На первый взгляд, это распределение является надуманным. Поэтому рассмотрим предельную теорему о суперпозиции потоков. Предположим, что можно наблюдать k независимых потоков событий (рис. 10.4)

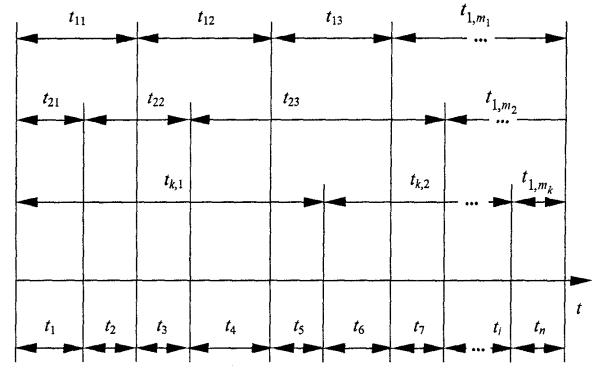
141

Рис. 10.4

В каждом таком потоке можно наблюдать m j элементарных событий ( j 1,...,k

Интервалы между tkj событиями — это независимые случайные величины,

распределенные по по неизвестному закону с математическим ожиданием j . Спроектируем моменты всех событий на общую ось времени и рассмотрим случайный

интервал времени

t T (k)

между двумя событиями полученного суммарного потока,

	k		j
состоящего из n событий , где n		m	j	.
состоящего из n событий , где n		m		.
	j 1
Теорема. Если сделать предельный переход и устремить					n , то распределение
случайной величины интервала t T (k)			в суммарном потоке событий, состоящем из

элементарных потоков, устремится к экспоненциальному закону с математическим ожиданием

M (t)

k j

j 1

Следствие. Поток заявок, интервал поступления которых в некую систему имеет экспоненциальное распределение, является простейшим.

Пример 10.1. Допустим, что имеется некая крупная фирма. Клиенты фирмы - это физические и юридические лица. Каждый из них может иметь набор планов и расписанных дел на значительном интервале времени. Однако если рассмотреть суммарный поток обращений этих клиентов к служащим фирмы по разным вопросам, то интервал времени между двумя последовательными обращениями в соответствии с рассмотренной теоремой является случайной величиной, распределенной по экспоненциальному закону.

10.4.3. Моделирование случайных величин с равномерным распределением на произвольном интервале (a, b)

142

Датчик случайных чисел генерирует случайные величины с равномерным распределением в интервале (0,1). Если же нужно моделировать случайные величины с равномерным распределением в интервале (a,b) то можно воспользоваться методом обратной функции.

Для рассматриваемого случая выражение (2.1) примет вид:

z F (x) x a , b a

Откуда

z(b a)

На практике применяется и другой способ Вместо границ интервала задаются среднее

задания	равномерного распределения.
значение	случайной величины	xcp	и

величина интервала x . Тогда определение возможного значения случайной величины с равномерным распределением может быть произведено по формуле

x xcp

x(z

0,5)

Равномерное распределение можно использовать при расчетах по сетевым графикам работ, в военном деле (времени выдвижения воинской части или ее подразделения на исходный рубеж, времени марша)

10.4.4 Моделирование случайных величин с нормальным распределением

Метод обратной функции для нормального распределения неприменим, так как после подстановки соответствующей функции распределения выражение (2.2) не имеет аналитического решения. Поэтому в данном случае применяется другой метод.

Согласно центральной предельной теореме теории вероятностей при сложении достаточно большого числа одинаково распределенных независимых случайных чисел получается случайная величина, имеющая нормальное распределение.

Как показали исследования, уже при сложении более десяти случайных величин с равномерным распределением в интервале (0,1) получается случайная величина, которая с точностью, достаточной для большинства практических задач, может считаться распределенной нормально.

Процедура розыгрыша нормально распределенной случайной величины заключается в следующем.

1.Сложим 12 случайных величин с равномерным распределением в интервале (0,1), т. е. составим сумму

i 1

Использовав известные теоремы о сумме математических ожиданий и дисперсий независимых случайных величин, можно установить, что в данном случае случайная величина v имеет следующие характеристики:

математическое ожидание:

12			1
M (v) M (zi ) 12			1	6 ;
M (v) M (zi ) 12				6 ;
i 1	2
i 1
дисперсия:
12		1
D(v) D(zi ) 12		1		1 .
D(v) D(zi ) 12	12			1 .
i 1	12
i 1

	143
среднее квадратическое отклонение:	(v)	D(v) 1.

2. Нормируем и центрируем случайную величину v , т. е. перейдем к величине

		v M (v)	v 6.
		(v)

2.От нормированной и центрированной величины перейдем к случайной

	величине y с заданными параметрами M ( y) и ( y) по формуле
	y M ( y) ( y) ,
где	M ( y) – известное математическое ожидание случайной величины	y	; ( y)	–
известное среднее квадратическое отклонение случайной величины		y .

Любые сложные работы на объектах экономики (ввод информации из документа в компьютер, проведение переговоров, ремонт оборудования и др.) состоят из многих коротких последовательных элементарных составляющих работ. Причем количество этих составляющих настолько велико, что условие выполнимости центральной предельной теоремы не вызывает сомнений. Поэтому при оценках трудозатрат всегда справедливо предположение о том, их продолжительность — это случайная величина, которая распределена по нормальному закону.

10.4.5. Моделирование случайных величин с усеченным нормальным распределением

Усеченное

нормальное распределение

случайной

величины x

задается четырьмя

параметрами: математическим ожиданием M (x) ,

средним квадратическим отклонением

(x) , а также минимальным и максимальным значениями

x1 и

(точками усечения).

Функция распределения случайной величины

определяется равенством

x x

;

F (x)

(t)

)] A,

;

[

x x

x M (x)

M (x)

x M (x)

где

; t

;

; t

0 (t2 ) 0 (t1)

(x)

Существуют также формулы для расчета математического ожидания, дисперсии и среднего квадратического отклонения случайной величины x . Однако с достаточной для практики точностью при моделировании случайной величины с усеченным нормальным распределением можно обойтись без расчетов по формулам.

Для определения возможных значений случайной величины с этим распределением можно использовать алгоритм, схема которого приведена на рис. 10.5.

<<< < Предыдущая 26 27 28 29 30 31 32 33 34 35 36 37 3839 / 5039 40 41 42 43 44 45 46 47 48 49 50 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

10.4 Моделирование непрерывных случайных величин

10.4.1. Метод обратной функции

10.4.2. Моделирование случайных величин с показательным распределением

10.4.3. Моделирование случайных величин с равномерным распределением на произвольном интервале (a, b)

10.4.4 Моделирование случайных величин с нормальным распределением

10.4.5. Моделирование случайных величин с усеченным нормальным распределением